[Compiler] 3.1. CFG(Context Free Grammars)

CFG는 Context free language를 나타내기 위한 notation이다.
재귀적 형태를 나타내는데 용이하다.

CFG의 구성

• Terminal: 대체될 수 없는 기본 symbol들을 의미한다. 보통, 토큰 이름 == terminal이 된다.
• Non-terminal: 다른 non-terminal이나 terminal로 대체될 수 있는 syntactic variable이다.
• Start symbol: 하나의 non-terminal로, 대개 첫번째 rule의 non-terminal이다.
• Production(→): Non-terminal이 대체될 때의 규칙이다.

CFG 규칙

(통상)

• Non-terminal은 대문자로, terminal은 소문자로 작성한다.
• Non-terminal, terminal, 𝜖을 포함한 일련의 문자열은 $\alpha,\beta,\omega$로 작성한다.

e.g.

Terminal = {+, id, *, (, )} 일 때,
e.g., $id+id, id*id, (id), id+id*id,(id+id)*id$ 등을 나타내는 CFG는 다음과 같이 나타내질 수 있다.
$E\rarr E+E|E*E|(E)|id$

Derivation

• derivation($\Rarr$)은 replacement를 나타낸다.
• $\Rarr ^*$는 0번 이상의 derivation을 나타낸다.
• $\Rarr _{lm}$ 은 가장 왼쪽의 non-terminal부터 대체한다.
• $\Rarr _{rm}$ 은 가장 오른쪽의 non-terminal부터 대체한다.

예를 들어, $E\rarr E+E|E*E|(E)|id$ 에 대해 $id*id+id$ 를 만들어보자

• left-most derive
  $E\Rarr _{lm}E+E\Rarr _{lm}E*E+E\Rarr _{lm}id*E+E\Rarr _{lm}id*id+E\Rarr _{lm}id*id+id$
  $E\Rarr _{lm} ^* id*id+id$
• right-most derive
  $E\Rarr _{rm}E+E\Rarr _{rm}E+id\Rarr _{rm}E*E+id\Rarr _{rm}E*id+id\Rarr _{rm}id*id+id$
  $E\Rarr _{rm} ^* id*id+id$

Token validation test

• CFG $G$의 start symbol $A$에 대해, $A\Rarr ^*\alpha$라면 $\alpha$는 $G$의 sentinel form이다.
• sentinel form $\alpha$가 terminal으로만 이루어졌다면 $\alpha$는 $G$의 sentence form이다.
• $L(G)$는 CFG $G$의 language이다. ($L(G)=\{\alpha|\alpha \text{ is sentence of }G\}$)

(token 집합 등의) 입력 문자열이 $L(G)$에 포함된다면, 입력이 $G$에 대해 valid하다고 할 수 있다.

좋은 CFG의 조건

1. 모호성이 없다
2. left recursion이 없다
3. 각각의 non-terminal에 대해, 특정 input symbol로 부터 단 하나의 production만 선택 가능하다.

모호성 제거

$E\rarr E+E|E*E|id$ 에 대해, id*id+id를 나타내는데 다음 두가지 모두 가능하다.

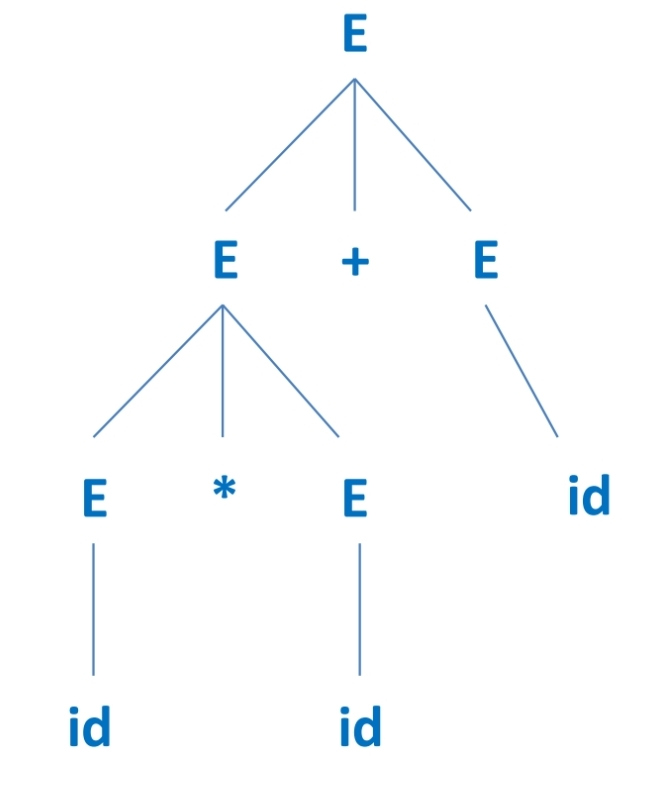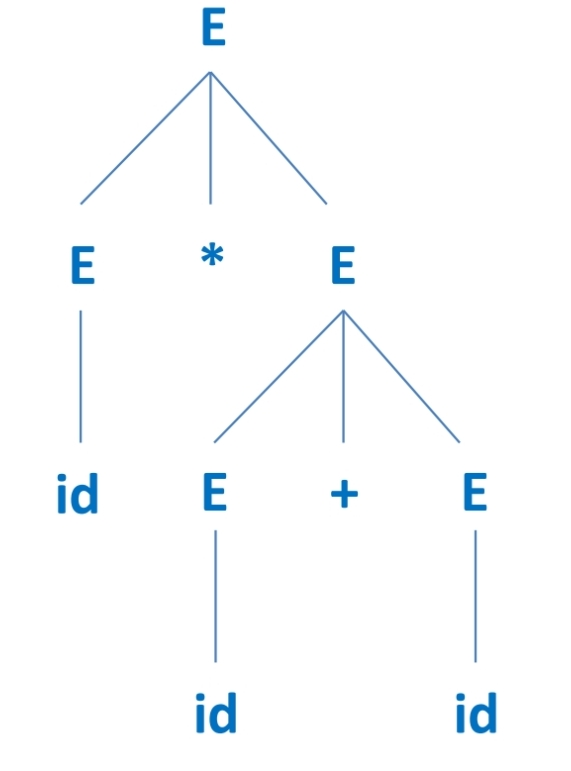위와 같이 여러 tree로 나타낼 수 있는 CFG는 비효율적이다.
*가 +보다 더 높은 우선순위를 가진다는 것을 명시하면, 모호성이 제거된다.
$E\rarr T+E|T$
$T\rarr F*T|F$
$F\rarr(E)|id$

Left-recursion 제거

$A\Rarr ^+ A\alpha$ ($A$: nonterminal, $\alpha$: non-terminal&terminal로 이루어진 모둔 sequence) 를 포함한 문법을 left recursive grammar라고 한다.
e.g. $S\rarr Aa|b, A\rarr Sb$
$S \Rarr Aa \Rarr Sba$
$S=A$, $ba = \alpha$ 로 보면, left recursion 형태임을 알 수 있다.

이를 해결하기 위해, left-recursion을 $S\rarr bA, A\rarr aA|\epsilon$ 형태의 right recursion으로 변환할 수 있다.

e.g. $S\rarr S\alpha_1|S\alpha_2|\dots|S\alpha_m|\beta_1|\beta_2|\dots|\beta_n$

1. 새로운 non-terminal $A$를 만들고, 모든 $\alpha_i$에 대해 production rule $\alpha_i A$를, 그리고 $\epsilon$을 추가한다.
   $A\rarr\alpha_1A|\alpha_2A|\dots|\alpha_nA|\epsilon$
2. non-terminal $S$에 대해, 모든 $\beta_i$에 대한 $\beta_iA$ production rule을 추가한다.
   $S\rarr\beta_1A|\beta_2A|\dots|\beta_nA$

단일 선택 보장: Left factoring

$E\rarr T+E|T, T\rarr F*T|F, F\rarr (E)|id$
의 경우, 첫번째에서 $T$가 중복, 두번째에서 $F$가 중복되는 것을 볼 수 있다.
이 모호성을 제거하기 위해, left factoring을 적용할 수 있다.

1. non-terminal $A$에 대해, 가장 긴 공통 접두사 $\alpha$를 찾는다.
   $E$에 대해, $\alpha = T$
2. $A\rarr \alpha\beta$ 형태의 모든 production을 $A\rarr\alpha A'$으로 대체한다.
   $E\rarr TE'$
3. 2에서 대체된 production에 대해, $A'\rarr\beta$ 형태의 새로운 production을 추가한다.
   $E'=+E|\epsilon$
4. 모든 non-terminal에 대해 더이상 공통 접두사가 없을때까지 1-3을 반복한다.
   $E\rarr TE', E'=+E|\epsilon$
   $T\rarr FT', T'\rarr*T|\epsilon$
   $F\rarr (E)|id$

AST(Abstract Syntax Tree)

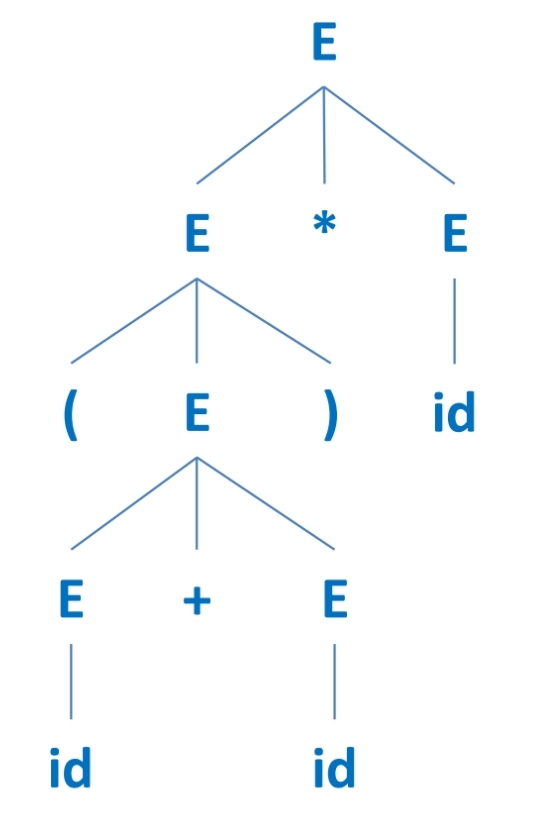
다음 parse tree에서, 할 수 있는 추상화 작업은 다음과 같다

1. Single-successor node
   
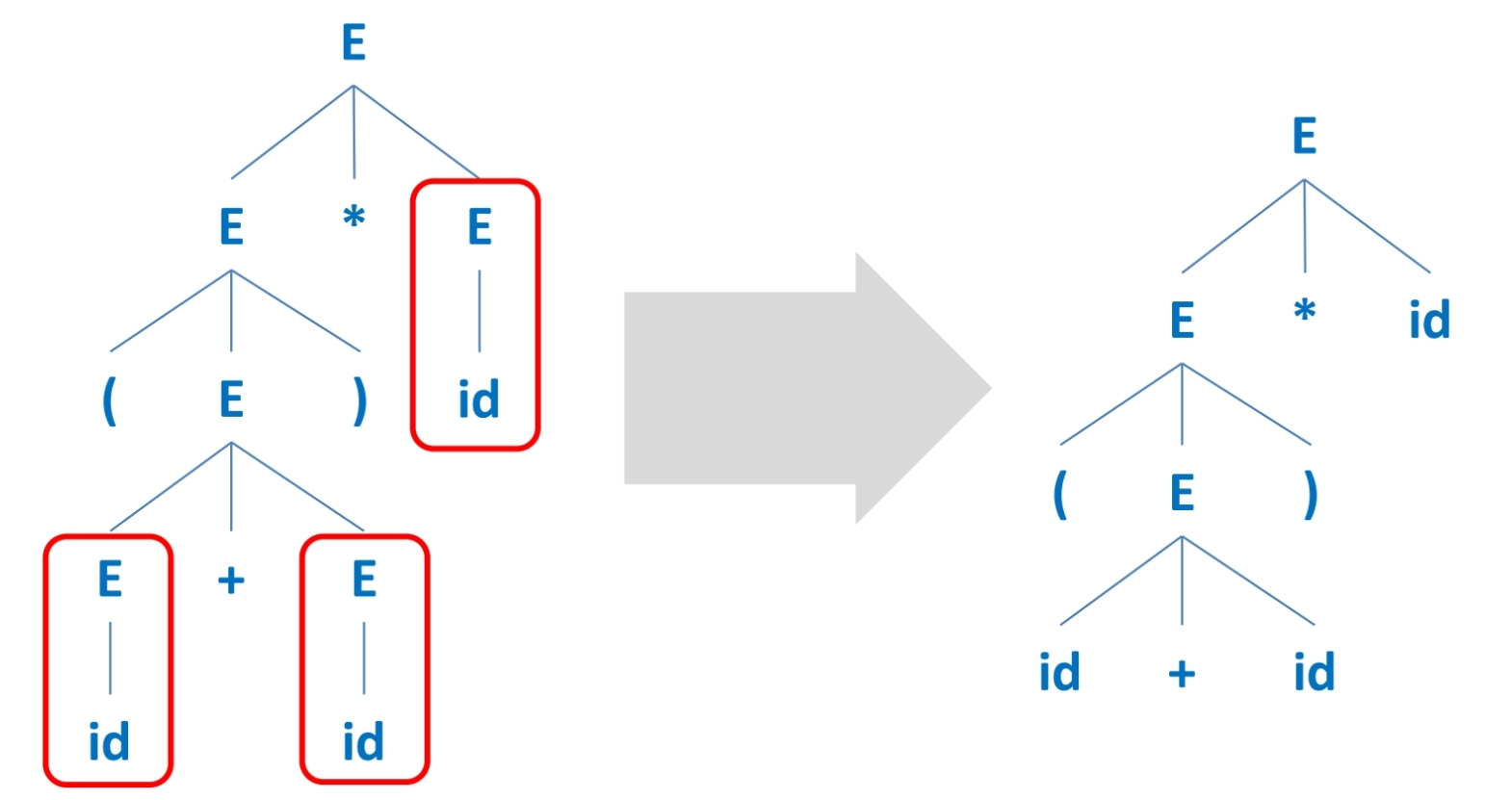
   자식을 하나만 가지는 노드를 자식 노드 하나로 합친다.

2. 문법적 디테일 (괄호, 콤마 등)
   
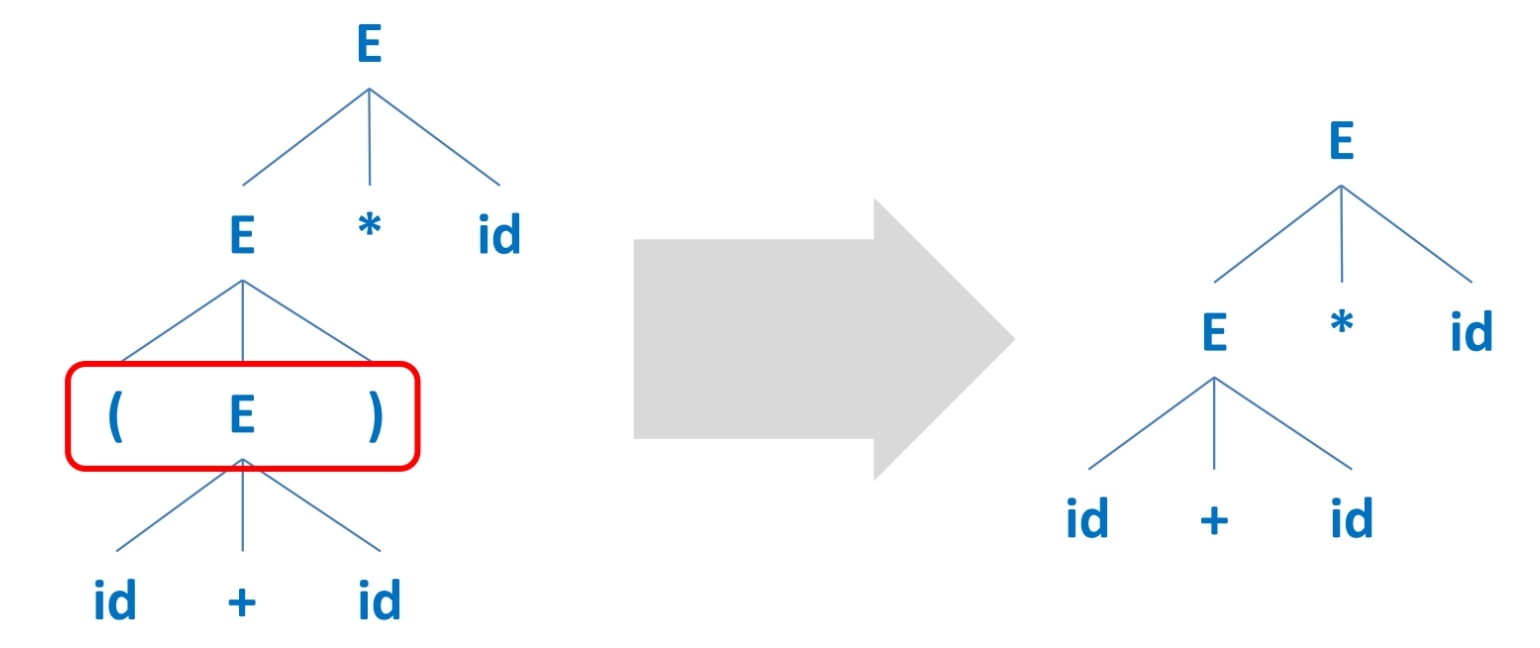
   parse tree가 이미 문법적 디테일을 설명해주기 때문에, 제거해도 된다.

3. 연산자를 자식으로 가지는 non-terminal
   

AST Construction

문법적 production과 관련된 액션인 Semantic action을 만든다.
e.g. CFG $G$ : $E\rarr E+E|E*E|(E)|id$

Production	Semantic action
$E\rarr E_1+E_2$	E.node = new Node('+', E1.node, E2.node)
$E\rarr E_1*E_2$	E.node = new Node('*', E1.node, E2.node)
$E\rarr (E_1)$	E.node = E1.node
$E\rarr id$	E.node = new Leaf(id, id.value)