[CS224n] Lect.1 : Introduction and Word Vectors

The course

• Prof. Christopher Manning
• 학습 목표 :
  1. 효과적, 현대적인 딥러닝 방법론 이해
     • RNN, 어텐션 등 NLP의 핵심 방법론
  2. 자연어에 대한 큰그림, 자연어를 이해하는 것과 생성하는 것의 난관을 이해
  3. NLP 문제를 이해하고 이를 해결할 시스템을 작성할 수 있는 능력 배양
     • 단어의 의미, 의존성 파싱, 기계번역, 질의응답 등
• 올해 다른 점:
  • charater models, transformers, safety/fairness, multitask learn 등의 내용을 다룸
  • 과제 많음
  • Tensorflow보다 Pytorch 활용

Human language and word meaning

• 2가지 일화

  • XKCD 만화

    • 원본
    • 많은 학생들이 언어를 형식적으로 이해하려 함 (형식언어)
    • 그러나 인간 언어는 복잡하고 다목적임
    • 언어는 혼란스러운 시스템으로, 청중마다 해석이 다름
    • 언어의 의미는 불확실하지만 소통이 가능함
    • 정보 전달 외에도 사회적 기능이 중요함

  • 도서관 사진

    • 원본
    • 인간의 지식은 주로 언어로 전달됨
    • 얀 르쿤은 인간과 오랑우탄의 지능 차이를 작게 보지만, 강연자는 반대 입장임
    • 오랑우탄은 뛰어난 도구 사용 능력을 가짐
    • 언어는 약 10만 년 전에 등장해 인간의 협력을 강화함
    • 글쓰기는 약 5,000년 전 발명되어 지식을 공간적·시간적으로 전파하게 함
    • 언어는 인간의 발전을 촉진한 중요한 도구임
    • 인간 언어는 느린 네트워크이며, 정보 전달 속도가 낮음

• 단어의 의미를 어떻게 나타내는가?

  • 사전은 단어의 의미를 설명하지만, 정의가 불완전할 수 있음
  • 언어학에서는 'Denotational Semantics'로 이해되며, 단어가 나타내는 것임
    • 예: '의자'는 여러 의자를 포함함

• 컴퓨터에서 활용가능한 의미를 가지는 방법

  • 컴퓨터에서 단어 의미를 다룰 때는 WordNet 같은 온라인 자원을 사용함
  • WordNet은 단어의 의미와 관계를 설명함 (동의어나 상하관계 등)
  • NLTK : 대다수 태스크에서 좋진 않지만 대체로 가능함
    • 여기에 ‘Good’라는 단어를 넣어봤을때 명사 형용사 등으로 나오고, 뜻도 나옴. 사실상 사전
    • 단어간 관계 같은 것도 파악할 수 있음

• WordNet과 같은 자원의 문제

  • 자원으로서는 좋은데 뉘앙스가 없음, 맥락에 따라 잘못된 말이 선택될 수도 있음
  • 신조어 없음
  • 주관적
  • 사람이 직접 작성하고 적용해야
  • 단어 간 유사성을 정확하게 연산하지 못함

• 전통적 NLP → 단어를 이산 심볼로 나타냄

  • 단어를 사용했음 (Localist Representation)
    • 원핫인코딩 등을 적용해야 했음 → 단어는 접두/접미사에 따라 무한
    • 단어 간 유사성을 파악하는 것은 힘듦
      • ex) motel : 00000100 이고 hotel : 01000000 이면 이 둘은 orthogonal함 (실제로 비슷한데도)
    • 그래서 유사도 테이블을 가지고 있었는데, 단어수가 많아지니까 힘들어짐
  • ⇒ 단어를 벡터로 나타내면 단어간 유사성 계산이 매우 간단해짐

• 단어의 맥락으로 의미를 나타내기

  • Distributional Semantics : 단어의 의미는 자주 함께 나타나는 단어들을 통해 알 수 있다

    You shall know a word by the company it keeps - J.R.Firth 1957

  • 특정 단어의 뜻을 알고 싶으면, 그게 들어간 문장을 엄청 많이 보면 된다

• 단어 벡터

  • 특정 단어를 벡터로 표현을 한다면, 단어의 의미는 그 벡터의 원소들로 표현됨
  • 이를 시각화할 수도 있음 (100차원 이상을 2차원으로 축소한다면!)
  • 생각보다 관계를 잘 나타냄을 볼 수 있음

Word2vec introduction

• Word2Vec는 단어벡터를 배우는 프레임워크
  • 굉장히 많은 텍스트 데이터를 기반으로 함
  • 처음엔 하나의 단어에 랜덤 벡터를 주고, 반복적으로 바꿈
  • 단어가 사용되는 맥락을 예측함

Word2vec objective function gradients

• Word2Vec의 목적함수

  • 단어 하나를 정해서 앞뒤의 단어를 예측함

    $L(\theta) = \prod^T_{t=1} \prod_{\substack{-m\le j \le m\\j\ne 0}} P(w_{t+j} | w_t ; 0)$

  • $L(\theta)$를 likelihood라고 함

    $J(\theta) = -\frac{1}{T} \log L(\theta) = -\frac{1}{T} \sum_{t=1}^{T} \sum_{\substack{-m \leq j \leq m \\ j \neq 0}} \log P(w_{t+j} \mid w_t; \theta)$

  • $J(\theta)$를 목적함수라고 함

    • 로그가 들어가는 것이 중요함 → 곱을 구할 때 로그를 쓰면 보통 좋기 때문
    • 목적함수 최소화가 목적

  • $P(w_{t+j} \mid w_t; \theta)$를 어떻게 구하는데?

    • 각 단어별로 center word일때의 벡터와 context word 일 때의 벡터가 있음
• Word2Vec의 예측함수
  $P(o \mid c) = \frac{\exp(u_o^T v_c)}{\sum_{w \in V} \exp(u_w^T v_c)}$
  • (단어 o와 단어 c의 유사도) / (전체 단어 개수) = 확률
  • 지수함수 씌우면 모두 양수가 돼서 쓰는 것
  • 소프트맥스 함수를 씀 → 하드맥스는 가장 높은 단어의 확률을 증폭하고, 소프트맥스는 작은 단어에도 약간의 확률을 부여함

Optimization basics

• 매개변수를 최적화하여 모델을 훈련함 → 경사면을 내려가듯이

  • 모델을 훈련시키기 위해서는 모든 벡터 그래디언트를 연산해야

    • 모든 단어의 각각 o와 c를 포함하는 아주 긴 벡터를 $\theta$ 로 한다 (모든 단어는 2개 벡터 有)

      $\theta = \begin{bmatrix}v_{\text{aardvark}} \\v_a \\\vdots \\v_{\text{zebra}} \\u_{\text{aardvark}} \\u_a \\\vdots \\u_{\text{zebra}}\end{bmatrix}\in \mathbb{R}^{2dV}$

    • 경사면을 내려가면서 이 파라미터를 최적화함

  • 하려고 하는 것 : 파라미터를 변화시켜서 목적함수를 최소화한다
    • 이때 파라미터는 벡터의 내용

• 최적화 함수 구하기

  $\frac{\partial}{\partial v_c}P(o|c) = \frac{\partial}{\partial v_c} \log \left( \frac{\exp(u_o^T v_c)}{\sum_{w=1}^{V} \exp(u_o^T v_c)} \right)$
  $=\frac{\partial}{\partial v_c} \log \exp(u_o^T v_c) - \frac{\partial}{\partial v_c} \log \left( \sum_{w=1}^{V} \exp(u_o^T v_c) \right)$

                                                   (왼쪽 항은 분자, 오른쪽 항은 분모)

  $(분자)=\frac{\partial}{\partial v_c} u_o^T v_c\\=\frac{\partial}{\partial v_{c1}} (u_{o1}v_{c1} + u_{o2}v_{c2} + ... u_{o100}v_{c100}),\frac{\partial}{\partial v_{c2}} (u_{o1}v_{c1} + u_{o2}v_{c2} + ... u_{o100}v_{c100}) ...\\=u_{o1},u_{o2}...u_{o100}\\=u_o$
  
  

  $(분모) = \frac{\partial}{\partial v_c} \log \left( \sum_{w=1}^{V} \exp(u_o^T v_c) \right)\\= \frac{1}{\sum_{w=1}^{V} \exp(u_w^T v_c)} \cdot \sum_{x=1}^{V}\frac{\partial}{\partial v_c} \exp(u_x^T v_c)\\=\frac{1}{\sum_{w=1}^{V} \exp(u_w^T v_c)} \cdot \sum_{x=1}^{V} \exp(u_x^T v_c) \cdot u_x$
  
  

  $(분자)-(분모)\\= u_o - \sum_{x=1}^{V} \frac{\exp(u_x^T v_c)}{\sum_{w=1}^{V} \exp(u_w^T v_c)}\cdot u_x\\= u_o - \sum_{x=1}^{V} p(x|c)\cdot u_x$

  ⇒ 다차원에서의 기울기 값인데, 실제 관찰된 context word($u_o$)에서 모델이 추정한 값을 뺌

  (모델이 추정한 값 = 각 단어의 값 $\times$ 그것의 확률) (⇒가중평균)

  ⇒ 전형적인 손실함수 꼴
  

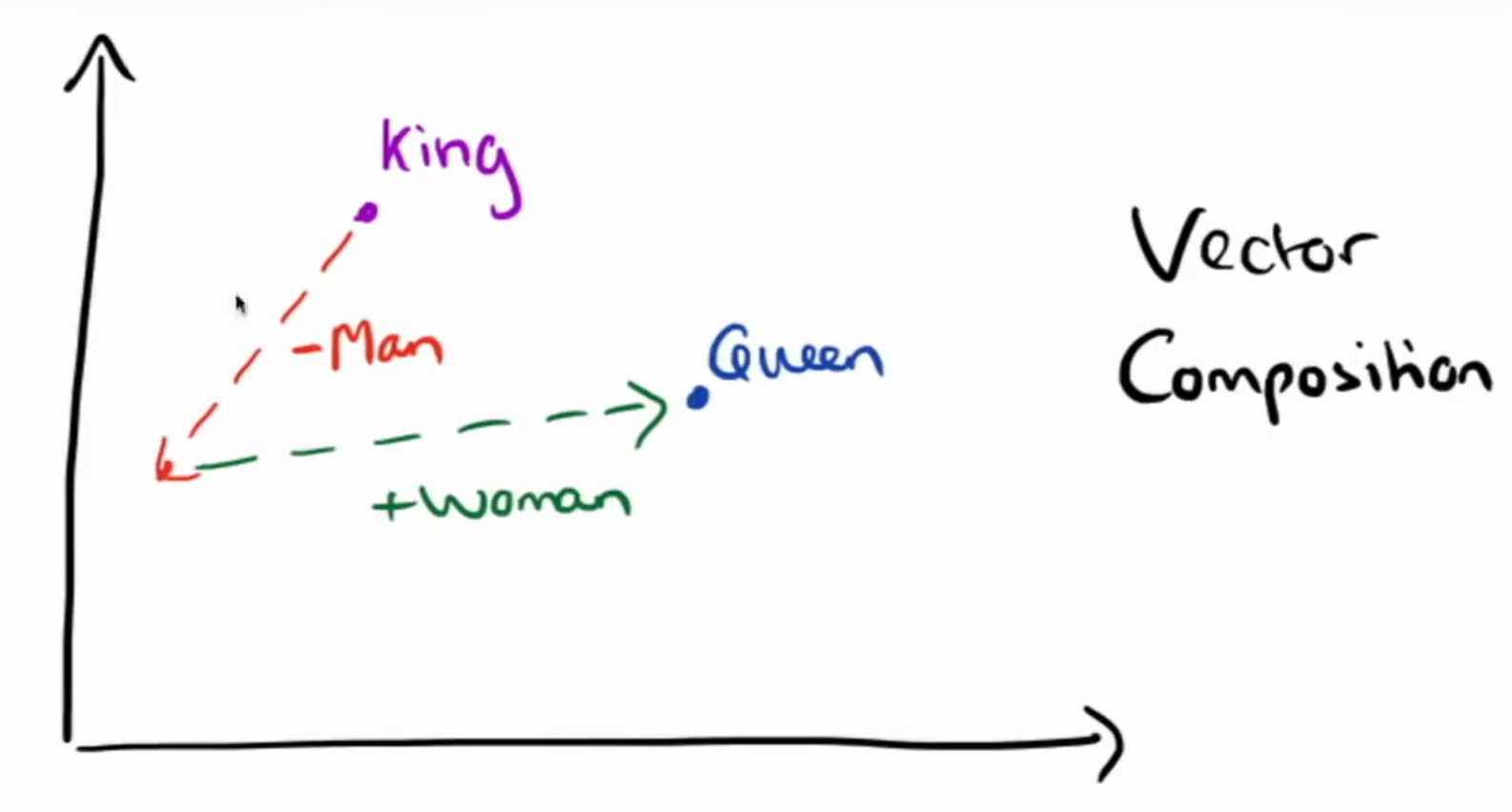
Looking at word vectors

• king - man + woman = queen 같은 수학을 지원할 수 있음