PTQ란?

1. PTQ의 기본 아이디어

• 이미 학습(Training)이 끝나서 높은 정확도를 달성한 모델(예: FP32 부동소수점)을 추가 학습 없이(또는 아주 최소한의 보정 과정만) 정수형(예: int8, int4)으로 변환하여 추론 속도나 메모리 사용량을 줄이는 것이 PTQ의 목표임.

• “추가 학습”이 없다는 것은, 오리지널 model의 parameter를 바꾸는 식의 Gradient Descent(Backprop) 같은 과정을 거치지 않는다는 뜻.

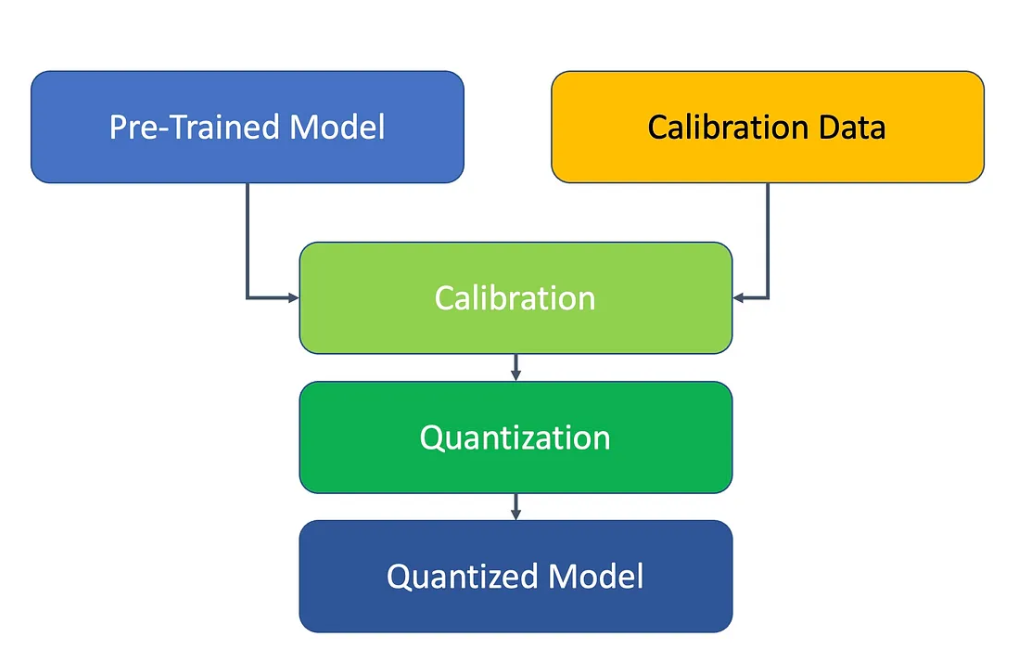
2. PTQ를 수행하기 위한 세팅

1. Pre-trained model(예: FP32)
   • 가령, 3개의 레이어(레이어1, 레이어2, 레이어3)를 갖고 있고, 현재 정확도가 99% 정도 되는 모델.
2. 소량의 캘리브레이션(calibration) 데이터
   • 모델의 통계(예: 활성화의 분포, 최대/최소값 등)를 추정하기 위해 필요한 적은 양(수백~수천 개 정도)의 입력 샘플.

• 이 데이터를 통해 가중치와 활성화의 스케일(scale)과 제로포인트(또는 min/max)를 추정하여 양자화 파라미터를 정한다.

3. PTQ의 단계별 과정 예시

단계 0. 모델 구조 파악

• 모델은 3개의 레이어로 구성: 레이어1 → 레이어2 → 레이어3.

• 이미 FP32로 학습되어 99% 정확도를 달성하고 있음.

단계 1. (옵션) Weight Quantization 먼저 진행

1. 가중치(Weights) 통계 수집
   레이어1, 2, 3 각각의 FP32 가중치 텐서(예: Conv나 FC의 파라미터)에 대해, $min, max$를 조사하거나, 좀 더 발전된 방식으로는 퍼센타일 클리핑(Percentile Clipping), KL Divergence 등을 활용하여 적절한 클리핑 범위를 구함.

2. 양자화 파라미터(Scale, Zero-Point) 계산

• 예: int4로 양자화한다고 하면, 표현 가능한 정수 범위가
  $[-8,7]$ (부호 있는 4비트) 정도가 될 텐데,
  실제 가중치 분포 $[w_{min}, w_{max}]$를 이 범위에 맞게 매핑하기 위한 스케일(scale)과 제로포인트(zero-point)를 계산.

3. 가중치 라운딩(Rounding)

• 각 레이어의 FP32 가중치를, 위에서 구한 스케일과 제로포인트를 사용해 정수(int4) 값으로 변환.

• $\hat{w} = \text{clip}\left(\text{round}\left(\frac{w}{\text{scale}} + \text{zero\_point}\right), -8, 7\right)$

• 이렇게 하면 가중치는 이미 정수 4비트 형태로 변환됨.

• 아직까지 활성화(Activation)는 FP32 상태로 둔 채, 가중치만 정수로 바뀐 상태에서 모델을 구동해볼 수 있음.

단계 2. Activation Quantization을 위한 캘리브레이션

1. 소량의 캘리브레이션 데이터 준비

• 예: 1000장 정도의 이미지(혹은 태스크에 맞는 입력).

2. FP32 입력 → (int4 가중치) 모델 추론

• 이제 레이어1에 입력이 들어가고, 레이어1의 정수 가중치와 곱해져서 중간 출력(활성화, 아직은 FP32)이 나옴.

• 레이어2, 레이어3도 마찬가지로 정수 가중치를 사용하여 중간 출력을 생성함.

3. 각 레이어별 활성화(Intermediate Tensor) 통계 수집

• 레이어1 출력, 레이어2 출력, 레이어3 출력 각각에 대해 최소/최대값 (혹은 히스토그램, 퍼센타일 등) 추적.

• 이것이 활성화의 분포를 파악하는 과정임.

4. 활성화 양자화 파라미터(Scale, Zero-Point) 계산

• 예: 레이어1의 활성화 범위가 $[-2.5, 3.1]$ 정도 나왔다면, 이를 int8 (예: $[-128, 127]$) 범위에 매핑할 수 있도록 scale과 zero-point를 구함.

• 레이어2, 레이어3도 마찬가지로 해당 활성화 분포에 맞춰 scale/zero-point 계산.

단계 3. Activation Quantization (Optional - Offline vs. On-the-fly)

• 최종 추론 때는, 활성화도 int4/ int8 등으로 변환해서 연산하는 식을 구현해야 함.
  1. On-the-fly Quantization
  추론 시, 레이어1의 출력을 FP32 → int4/8로 바로 변환(라운딩+클리핑)
  다음 레이어에 정수곱(int4/8 × int4/8)을 수행
  2. Offline Quantization (드문 케이스)
  캘리브레이션 데이터의 활성화를 미리 정수로 변환해놓고 확인하는 방식.

결론

"PTQ는, 사전 학습된 모델을 별도의 재학습 없이 정수로 변환하기 위해, 소량의 캘리브레이션 데이터로 가중치/활성화의 분포를 분석하여 (스케일, 클리핑 범위 등) 최적 파라미터를 구하고, 이 값에 맞춰 반올림해 정확도 손실을 최소화하는 과정이다."

ps

“PTQ로 양자화된 모델의 추론은, 대개 (1) 입력을 정수화 → (2) 정수 가중치와 정수 연산 → (3) 결과 활성화도 정수로 다시 클리핑 → (4) 다음 레이어로 전달 … 식으로 진행하며, 필요 시 처음/마지막 단계에서만 FP로 변환한다.”