1. 릴레이션 스키마의 설계
논리적 데이터베이스의 설계하는 과정으로 관계 모델을 이용해서 실세계를 표현한다.
1-1. 스키마 설계 고려사항
i) 애트리뷰트, 엔티티, 관계성을 파악한다
ii) 관련된 애트리뷰트들을 릴레이션으로 묶는다
- 애트리뷰트간의 관계성을 데이터 종속성이라고 한다.
ex) 학생(학번, 이름) 릴레이션이 있다면, 학번이 정해지면 이름이 정해지는 종속관계를 가진다.
iii) 변칙적 성질을 예방한다
- 삽입, 삭제, 갱신 시 이상현상이 없도록 설계해야한다
1-2. 이상현상
- 삽입 이상 : 데이터 삽입 시 원치 않는 정보까지 강제적으로 삽입해야하는 이상현상
- 삭제 이상 : 데이터 삭제 시 연쇄 삭제로 인해 의도치 않은 정보까지 손실하는 이상현상
- 갱신 이상 : 하나의 데이터를 갱신할 때 여러 데이터를 한번에 갱신해야해 일관성일 깨질 수 있는 이상현상
이런 이상현상들은 여러 종속 관계를 하나의 릴레이션으로 표현해서 발생한다. 종속을 분해해서 각각의 릴레이션으로 표현해서 해결할 수 있다. 즉 하나의 종속성을 하나의 릴레이션으로 표현하는 것이고, 이를 정규화라 한다.
1-3. 스키마 설계와 변환
스키마 설계는 데이터베이스의 논리적 설계로 가장 먼저 실행하여 내부와 외부 스키마 설계의 바탕이 된다. 스키마 변환은 종속성에 따라 릴레이션을 분할하는 것으로 정규화와 같은 말이다.
2. 함수 종속 (Functional Dependency)
R(X, Y)에서 X가 정해지면 Y가 정해지는 관계를 함수 종속 관계라하고 X -> Y로 표현한다.
X -> Y 함수 종속 관계에서 X를 결정자(determinant), Y를 종속자(dependent)라 한다. 이때 X와 Y는 각각 두 개 이상의 애트리뷰트일 수 있다.
2-1. 키와 함수 종속
R(X, Y)에서 X가 기본 키면 R의 모든 애트리뷰트 Y에 대해 X -> Y이 성립한다. 따라서 X -> R(t)가 성립한다. 최종적으로 하나의 X를 찾고 모든 이외의 애트리뷰트는 X로 결정되게 하는 것이 목표이지만, 이는 우리의 목표이지 X->Y 관계에서 X가 키를 뜻하는 것은 아니기 때문에 X의 한 값에 대응하는 Y가 다수 존재할 수 있다.
2-2. 함수 종속 다이어그램
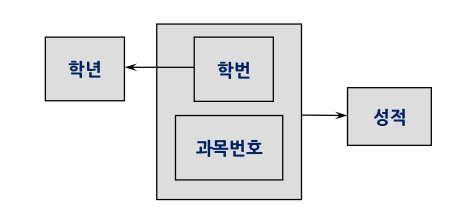
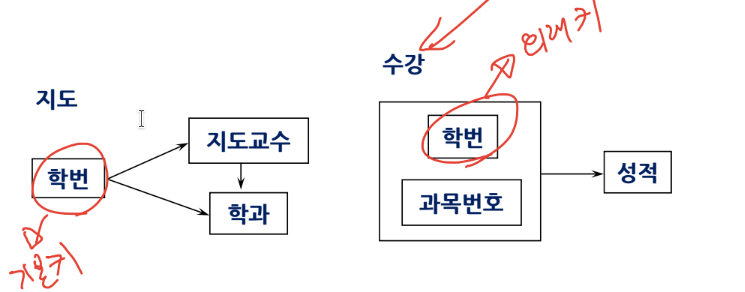
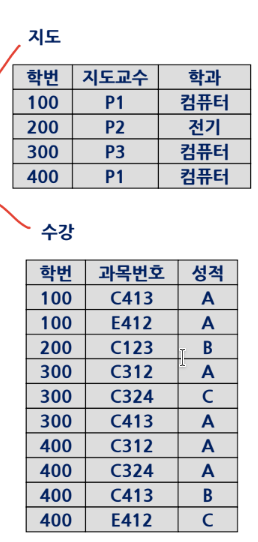
수강(학번, 과목번호, 학년, 성적) 릴레이션을 다음과 같이 다이어그램으로 표현할 수 있다.
2-3. 완전 함수 종속과 부분 함수 종속
X가 2개 이상의 애트리뷰트를 가지고 X -> Y 일 때
- 완전 함수 종속 : X' ⊂ X, X' -> Y 인 X'가 없을 때
- 부분 함수 종속 : X' ⊂ X, X' -> Y 인 X'가 있을 때
2-2. 다이어그램에서 학년은 {학번, 과목번호}과 부분 함수 종속 관계가 있고, 성적은 완전 함수 종속 관계가 있다.
2-4. 함수 종속 추론 규칙 (inference rules)
- 반사 (reflexive) : A ⊇ B 이면 A -> B
- 첨가 (augmentation) : A -> B 이면 AC -> BC, AC -> B
- 이행 (transitive) : A -> B, B -> C 이면 A -> C
- 분해 (decomposition) : A -> BC 이면 A -> B, A -> C
- 결합 (union) : A -> B, A -> C 이면 A -> BC
함수 종속은 데이터의 의미적 제약조건을 나타낸다. DBMS는 함수 종속을 유지하기 위해 스키마에 명세하고, 보장할 방법을 제공해야한다. 2-2 그림을 예로 들자면 만약 (학번, 과목번호) -> (성적) 함수 종속이 유지되지 않으면 한 학생이 하나의 과목에 대해 여러개 성적을 가지는 등 의미적으로 잘못된 데이터가 존재할 수 있다.
2-5. 함수 종속의 closure
-
릴레이션의 데이터 중복 방지를 위해 모든 함수 종속을 찾는 것이 이상적이다
-
함수 종속 집합 F와 추론될 수 있는 모든 함수 종속의 집합을 함수 종속 F에 대한 closure이라 하고
F+로 표현한다.
R(A, B, C, G, H, I)
F = {A->B, A->C, CG->H, CG->I, B->H}
F+ = {A->B, A->C, CG->H, CG->I, B->H, A->H, CG->HI, AG->H, AG->I}함수 종속은 스키마를 설계하기에 앞서 필요한 데이터들 그리고 그들의 관계를 파악하기 위해 필요하다. 당연히 closure를 찾기 어렵고, 해당 도메인에 대한 전문가와 데이터베이스 전문가가 면담을 통해 분석하고 발견해야 올바른 데이터베이스 요구사항을 설정하고 스키마를 설계할 수 있다.
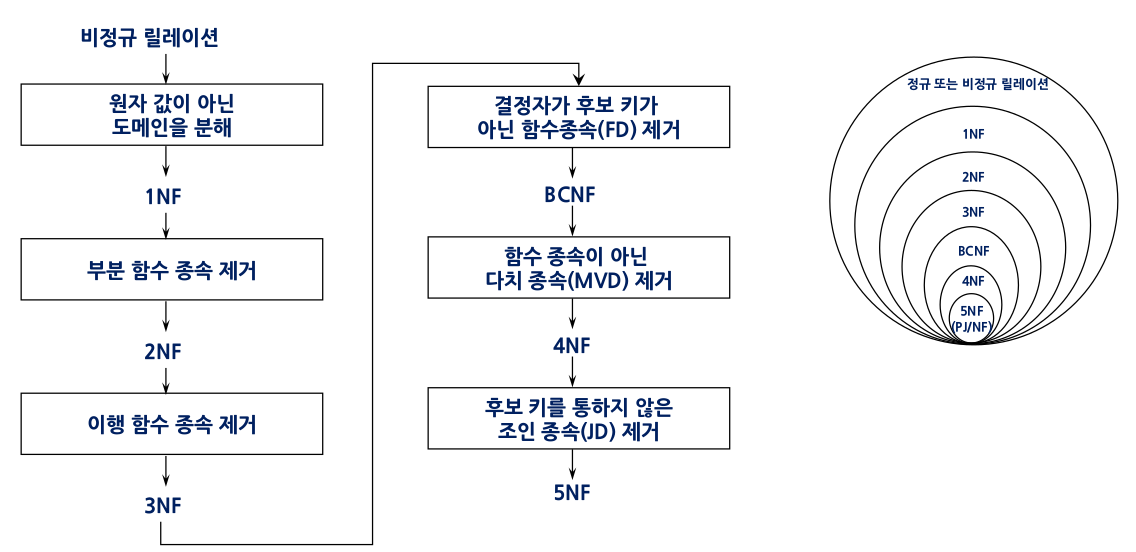
3. 정규형
일련의 제약조건을 만족하는 릴레이션을 정규형이라하고 스키마 변환(정규화)을 통해 만든다.
정규화의 원칙
i) 정보 표현의 무손실
- 분할한 릴레이션을 조인하면 원래의 릴레이션과 같은 정보를 표현해야한다.
- 무손실 분해 : 원래 릴레이션에서 얻을 수 있는 정보는 분해된 릴레이션을 조인해 얻을 수 있다. 역은 성립 X
ii) 최소의 데이터 중복
iii) 분리의 원칙
- 독립된 관계성은 별도의 릴레이션으로 분리하여 표현해야한다.
3-1. 제1정규형 (1NF)
모든 도메인이 원자값으로 된 릴레이션
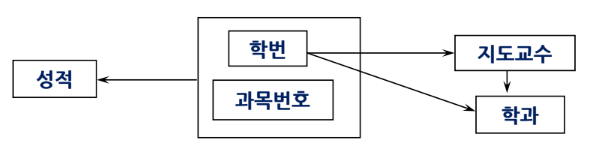
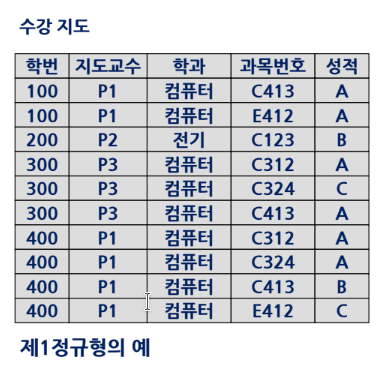
이상현상 원인 : 기본 키에 부분 함수 종속
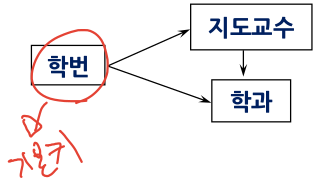
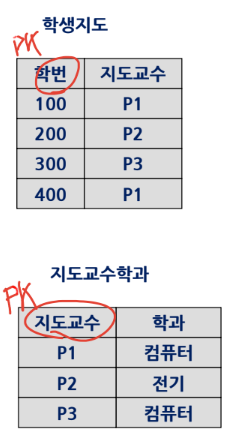
3-2. 제2정규형 (2NF)
1NF이고, 키가 아닌 애트리뷰트는 모두 키에 대해 완전 함수 종속인 릴레이션
즉 기본 키에 대해 부분 함수 종속 관계를 기준으로 무손실 분해한 것이다.
- Heath의 무손실 분해 정리 : R(A, B, C), A -> B이면 R1(A, B), R2(A, C)로 무손실 분해 할 수 있다.
이상현상 원인 : 이행적 함수 종속
- 이행적 함수 종속 : A->C, A->B, B->C 일때 C는 A에 이행적 함수 종속이다.
3-3. 제3정규형 (3NF)
2NF이고, 기본 키가 아닌 애트리뷰트들은 기본 키에 이행적 함수 종속 되지않은 릴레이션
즉, 기본 키에 대해 이행적 함수 종속이 없다.

특징
- 키가 아닌 애트리뷰트 갱신 시 이상현상이 발생하지 않는다
- 모든 이원 릴레이션은 3NF이다
- 다음의 경우 3NF 이지만 이상 현상이 발생할 수 있다.
i) 복수의 후보키를 가지며
ii) 모든 후보키가 두 개 이상의 애트리뷰트로 구성되고
iii) 후보키들의 애트리뷰트가 서로 중첩되는 경우
- 이상현상이 발생하는 3NF 릴레이션 예)
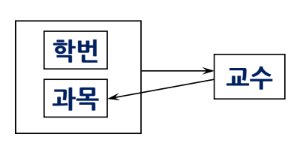
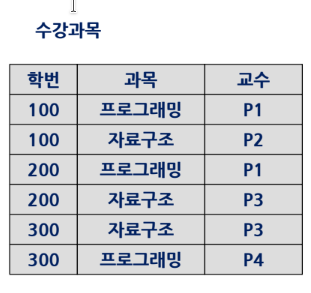
이상현상 원인 : 후보 키가 아닌 결정자
3-4. 보이스/코드 정규형 (BCNF)
3NF이고, 결정자가 모두 후보 키인 릴레이션. 강한 3NF라고도 한다.
즉, 후보 키가 아닌 결정자가 있다면 분할한 정규형이다.
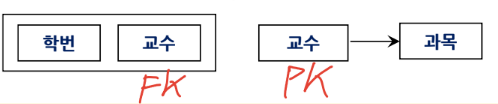
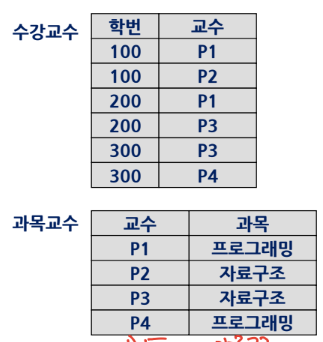
이상현상 원인 : 함수 종속이 아닌 다치 종속
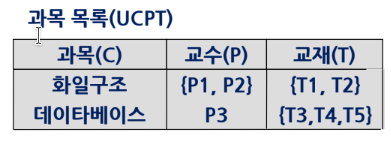
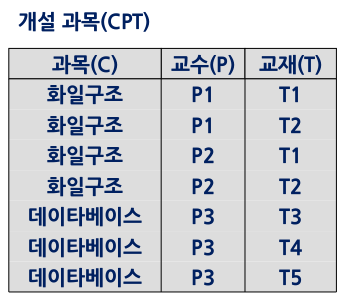
A, B, C가 릴레이션 R의 애트리뷰트의 부분 집합이라 할 때, 애트리뷰트 쌍 (A, C)-값에 대응되는 B-값의 집합이 A-값에만 종속되고 C-값에는 독립적이면 B는 A에 다치 종속이라 하고 A ↠ B로 표기한다. 이때 A ↠ C도 성립하여 A ↠ B|C가 성립한다.
3-5. 제4정규형 (4NF)
BCNF이고, 모든 다치 종속이 함수 종속인 릴레이션
즉, 함수 종속이 아닌 다치 종속이 없거나 A ↠ B|C를 A ↠ B, A ↠ C로 분해한 릴레이션
- 일반적으로 4NF까지 분해하면 스키마를 잘 설계할 것이라 할 수 있다.
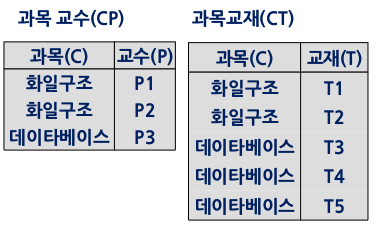
3-6. 제5정규형 (5NF)
모든 조인 종속(JD)이 후보 키를 통해 성립되는 릴레이션
즉, 조인 종속(JD)에 포함되는 애트리뷰트 부분 집합은 모두 기본 키이다
- 조인 종속으로 인한 문제는 겪기 어려울 뿐더러 모든 JD를 찾아내느 것은 어렵기 때문에 JD를 만족하면 반드시 분해햐야한다는 것은 아님
4. 정리