1. 부동소수점
-
고정소수점을 이용하면 수를 표현할 수 있는 범위가 고정된다
-
과학적 표기법으로 부동소수점을 이용할 수 있다
ex) 1.01 * 2^10
2. 부동소수점 표준
- 32bit single precision과 64bit double precision
S = sign bit, 0(양수) 1(음수)

1.0 <= 정규화 significand <= 2.0
-
1.은 항상 연산되기 때문에 fraction 비트로 표현하지 않아도 된다
fraction은 과학적 표기법에서 1.을 제외한 숫자이다 -
exponent는 항상 unsigned되도록 하기위해 Bias를 추가해서 비트에 표현한다
single bias = 127, double bias = 1023
3. 부동소수점의 표현 범위
Exponent 값 00000000과 11111111은 0과 무한을 표현하기 위해 비워둔다
3-1. 표현 가능한 가장 작은 값
32bit
- Exponent = 00000001, 실제 지수 = 1 - 127 = -126
- Fraction = 000...00, 실제 가수부(significand) = 1.0
- 최소값 = ±1.0 2^-126, 약 ±1.2 10^-38
64bit
- 최소값 = ±1.0 * 2^-1022
3-2. 표현 가능한 가장 큰 값
32bit
- Exponent = 11111110, 실제 지수 = 254-127 = 127
- Fraction = 111..11, 실제 가수부 = 2.0
- 최대값 = ±2.0 2^127, 약 3.4 10^38
64bit
- 최대값 = ±2.0 * 2^1023
3-3. 부동소수점 정확도
- 32bit : 2진수 23자리, 10진수 약 6자리
- 64bit : 2진수 52자리, 10진수 약 16자리
4. 부동소수점 예시
-0.75를 표현하라
= -1 * 1.1 * 2^-1
S = 1
32bit Exponent = -1 + 127 = 126 = 01111110
64bit Exponent = -1 + 1023 = 1022 = 01111111110
Fraction = 1000...00
Single : 1011111101000...00
Double : 1011111111101000...00
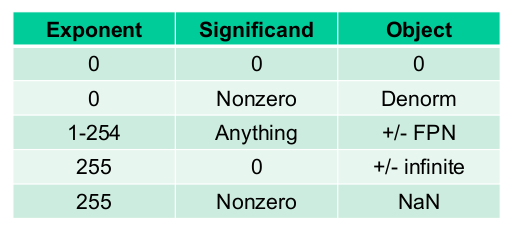
5. 무한과 Not-a-Number
5-1. 무한
- Exponent = 111...11, Fraction = 000...00 이면 ±∞
- 부동소수점에서 0으로 나누면 오버플로우가 발생하지않고 ±∞를 나타내야한다
- 따라서 X/0 > Y는 가능한 비교이다
5-2. NaN
- Exponent = 111...11, Fraction ≠ 000...00 이면 NaN
- 실수가 아니라는 뜻이다. 따라서 0.0/0.0 이나 sqrt(-4.0)은 NaN이다
- NaN와 연산시 결과는 NaN이다
6. 비정규값
- 부동소수점에서 0 주변에 표현할 수 있는 값 간에 차이가 커진다
0에서 최소값 차이 = 2^-126
최소값에서 2번째 값 차이 = 2^-149
- 원인 : 부동소수점의 정규화에 따른 1.의 포함
6-1. 해결
- 해결 : Exponent = 00...0, Fraction ≠ 00...0
비정규 값 : 1.을 포함하지 않고 지수를 -126으로 고정한다
- 표현가능한 비정규 최소값 = 0.000...01 * 2^-126 = 2^-149
- 표현가능한 비정규 2번째 값 = 0.000...10 * 2^-126 = 2^-148

- 비정규값을 이용하면 수가 작을 때 계산이 precision을 점점 잃게해 gradual underflow라고도 한다
7. 부동소수점 덧셈
1) 자리수를 맞춘다
2) significands를 더한다
3) 정규화하고 over/underflow를 확인한다
4) 필요시 반올림하고 다시 정규화한다

