1. 우선순위 큐의 구현
우선순위에 따라 요소 순서를 결정하는 FIFO가 아닌 큐
구현 방법 : 우선순위를 키로 정의해서 큐를 만든다
- 클래스 계층 구조
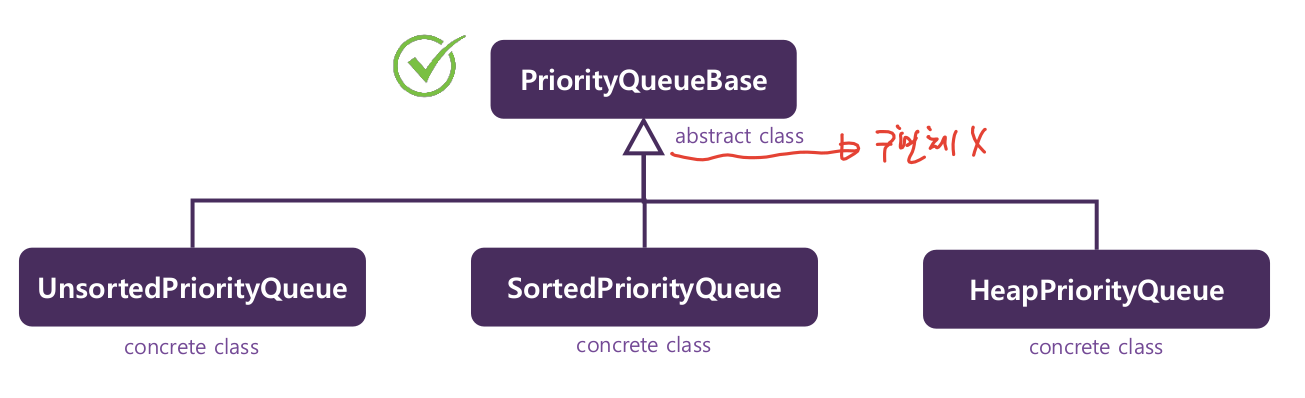
- 사용 예
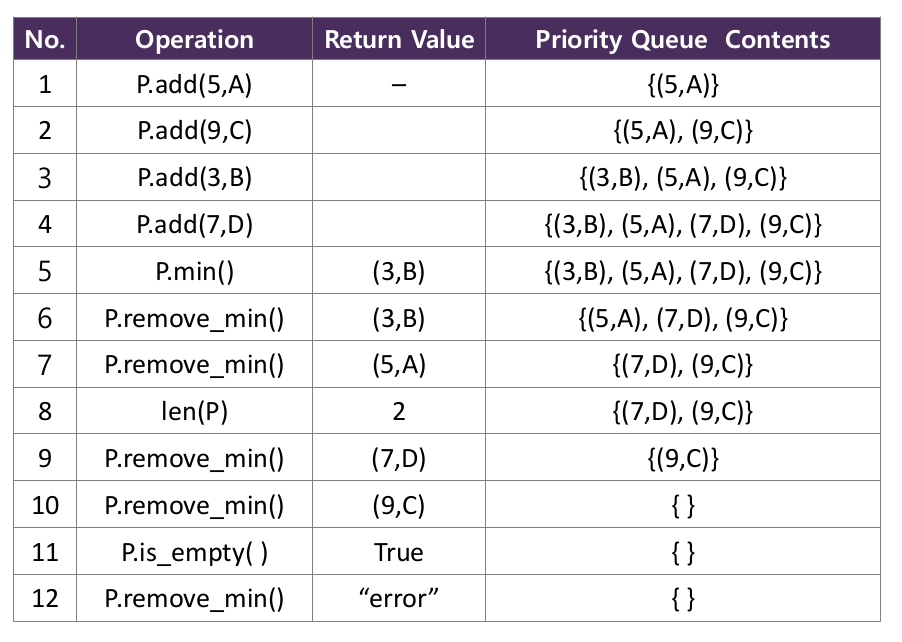
1-1. 정렬되지 않은 리스트로 구현
-
UnsortedPriorityQueue
i) Enqueue : 리스트 끝에 새로운 (키, 값) 추가
ii) Dequeue : 매번 리스트에서 최소 키 아이템을 찾음 -
기본 연산 성능

1-2. 정렬된 리스트로 구현
-
SortedPrioritQueue
i) Enqueue : 리스트가 정렬되도록 (키, 값)을 추가할 위치 찾음
ii) Dequeue : 리스트의 첫 아이템 -
기본 연산 성능

1-3. 힙을 이용하여 구현
-
HeapPriorityQueue
i) Enqueue : 힙 성질을 유지하도록 (키, 값) 추가
ii) Dequeue : 힙 성질을 유지하도록 루드 노드를 꺼냄 -
기본 연산 성능

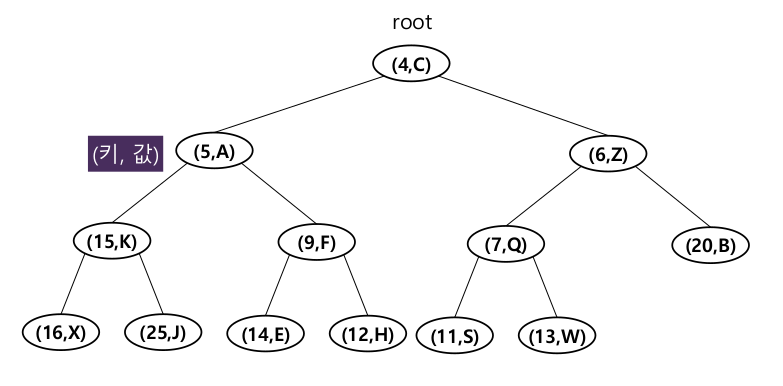
1-3-1. 힙
부모가 자식보다 작은 키 값을 갖는 완전 이진 트리
-
힙 순서 속성 : 루트를 제외한 모든 키는 부모의 키보다 크거나 같다
-
완전 이진 트리 속성 : 레벨 i에는 2^i 노드가 있고 레벨 h는 노드가 왼쪽에 몰려있다
-
힙의 높이 : n개의 요소를 저장하는 힙 T의 높이 h는 log n(내림) 이다
1-3-2. 힙의 추가/삭제 연산
- 추가 : 요소를 마지막 위치에 추가 후 업 힙 버블링을 수행한다
업 힙 버블링 : 부모 노드의 키가 나의 키보다 크면 재귀적으로 교환한다
예) (2,T)를 추가
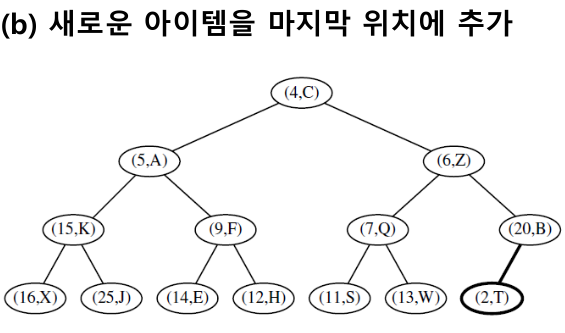


- 삭제 : 루트(최고 우선순위)를 삭제한 후 마지막 노드를 루트로 옮겨 다운 힙 버블링을 수행한다
다운 힙 버블링 : 자식 노드의 키가 나의 키보다 작으면 재귀적으로 교환한다. 단 자식 중 작은 키와 교환한다

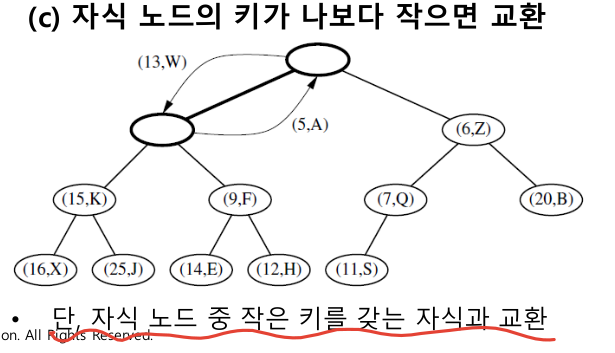
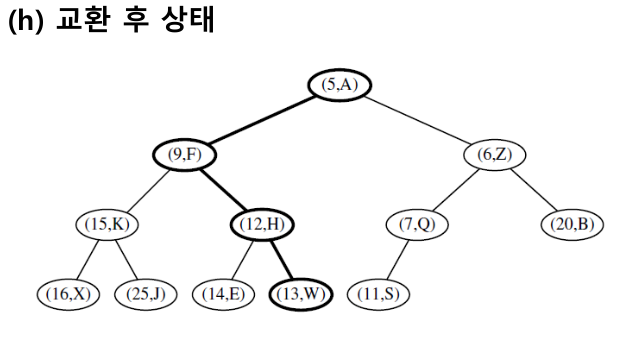
1-3-3. 힙의 배열 표현
힙을 배열로 구현하면 새로운 아이템을 마지막 노드에 추가할 때 편리하다

1-3-4. 하-상향식 힙 구성
O(n)에 힙을 구성할 수 있다.
힙을 구성할 때 n번 add()를 호출해서 구성한다면 시간복잡도 = O(nlogn). 힙을 아래서부터 위로 구성하는 하-상향식 힙 구성으로 O(n)에 힙을 구성할 수 있다. 여러개의 작은 힙을 요소를 추가하며 점점 합쳐 하나의 힙을 구성하는 방식으로 작동한다.
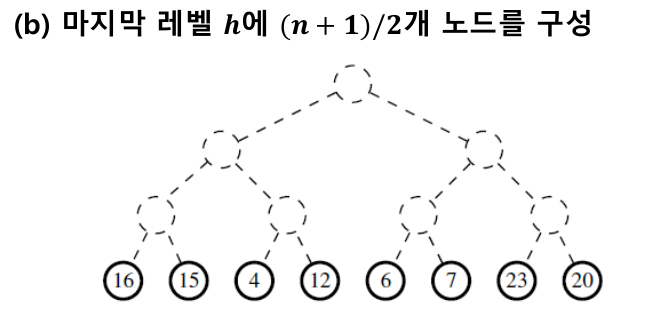
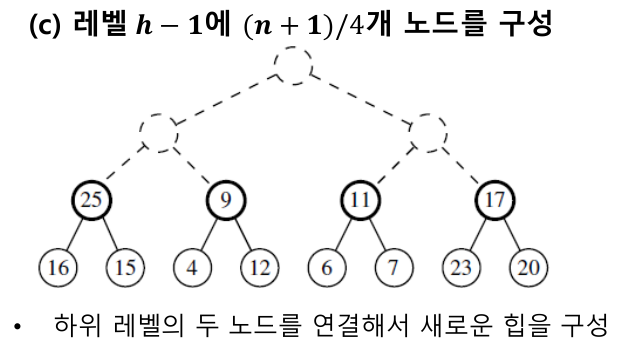
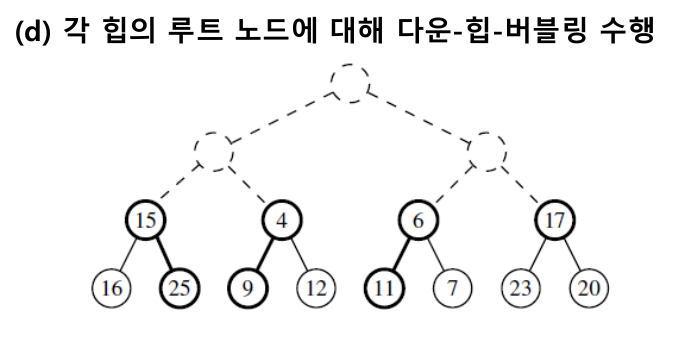 반복 후
반복 후

2. 우선순위 큐를 이용한 정렬
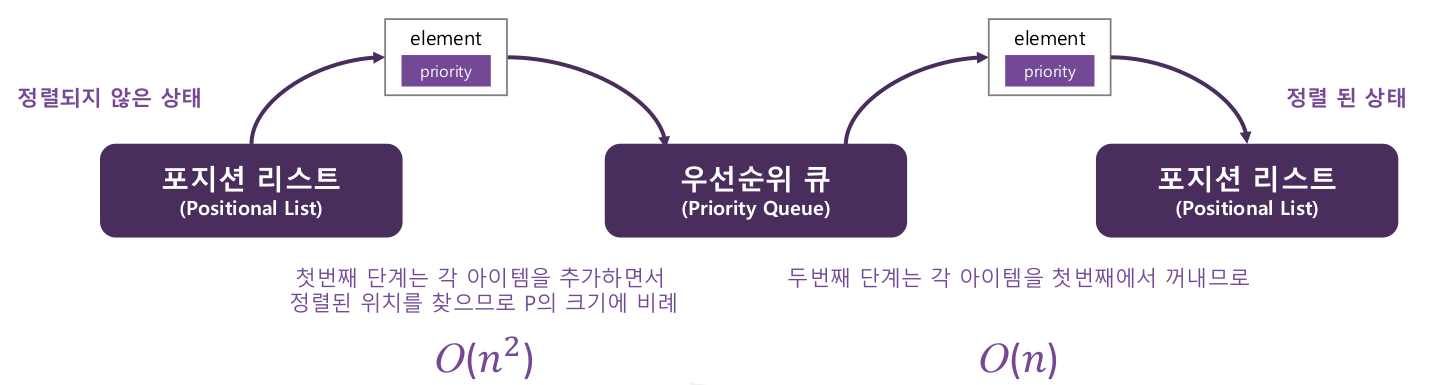
리스트에 우선순위 큐로 이동 후 다시 리스트로 이동해서 정렬할 수 있다.
2-1. 선택 정렬
- 정렬되지 않은 리스트로 구현된 우선순위 큐를 사용하면 선택 정렬이 된다
- 시간 복잡도는 선형구조 정렬의 한계치인 O(n^2)이다

2-2. 삽입 정렬
- 정렬된 리스트로 구현된 우선순위 큐를 사용하면 삽입 정렬이 된다
- 시간 복잡도는 선형구조 정렬의 한계치인 O(n^2)이다
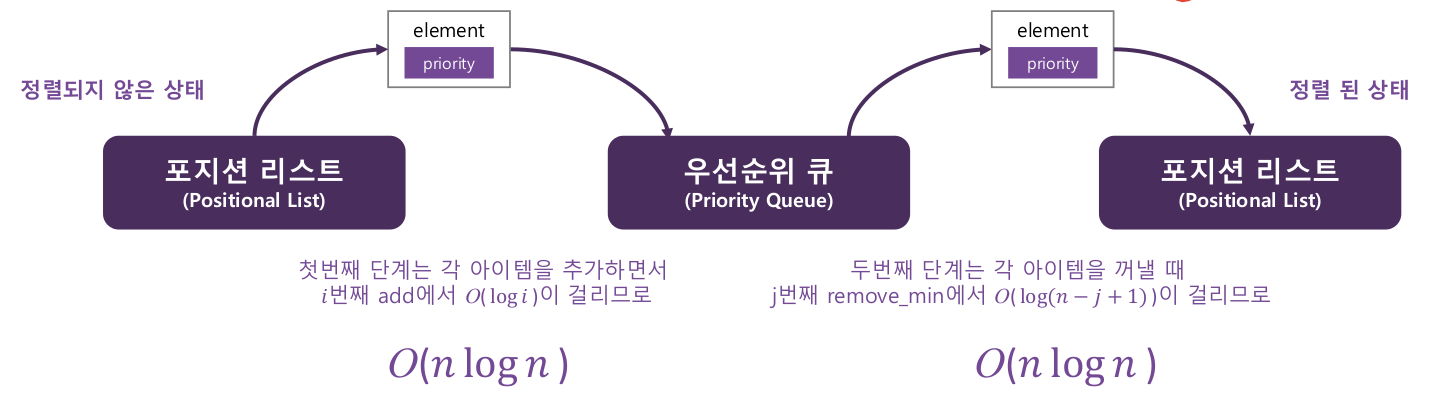
2-3. 힙 정렬
- 힙으로 구현된 우선순위 큐를 사용하면 힙 정렬이 된다
- 시간 복잡도는 가장 효율적인 정렬 복잡도인 O(nlogn)이다
2-4. 제자리에서 힙 정렬
- 배열 기반으로 힙 구현 시 하나의 배열에서 힙 정렬이 가능하다
- 우선순위 큐가 최대 키를 먼저 출력하도록 변경해야한다

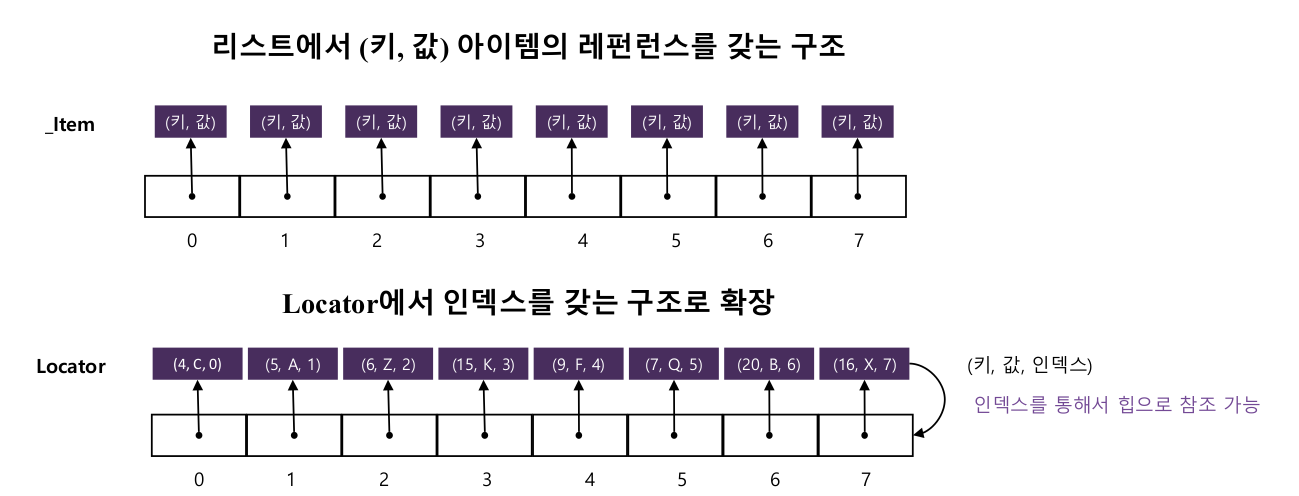
3. 조정가능한 우선순위 큐
임의의 아이템을 큐에서 제거하거나 우선순위가 변경되는 큐
(키, 값, 인덱스)를 관리하는 Locator 구조로 임의 아이템 제거와 우선순위 변경을 할 수 있다