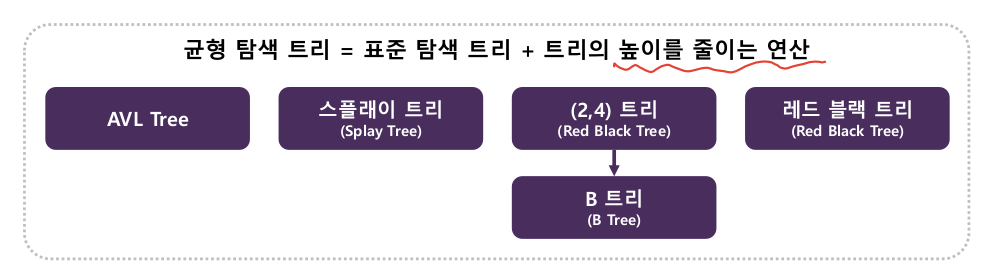
1. 탐색 트리
정렬 맵을 탐색 트리로 구현하면 O(log n) 시간복잡도를 갖는다

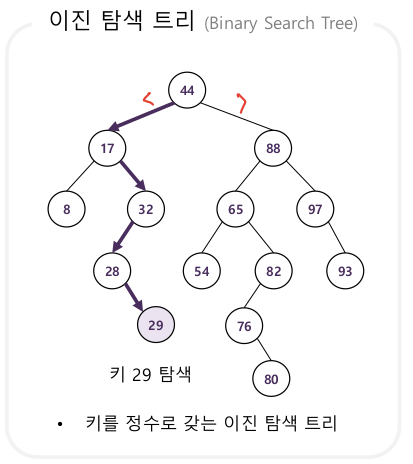
2. 이진 탐색 트리
이진 트리로 위치 p에 (키, 값)이 저장되어 있다 = 의사 결정 트리

- 성질 :
i. p의 왼쪽 부트리의 키는 k보다 작다
ii. p의 오른쪽 부트리의 키는 k보다 크다
2-1 순회
이진 탐색 트리를 중위 순회하면 오름차순으로 키가 정렬된 순서로 노드를 방문한다
O(n)에 전체 트리를 순회하며 특정 위치에서 순회할 수 있다
-
첫번째 노드 = 루트에서 왼쪽 자식을 따라 내려간 리프 노드
-
마지막 노드 = 루트에서 오른쪽 자식으로 따라 내려간 리프 노드
-
이전 노드
i. 왼쪽 자식이 있는 경우 왼쪽 부트리에서 오른쪽 자식을 따라 내려간 리프노드
ii. 왼쪽 자식이 없는 경우 부모를 따라 올라가다 내가 포함된 오른쪽 자식을 갖는 첫번째 조상 노드 -
다음 노드
i. 오른쪽 자식이 있는 경우 오른쪽 부트리의 루트에서 왼쪽 자식을 따라 내려간 리프노드
ii. 오른쪽 자식이 없는 경우 부모를 따라 올라가다 내가 포함된 왼쪽 자식을 갖는 첫번째 조상 노드 -
이진 탐색 트리의 연산 시간복잡도 = O(h), 범위 탐색의 시간복잡도 = O(s+h) 이때 s = 범위 아이템 수
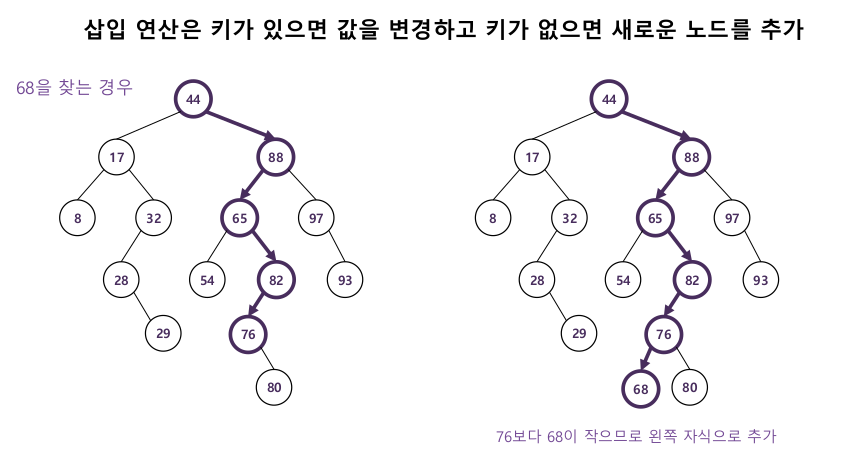
2-2. 삽입
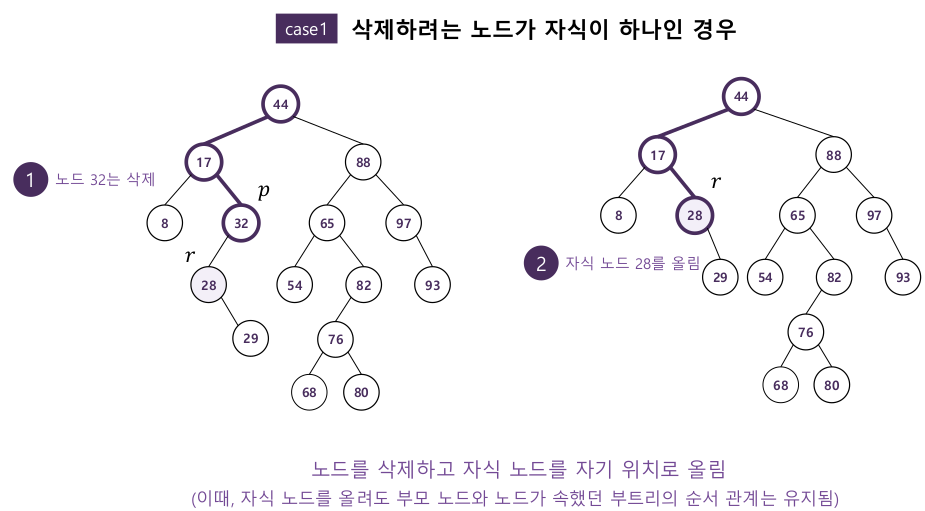
2-3. 삭제
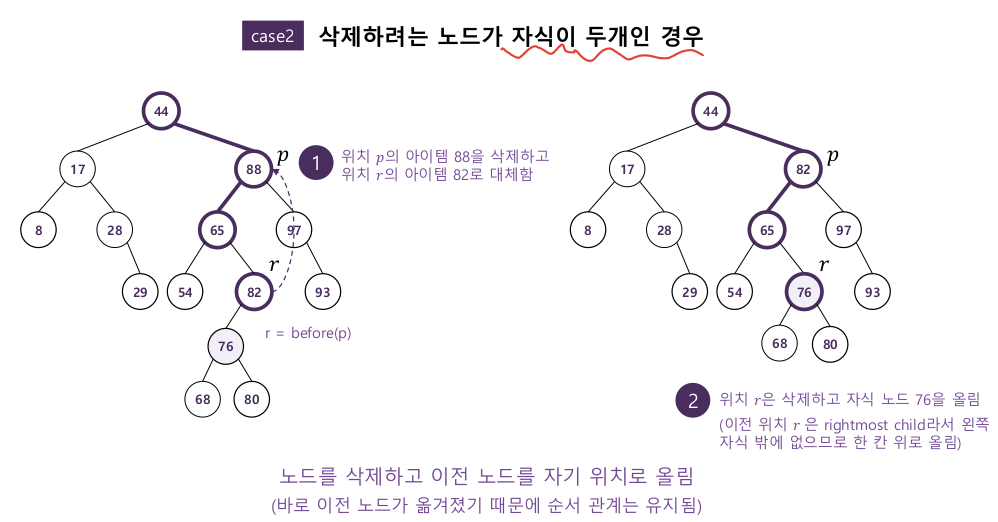
- 삭제하려는 노드의 자식 수에 따라 방식이 나뉜다
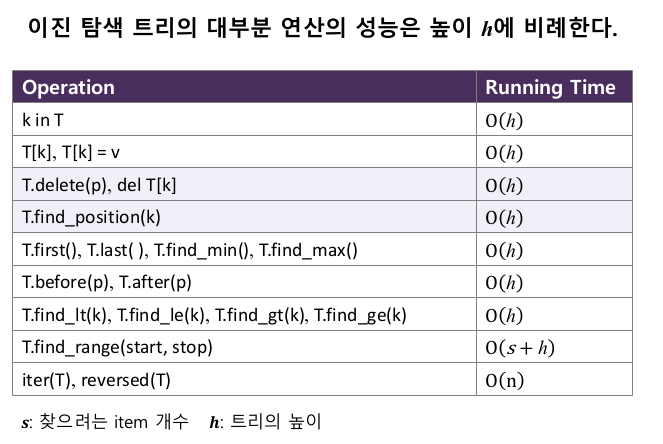
2-4. 이진 탐색 트리의 연산 별 성능
- O(h)이므로 평균 = O(log n), 최악 = O(n)
3. 균형 탐색 트리
이진 탐색 트리이고 최악의 경우 높이가 O(log n)인 트리
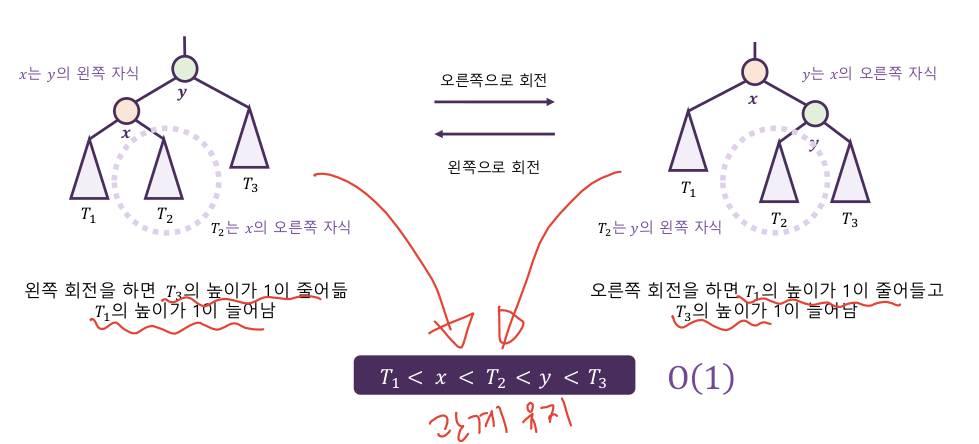
3-1. 주요 연산 : 회전
- 부모-자식 관계를 바꿔 순서 관계를 유지하며 트리 높이를 줄인다
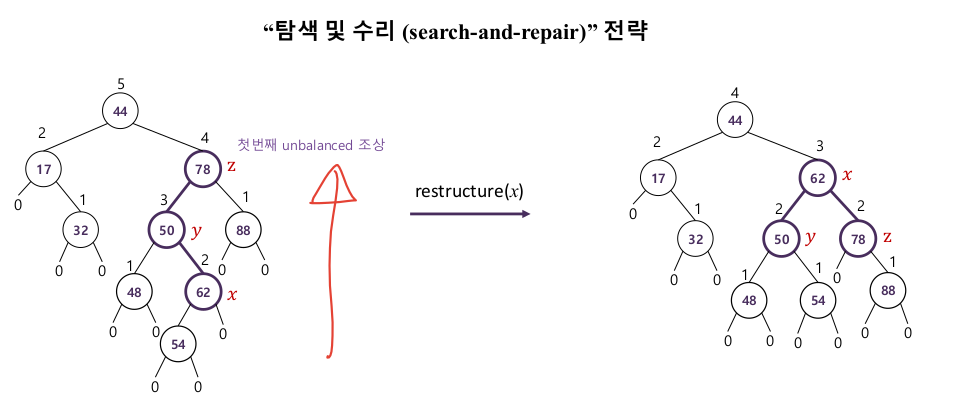
3-2. 주요 연산 : 재구조화
- 조부모와 손주의 경로를 줄여 트리 높이를 줄인다
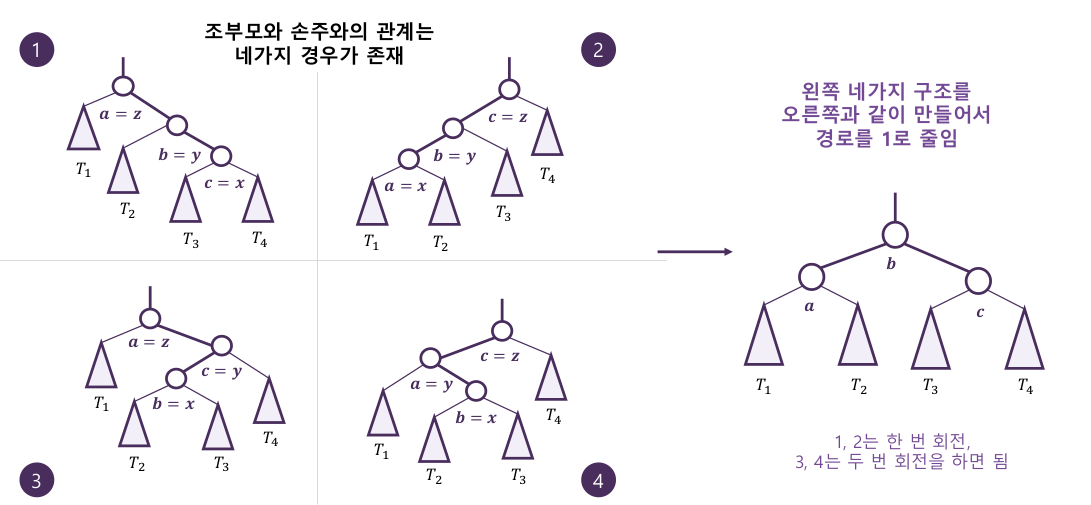
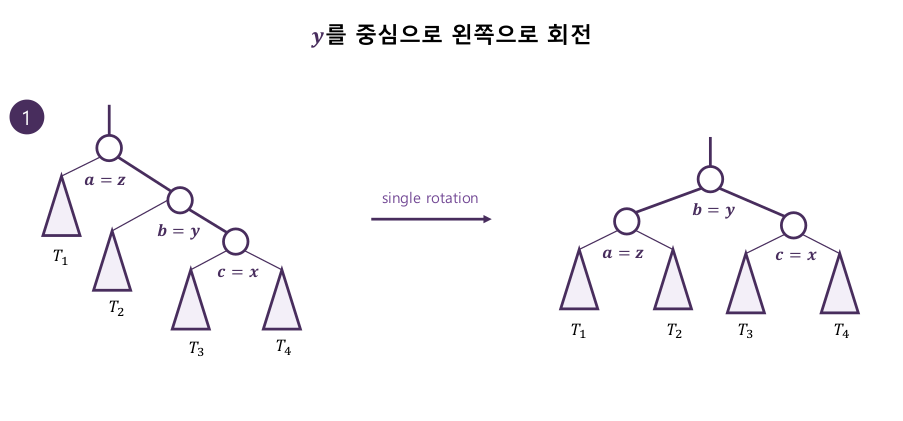
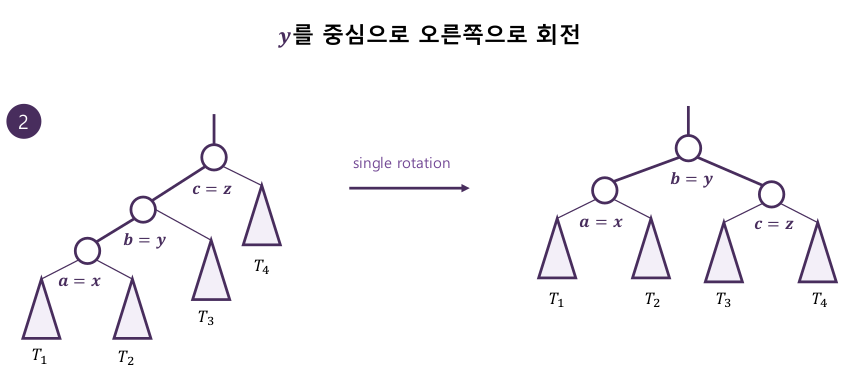

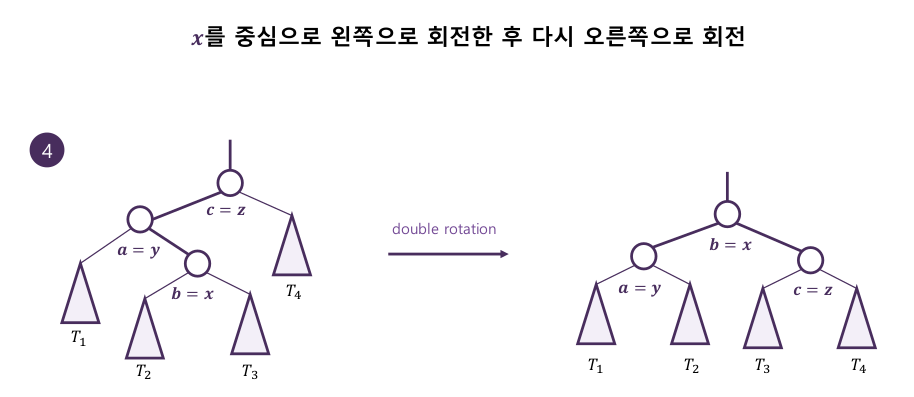
4. AVL 트리
높이-균형 속성을 만족하는 이진 탐색 트리
높이-균형 속성 : 각 노드에서 두 자식의 높이 차는 최대 1이다
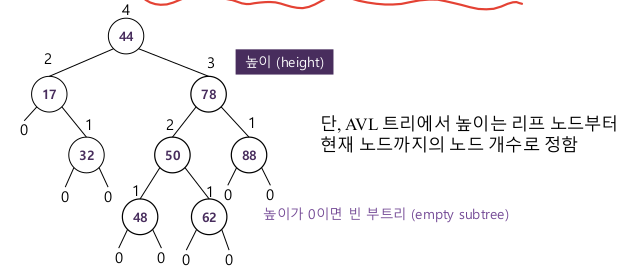
-
AVL 트리 높이 : 높이 계산 시 자신을 포함해서 노드 수를 센다
-
n개 아이템을 갖고 있는 AVL 트리의 높이 : O(log n)
4-1. AVL 트리 연산
- 이진 탐색 트리의 임의의 위치에서 자식 높이가 최대 1 차이나면 균형적, 아니면 불균형적

4-1-1. 삽입 연산
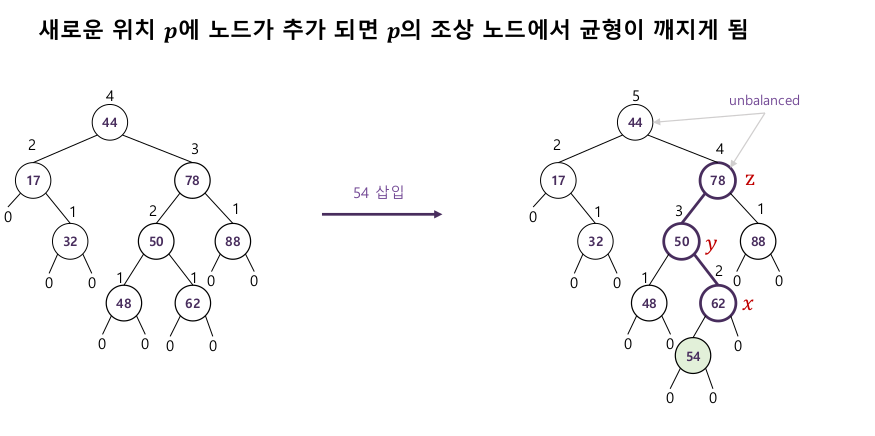
- 다음 조건의 x,y,z 노드를 찾으면 x노드를 재구조화 하여 트리 높이를 줄인다
i. 조부모(z) : p의 조상 중 첫번째로 만나는 불균형인 조상
ii. 부모(y) : z의 자식 중 높이가 더 높은 자식
iii. 자식(x) : y의 자식 중 높이가 더 높은 자식
4-1-2. 삭제 연산
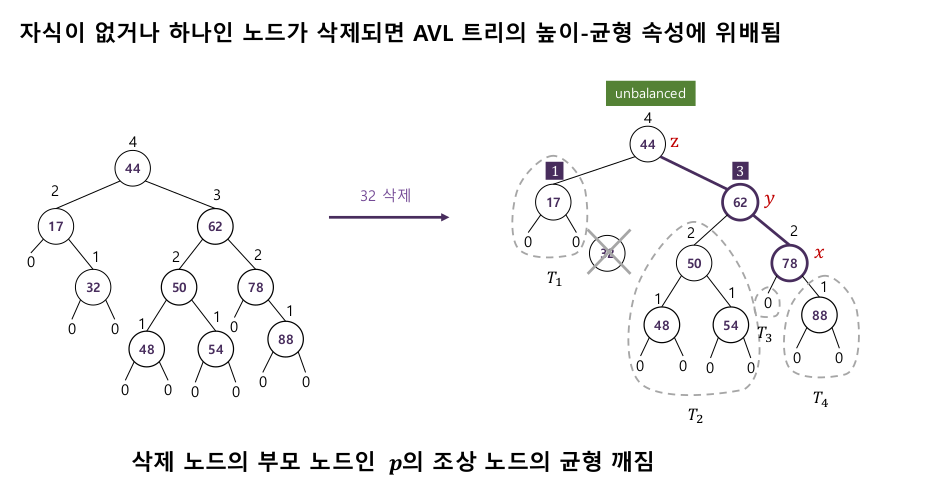
- 다음 조건의 x,y,z 노드를 찾으면 x노드를 재구조화 하여 트리 높이를 줄인다
i. 조부모(z) : p의 조상 중 첫번째로 만나는 불균형인 조상
ii. 부모(y) : z의 자식 중 높이가 더 높은 자식
iii. 자식(x) : y의 자식 중 높이가 더 높은 자식. 같을 경우 y와 같은 방향에 있는 자식 선호
4-2. 성능 분석
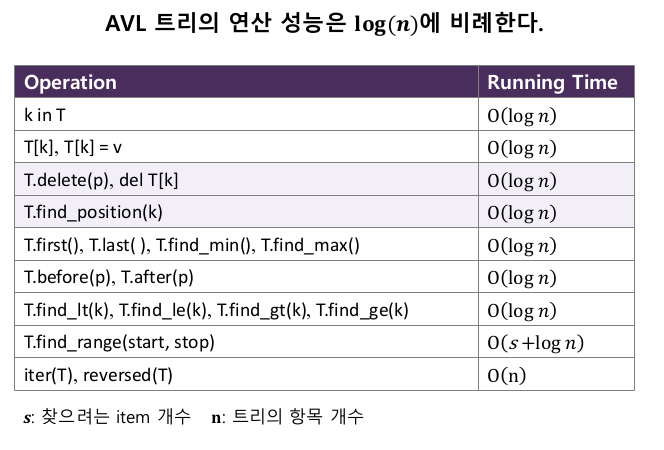
5. 스플레이 트리
빈번한 연산이 이뤄지는 노드를 루트로 옮겨서 트리 균형을 맞추는 이진 탐색 트리
5-1. 연산
5-1-1. Zig-Zig
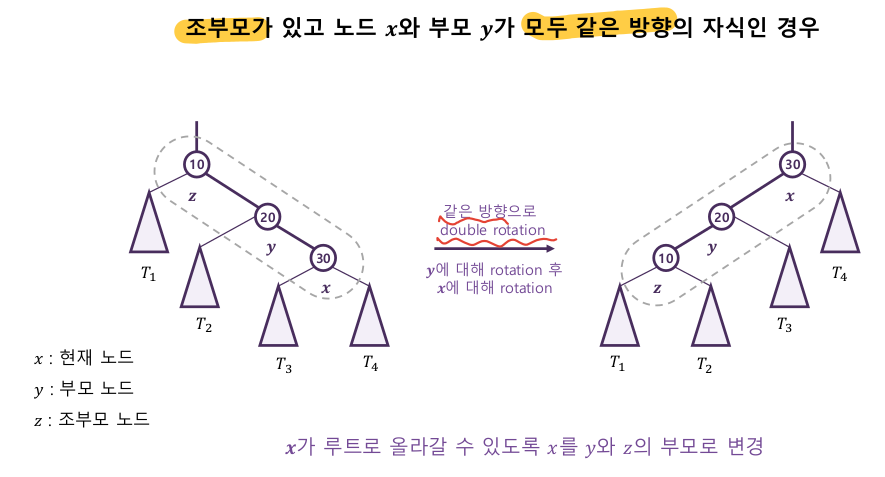
5-1-2. Zig-Zag

5-1-2. Zig
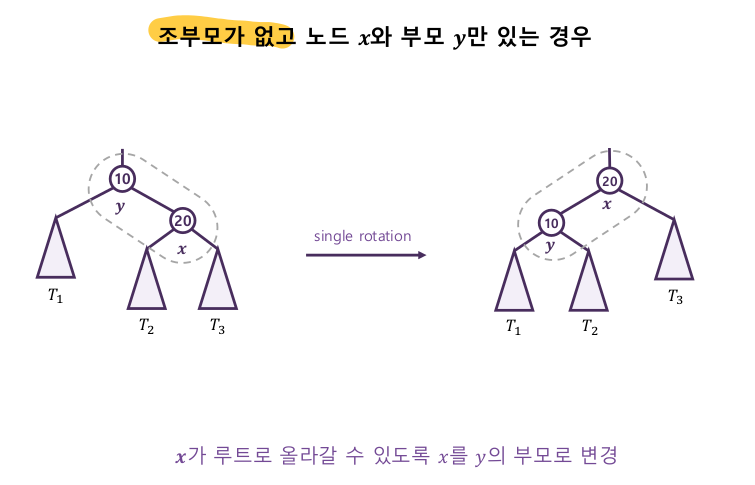
5-2. 탐색

5-3. 삽입
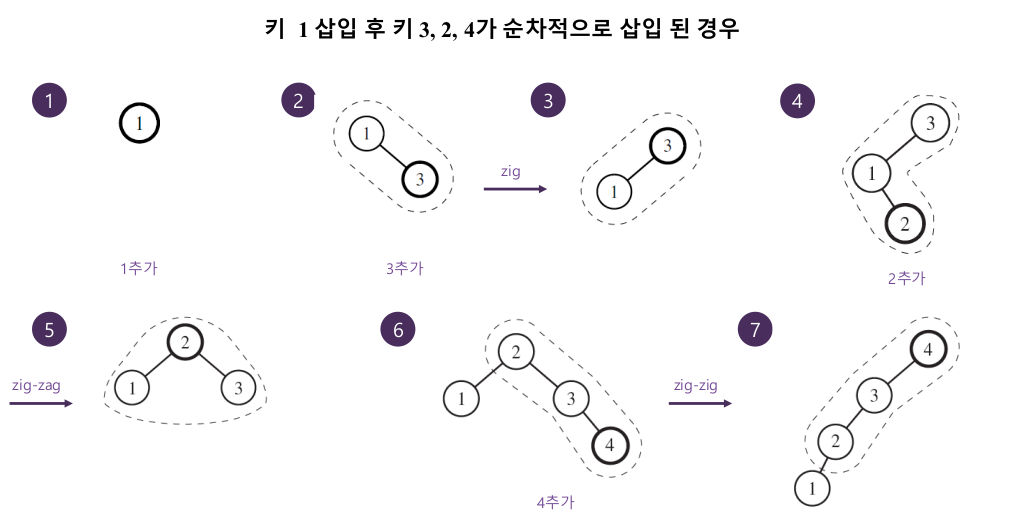
5-4. 삭제
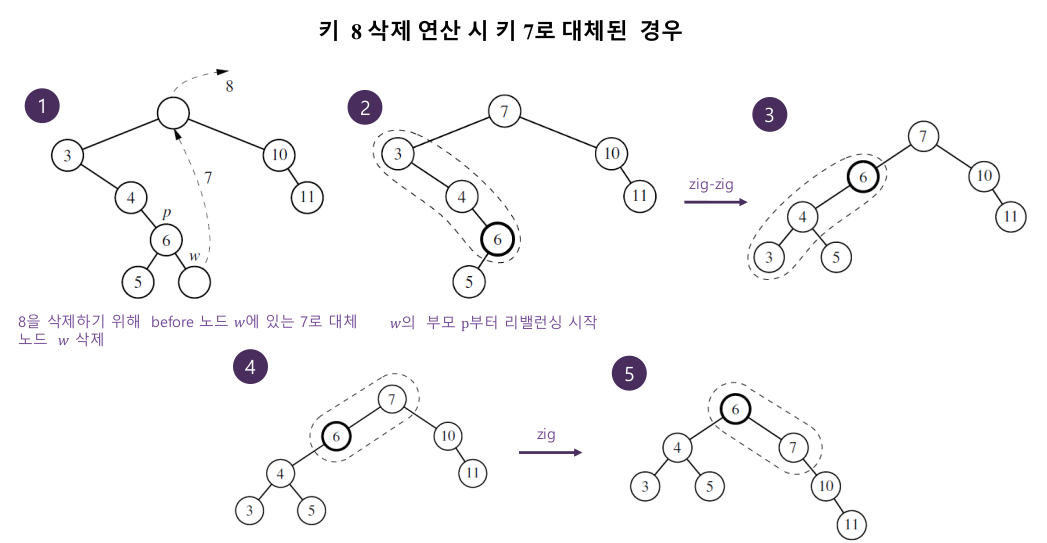
5-5. 성능 분석
-
탐색/삽입/삭제 연산 최악의 경우 O(h) 시간 소요, 분할 분석 시 O(log n) 시간 소요
-
위치 p의 깊이가 d라면, d/2(내림) 번 zig-zig or zig-zag 연산
d가 홀수면 가장 위에서 1번 zig 연산. 따라서 스플레이 연산은 O(d) 시간이 소요

6. (2-4) 트리
다중 탐색 트리 중 하나로 노드에 2-4개 키를 저장
6-1. 다중 탐색 트리
다중 탐색 트리 : 내부 노드에 자식이 2개 이상 있는 탐색 트리
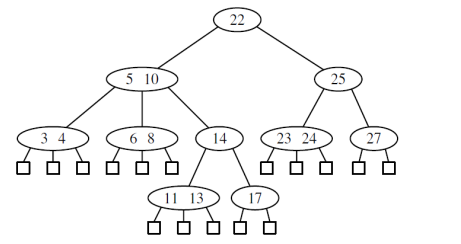
-
다중 탐색 트리가 순서 트리가 되려면 다음 성질을 만족해야한다
i. 내부 노드는 d-노드(자식이 d개인 순서 트리 노드)로 정의되며 d-1개 키를 저장
ii. 외부 노드는 데이터를 저장하지 않으며 정의 상 노드 역할만 하고 None으로 둠
iii. n개 아이템을 갖는 다중 탐색 트리는 n+1개의 외부 노드를 갖는다 -
시간복잡도 : O(log d), 이때 d = 노드의 자식 수
6-2. (2-4) 트리 연산
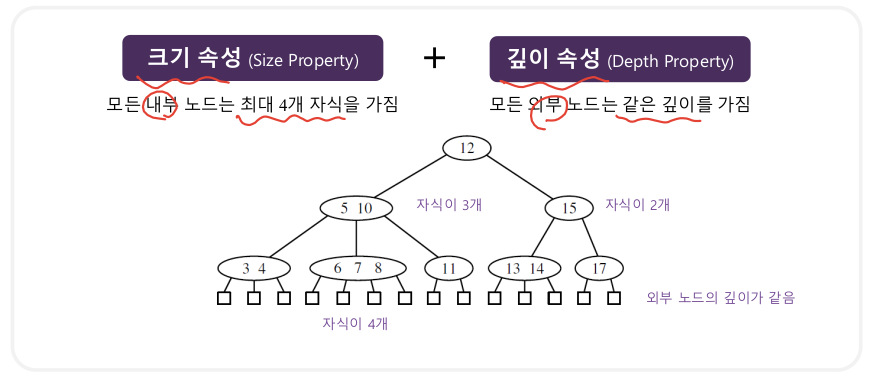
(2-4) 트리 = 다음 크기 속성과 깊이 속성을 만족하는 균형 다중 탐색 트리
-
높이 = O(log n)
-
탐색 시간 = O(log n)
-
노드에 사용할 맵 종류는 성능에 크게 영향을 못 미친다
6-2-1. 삽입
-
키 k를 탐색 했을 때 키가 없어서 외부 노드에서 탐색이 종료되었다면 외부 노드의 부모 노드에 키 삽입
-
오버플로 발생 시 노드를 분할해서 크기 속성을 만족하도록 한다
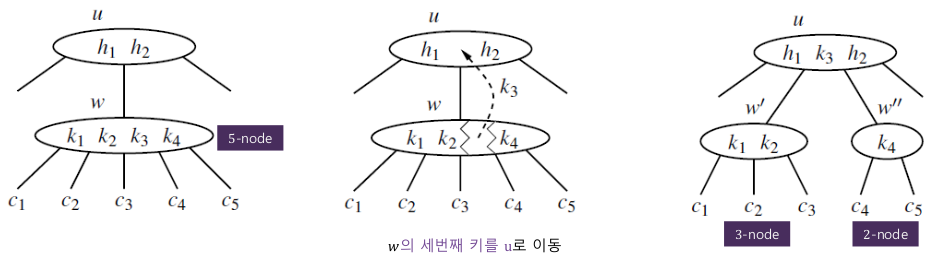
- 탐색 : O(log n), 각 분할 연산 : O(1) 이고 분할 횟수는 높이에 제한되므로 전체 분할 과정 : O(log n)
6-2-2. 삭제
- 항상 외부 노드를 자식으로 갖는 노드에서만 이뤄진다
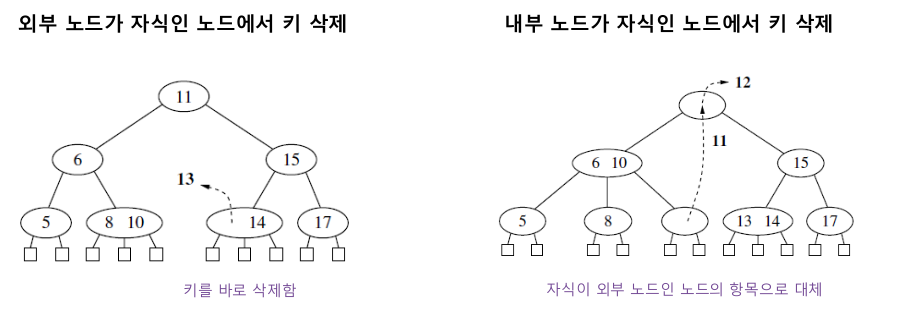
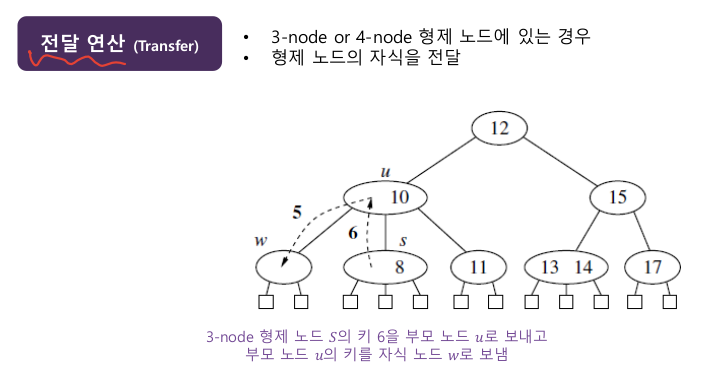
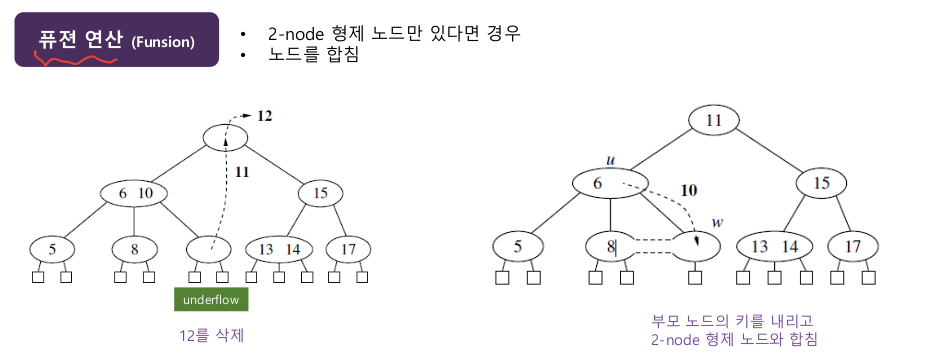
- 언더플로 발생 시 전달/퓨젼 연산을 통해 크기 속성을 만족하도록 한다
6-3. 성능 분석
- 대부분 연산이 O(log n)안에 이뤄진다
i. n개 항목 저장 시 높이 = O(log n)
ii. 각 분할, 전달, 퓨전 연산 = O(1)
iii. 탐색, 삽입, 삭제 연산 O(log n)노드 방문
>> 빠른 맵 탐색 연산과 업데이트 연산을 제공한다
7. 레드-블랙 트리
블랙 깊이를 기준을 만족하도록 균형을 맞추는 이진 탐색 트리. (2-4)트리와 통치이다
-
속성:
i. 루트 속성 : 루트는 블랙이다
ii. 레드 속성 : 레드 노드의 부모/자식은 블랙이다
iii. 깊이 속성 : 자식이 없거나 하나인 노드는 블랙 싶이가 모두 같다 -
블랙 깊이 : 자신을 포함한 조상의 블랙 노드 수
-
트리 높이 : O(log n)
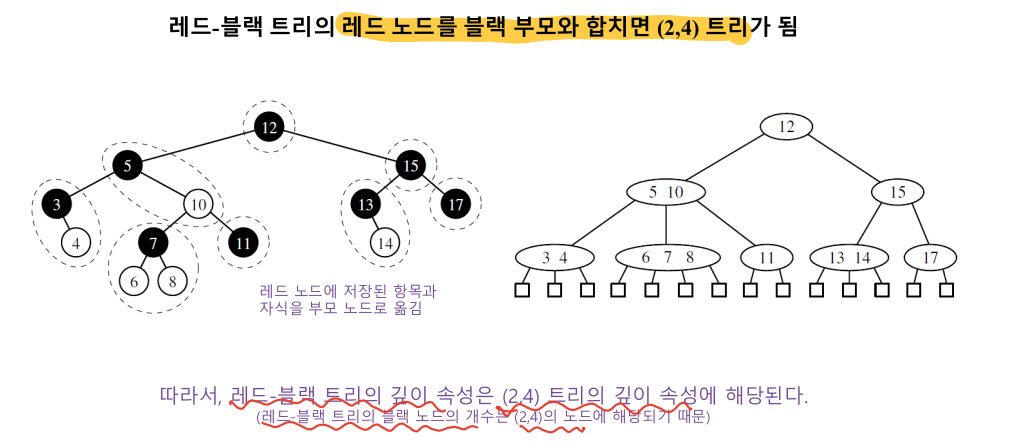
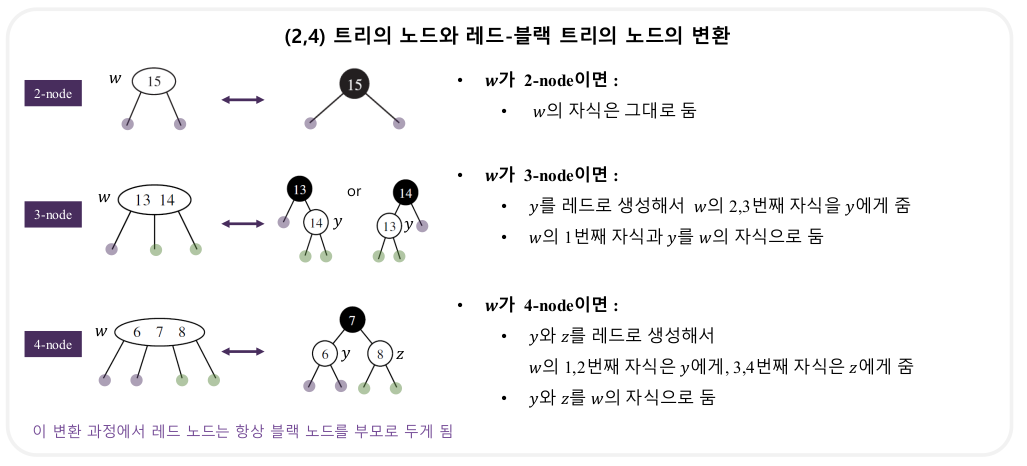
7-1. (2-4) 트리와 관계
- 상호 변환이 가능하다
7-2. 연산
7-2-1. 삽입
-
키 탐색을 했을 때 빈 부트리에 도달하면 리프 노드로 삽입한다 이때
a. 노드가 하나면 루트 노드이므로 블랙 노드로 삽입
b. 그 외는 레드 노드로 삽입 -
삽입으로 높이 속성은 만족하지만 레드 속성이 위배될 수 있다.
ie) 더블 레드


- 리컬러링 횟수는 트리 높이 절반 이상이 될 수 없으므로 O(log n)
7-2-2. 삭제
- 노드 삭제는 자식 수가 0 또는 1인 노드에서만 발생하고 3가지 경우로 구분

-
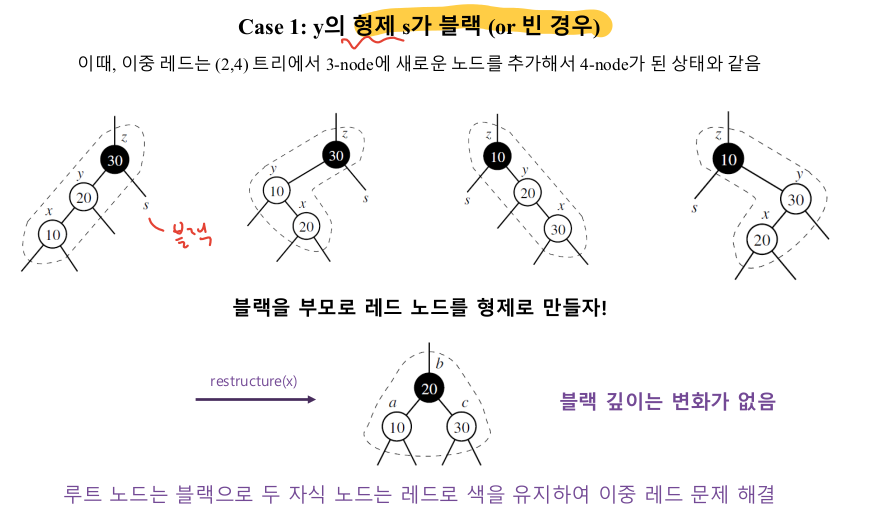
Case 1

-
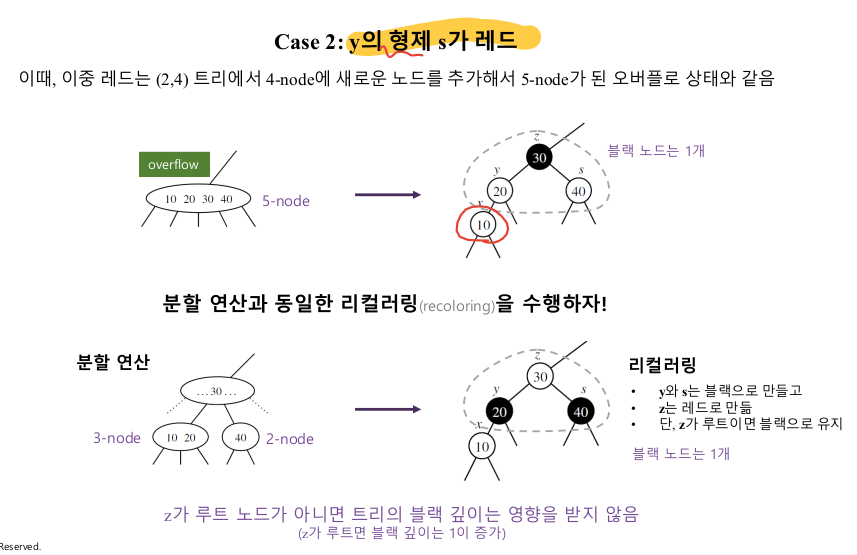
Case 2

-
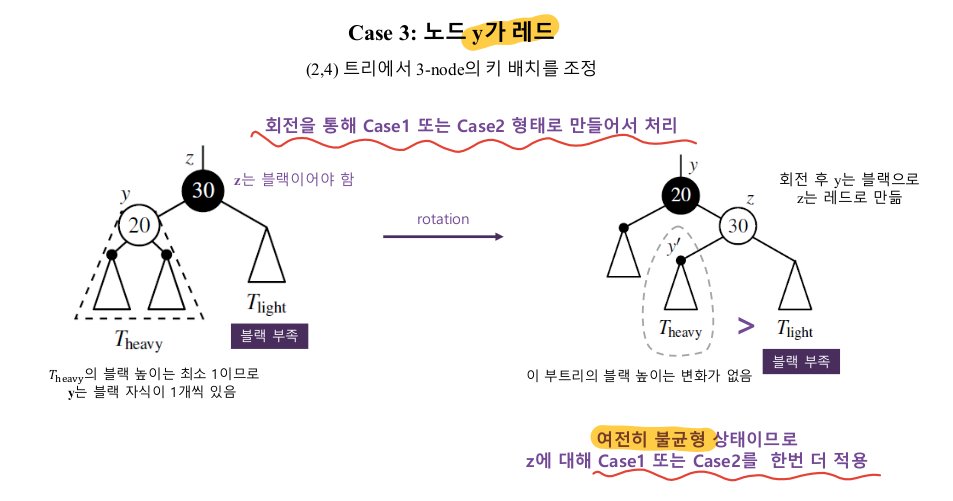
Case 3

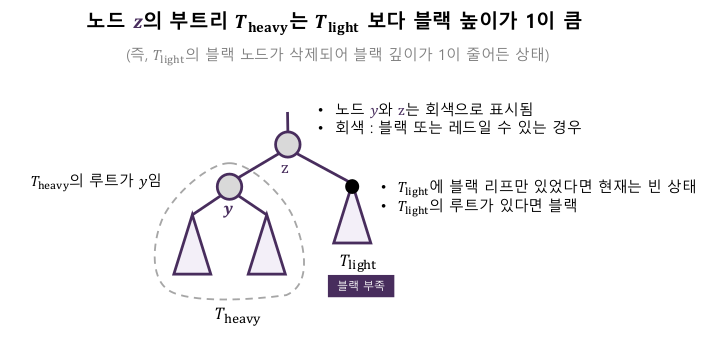
- 블랙 리프 삭제로 블랙 부족이 발생하면 3가지 경우로 처리한다



7-3. 성능 분석
-
대부분의 연산 O(log n) 보장
-
최대 장점 : 재구조화 연산 = O(1)
반면 AVL 트리, (2-4) 트리는 O(log n)의 구조 변경 필요 -
추가/삭제 연산 시
i. 탐색과 리컬러링 연산 : O(log n)
ii. 회전과 재구조화 연산 :O(1)