앞서 매우 큰 규모의 union-find 문제를 해결하는 효율적인 알고리즘 구현들을 살펴봤다. 이제 어떻게 그 알고리즘이 적용될 지를 보자.
엄청난 수의 union-find 응용들이 있다. 앞서는 네트워크에서의 동적 연결성에 대해 언급했었는데, 컴퓨터 인프라엔 다른 예가 많이 있다. 중요한 예로, 맨 아래를 보면 이미지 처리 분야에서 이미지 내의 영역(연결 컴포넌트에 대응)에 레이블(label)을 지정하는 방법을 들 수 있다.
나중에 우린 그래프 처리 알고리즘의 일종인 Kruskal의 최소 신장 트리(minimum spanning tree) 알고리즘을 살펴볼텐데, 이 알고리즘은 union-find를 서브루틴으로 사용한다.
물리학에서 물리 현상을 이해하기 위해서, 곧 이야기할 예시와 목록 상의 다른 것들을 포함해 알고리즘들이 많이 존재한다. 그래서, 이제 살펴보려는 것은 퍼콜레이션(percolation; 침투)이다.
Percolation
퍼콜레이션은 많은 물리계(phyiscal systems)에 적용 가능한 모델로, 퍼콜레이션의 추상 모델을 설명한 뒤 퍼콜레이션이 물리계에 어떻게 적용되는지 간단히 알아보자.
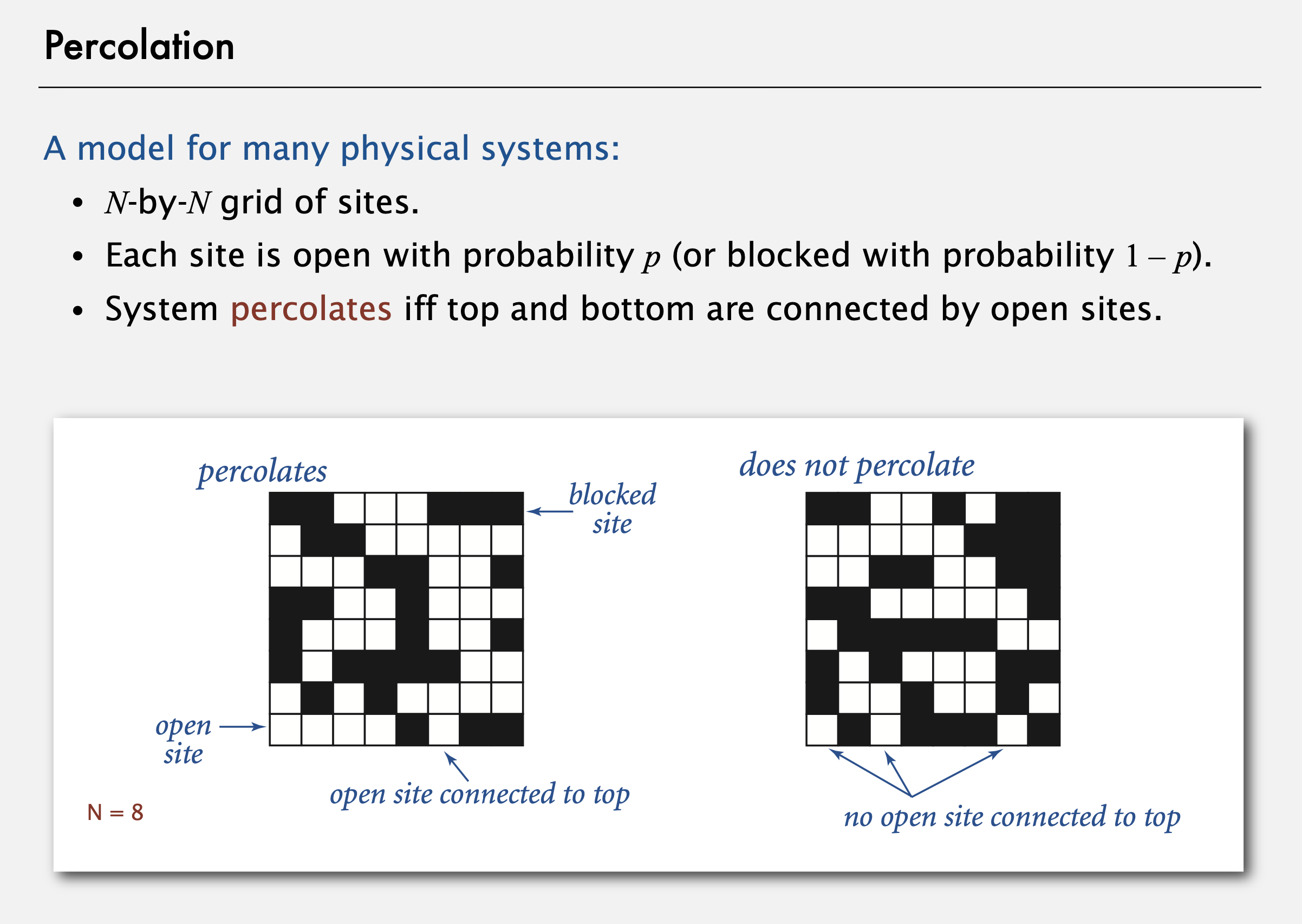
장소(site)라고 부르는 정사각형으로 이루어진 N*N 격자(grid)를 생각해 보자. 각 장소는 시작할 때 열림(open) 상태이다. 다이어그램엥서 각 장소는 확률 p로 열림(흰 색으로 표시)이고, 확률 1-p로 막힘(blocked; 검은 색으로 표시)이 된다. 격자로 나타내진 한 물리계는, 격자 상단과 하단이 열린 장소로 즉 연결되면 <- 침투되었다(percolated)고 불린다. 따라서 좌측의 계는 격자 상단에서 하단으로 흰 사각형을 따라 길을 찾을 수 있으므로 침투되었지만, 반면 우측의 계는, 격자 상단에서 하단으로 흰 사각형을 따라 갈 길이 없으므로 침투되지 않았다.
이 모델은 많은 물리계를 나타낼 수 있다.
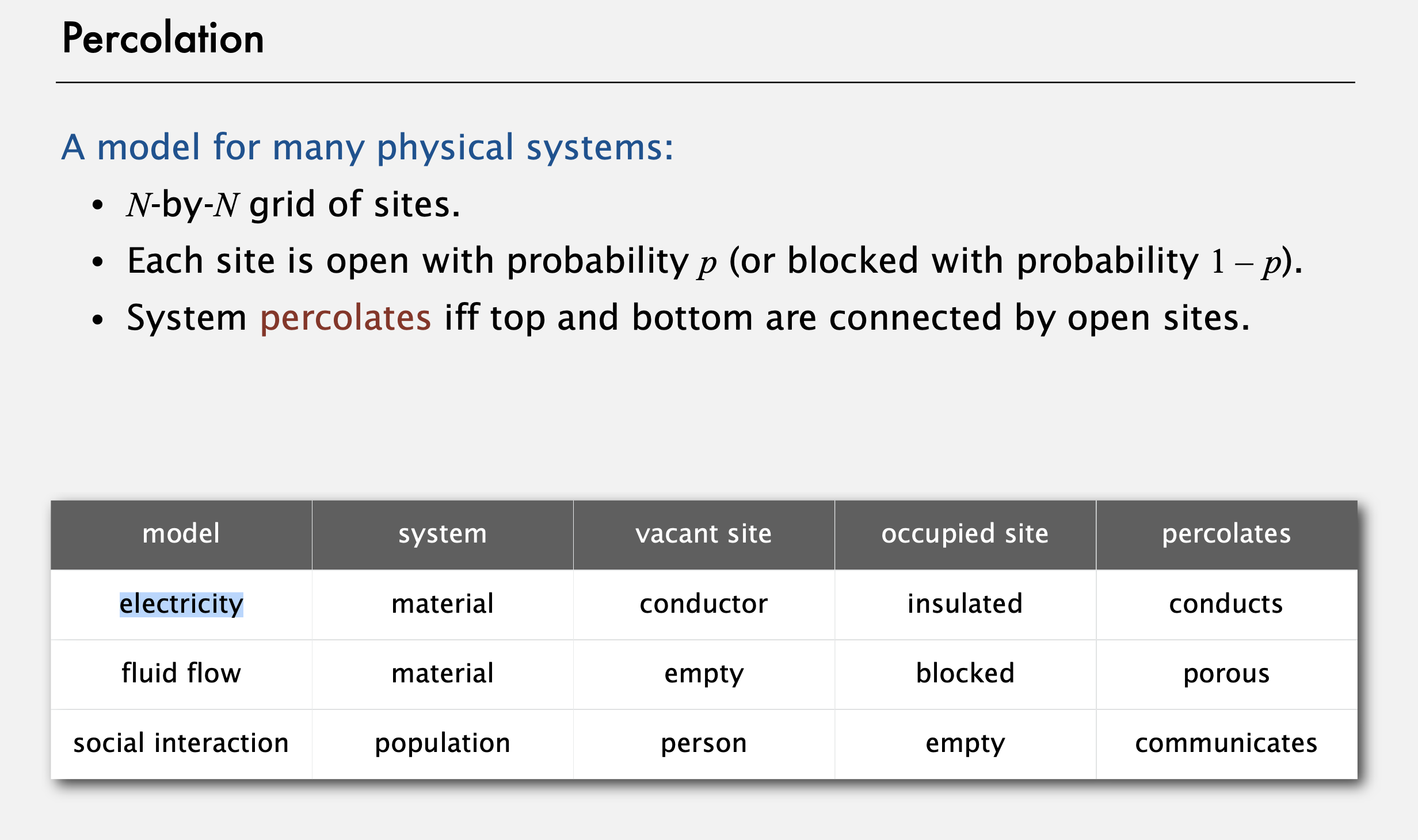
우선 전기(electricity)를 생각해 볼 수 있는데, 열린 장소(vacant site)를 전도체로 생각하고 막힌 장소(occupied site)를 절연체로 생각해보자. 그러면 상단에서 하단으로 이어지는 전도체가 있을 때 그 물체는 전기가 흐를 수 있다. 이러한 현상을 침투되었다 할 수 있다.
또 어떤 다공성 물질을 통해 흐르는 물을 생각해 보자. 열린 장소는 뚫려있고, 막힌 장소는 어떤 물질이 있다고 생각할 수 있고, 그 때 상단에서 하단으로 물이 흐를수도 아닐수도 있다. 이를 퍼콜레이션으로 생각할 수 있다.
또는 소셜 네트워크를 생각해 보자.소셜 네트워크에서는 사람들이 서로 연결되어 있는데, 두 사람을 선택하면 그 사람 간에는 연결이 있거나, 그렇지 않으면 없다. 한 그룹의 사람들이 다른 그룹의 사람들과 소셜 네트워크를 통해 의사교환을 할 방법이 있는지를 퍼콜레이션으로 생각할 수 있다.

이런것들은 퍼콜레이션 모델의 몇 가지 사례에 불과하다. 이제, 퍼콜레이션 모델 중에서도 랜덤화된 모델(randomized model)을 이야기할 것인데 이 모델에서는 각 장소가 특정 확률로 열림 상태일 수 있다. 그림 상의 왼쪽 예시들처럼 한 장소가 열릴 확률이 낮으면, 그 물리계는 침투되지 않을 것이다. 상단에서 하단으로의 연결이 만들어질 정도로 충분한 열린 장소들이 있지 않을테니까 말이다. 만약 확률이 높고 그에 따라 열린 장소들이 많다면 그 물리계는 분명히 침투될 것이다.
상단에서 하단까지 많은 길이 있을 테니까 말이다. 그러나 확률이 중간이라면, 침투될지 안 될지는 불분명하다. 따라서 이 모델에서 과학적, 또는 수학적 의문은, 이 물리계가 침투될 것인가 아닌가이다. 이 문제에서, 또 소위 상전이(phase transition)이라 불리는 많은 비슷한 문제들에서, 무슨 말이냐면, 확률이 낮을땐 침투되지 않을 거고, 확률이 높을 때는 침투될 거라는 것이다.
Percolation phase transition
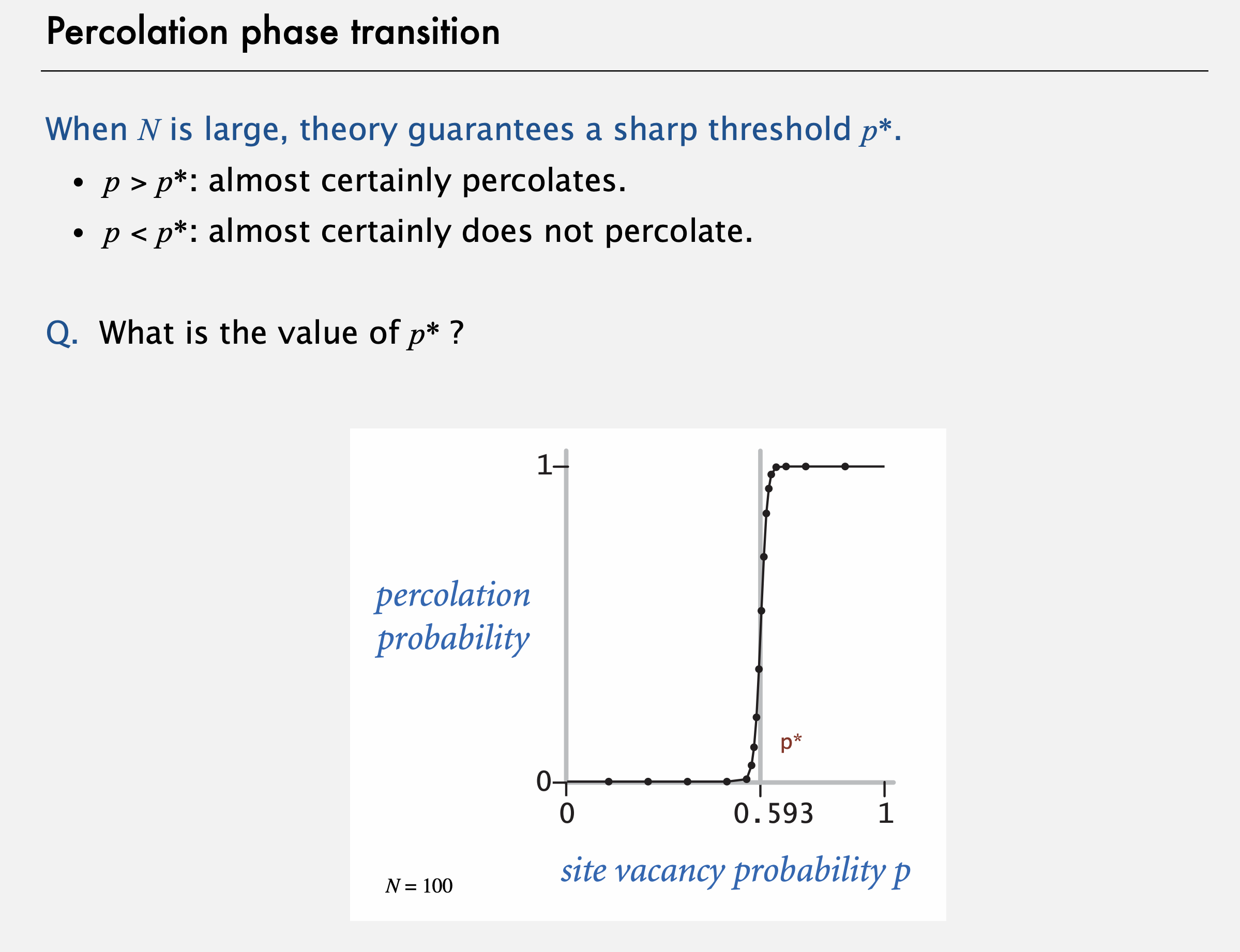
실제로도 침투 여부 사이에 있는 역치(threehold)를 그래프로 관찰해보면, 매우 가파른 변화가 일어난다. 그리고, 침투될지 안 될지에 대한 값 N이 존재한다. 그 값보다 작으면 거의 침투되지 않을 것이고 크면 확실히 침투될 것이다. 문제는 그 역치값이 무엇이냐는 것이다.
이 모델은 '역치값이 무엇인가'라는 문제가 매우 명확하게(articulated) 정리된 수학적 모델의 예시인데, 그럼에도 불구하고, 아무도 이 수학 문제에 대한 답을 알지 못한다. (역주: 증명할 수 있는 수학 공식으로 표현되는 답을 모른다는 의미) 답을 구하는 유일한 방법은 계산 모델(computaltional model)에 기반을 두는데, 그 확률에 대한 값을 결정하기 위해 시뮬레이션을 해야한다는 것이다. 그리고 그 시뮬레이션은 오직 quick union-find 알고리즘에 의해서만 가능한데, 바로 이것이 우리가 quick union-find 알고리즘이 필요했던 이유다. 그럼 한번 살펴보자.
Monte Carlo simulation

우리가 해보려는 것은 몬테 카롤로 시뮬레이션(Monte Carlo simulation)이라 한다. 이 시뮬레이션에서는 격자 상의 모든 장소를 막힘으로 초기화한 뒤, 각 장소를 확률에 근거해 무작위로 열림 상태로 변경한다. 이걸 계속 반복한다. 매 시각마다 열린 장소를 추가하고, 이 물리계가 침투되는지를 체크한다. 이를 물리계가 침투될 때까지 반복한다. 침투 될 시각의 열린 공간의 비율(vacancy persentage)를 구할 수 있는데, 침투가 일어나는 시각에서 측정된 이 비율은 역치값의 한 추정량(estimate)이다. 이러한 계산을 컴퓨터에서 해볼 만한 횟수인 수백만 번 정도 돌려 보는 것이다. 침투가 일어나는지의 여부를 효율적으로 계산함으로써 말이다.
이게 바로 몬테 카롤로 시뮬레이션이다. 아무도 수학적 모델로는 풀지 못한 과학적 문제에 대한 답을 주는 계산적 방법이다.
Dynamic connectivity solution to estimate percolation threshold
이제 퍼콜레이션 모델의 이해를 위해 동적 연결성 모델을 어떻게 활용할 지에 대해 좀 더 다루어보자. 명백히 각 장소에 대응하는 객체(=노드)를 만들어야 할 것이고, 우리는 여기 나타낸 것 처럼 0부터 N^2-1 까지로 명명할 것이다.

만약 열린 장소들 간에 연결되어 있으면 서로를 연결할 것이다. 그러면 왼쪽의 퍼콜레이션 모델은 우리가 계속 해왔던 것과 같이 오른쪽의 연결성 모델에 대응하게 된다. 이제 우리는 하단의 어떤 장소가 상단의 어떤 장소와 연결되어 있는지를 union-find를 활용해 알아보자고 말할 수 있다.
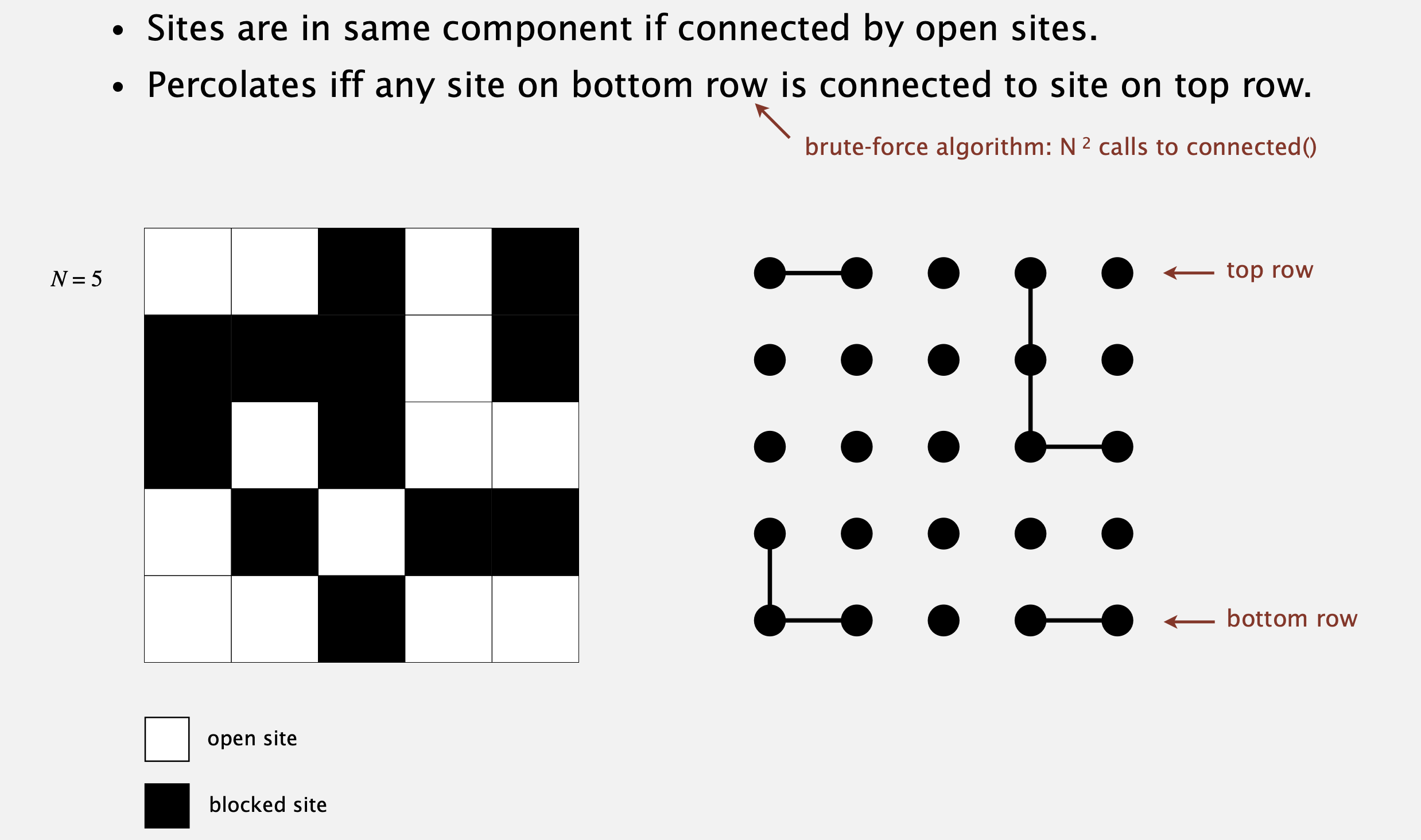
하지만 문제는 그 방법의 실행시간이 입력에 대해 이차함수로 증가하는 주먹구구식(brute-force) 알고리즘이라는 점이다. 연결 여부를 확인하기 위해 union-find를 호출하는 횟수가 N^2나 되기 때문이다. 상단의 각 장소와 하단의 각 장소를 모두 조합해 체크해야 하는데, 이는 너무 느리다.
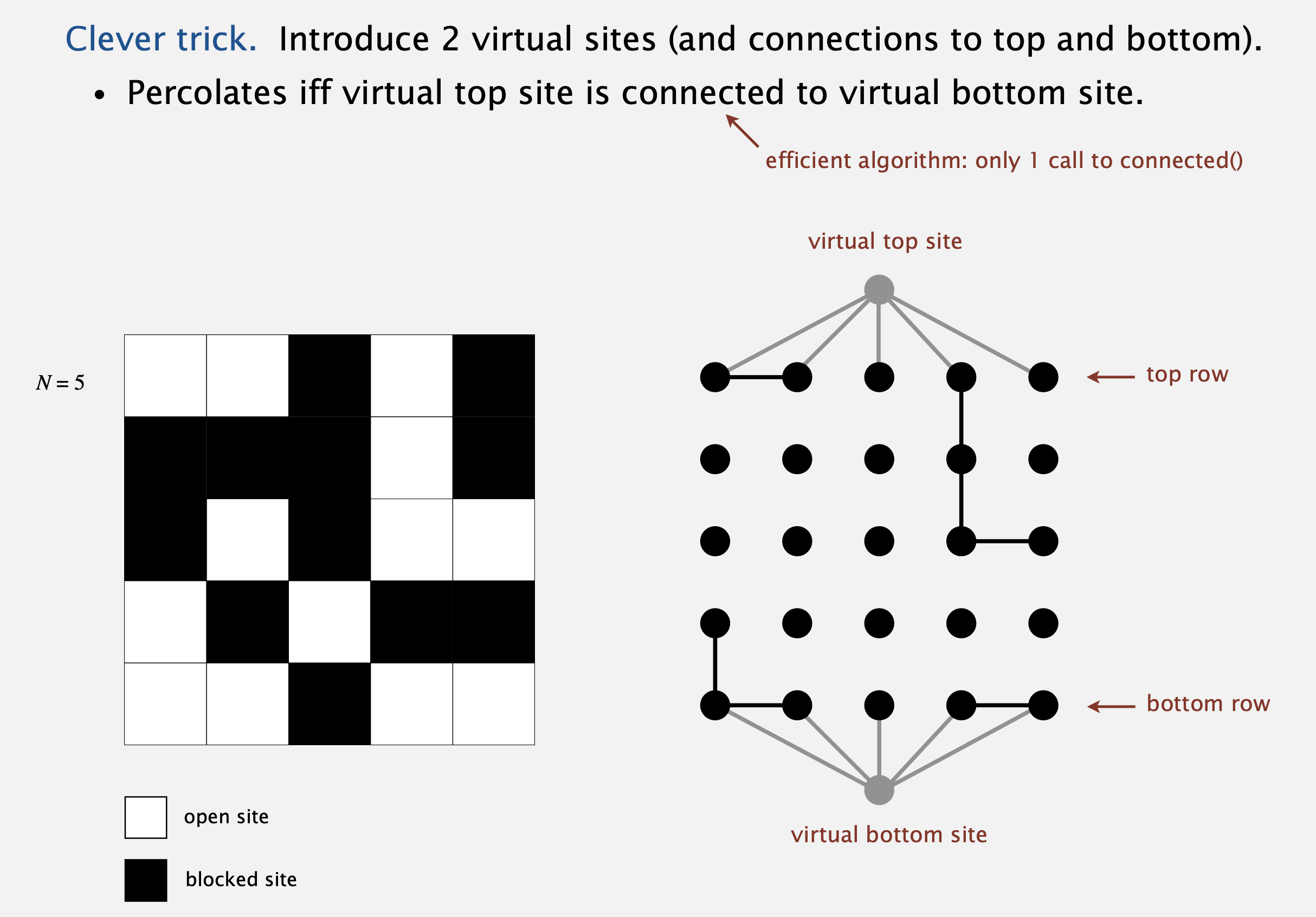
이와 달리 우리가 할 방법은 상단과 하단에 각각 가상의 장소를 생성하는 것이다. 이러면, 우리가 이 물리계가 침투되는지 알기 위해서 단순히 상단의 가상 지점과 하단의 가상 지점이 연결되어있는지 확인해보면 된다.
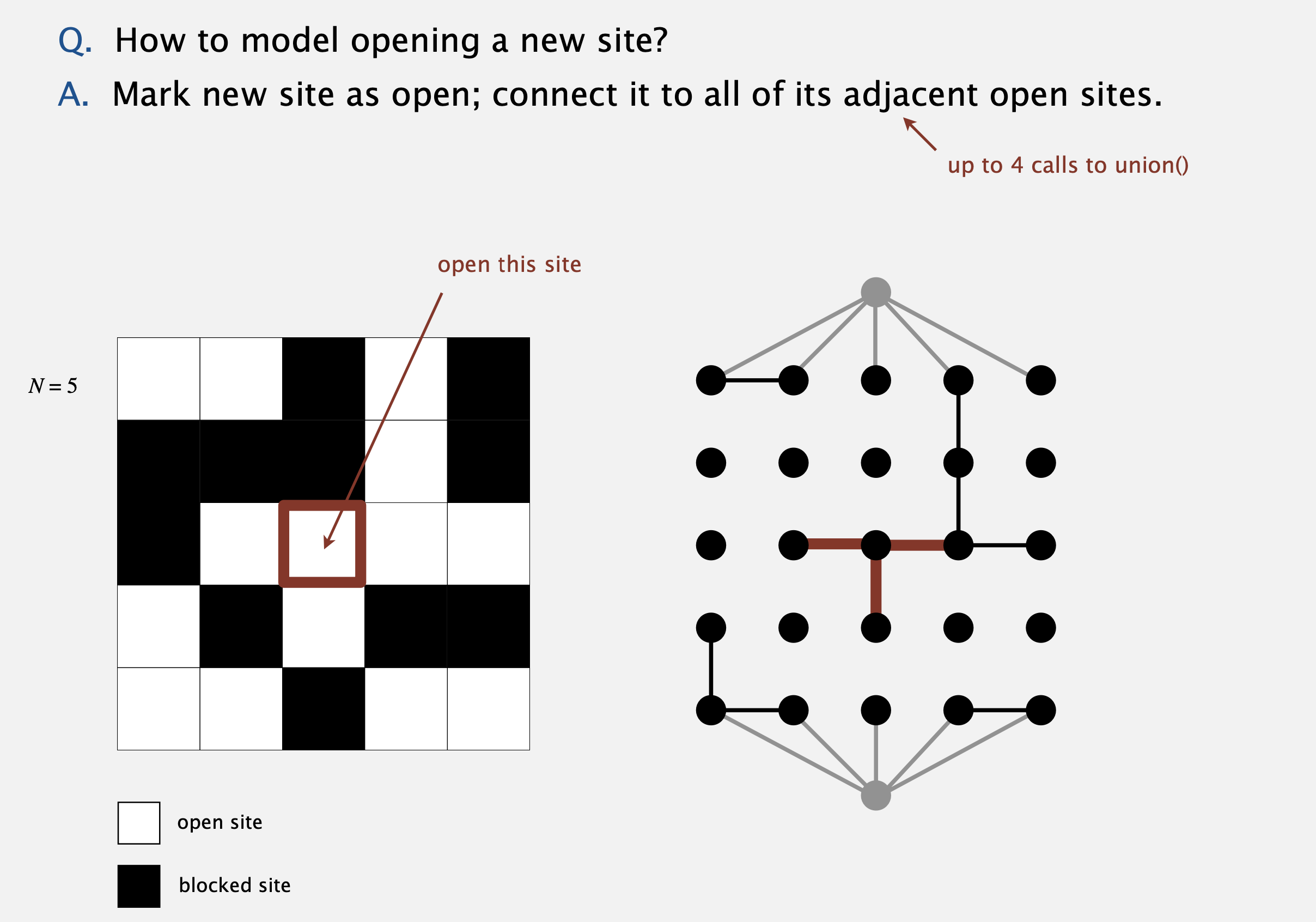
그럼 만약 어떤 장소를 열기 위해서 뭘 해야 할까? 장소를 열기 위해선 이웃한(adjacent) 모든 열린 장소와 그 장소를 연결한다. union 명령을 몇 번 호출해야 하지만 구현하기 쉽다.
Percolation threshold
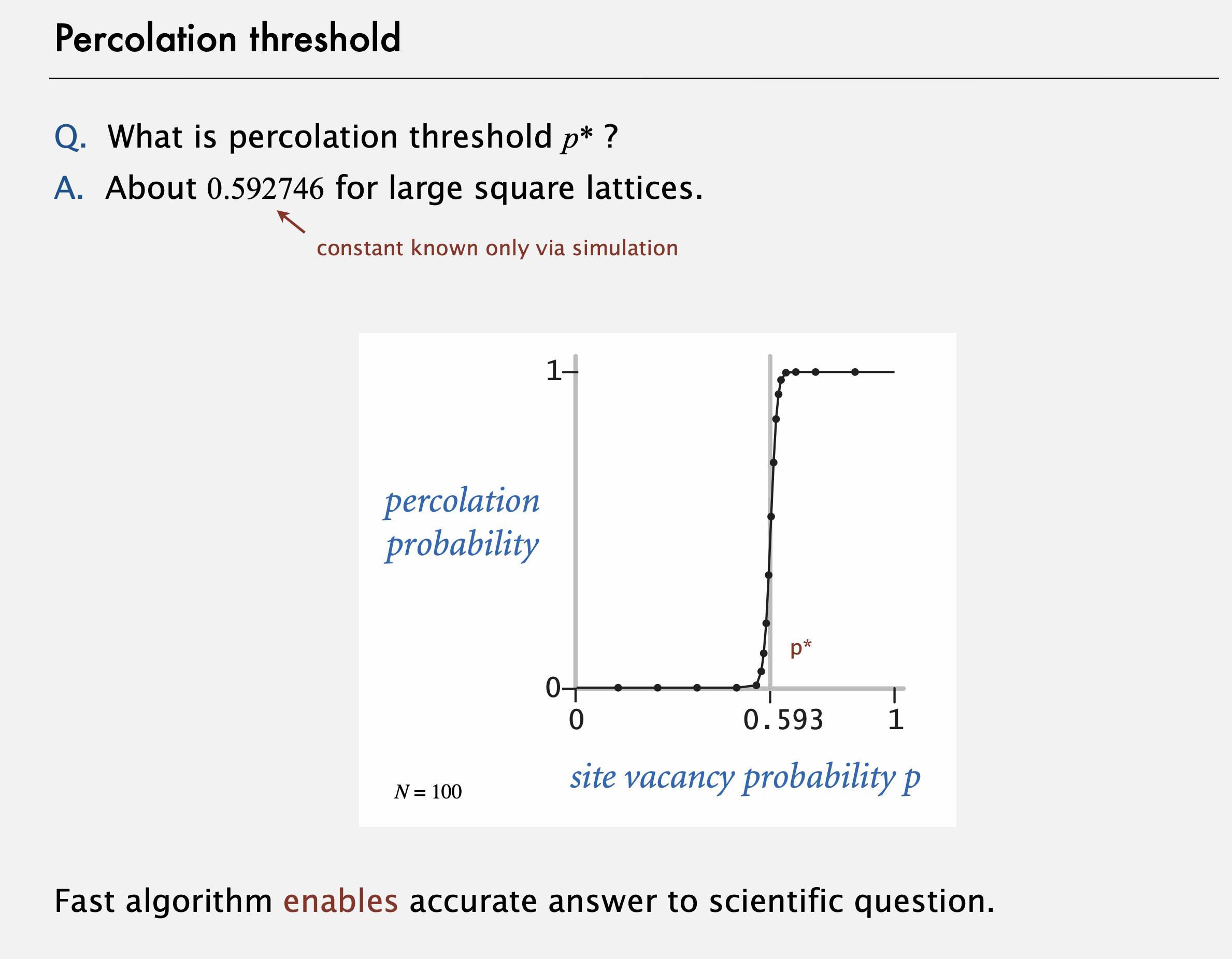
그 후 앞서 본 상관관계를 바탕으로, 우리가 앞서 개발해 온 코드를 활용해 이 연결성 문제를 시뮬레이션하는 데 사용할 수 있다. 그리고 충분히 큰 N에 대해 여러 번에 걸쳐 충분히 시뮬레이션을 거친 결과를 뽑아보면, 퍼콜레이션 역치값이 대략 0.592746임을 알 수 있다. 이 빠른 알고리즘으로 우리는 과학적 질문에 대해 정확한 답을 얻을 수 있다. 만약 우리가 느린 union-find 알고리즘을 사용한다면 크기가 큰 문제를 실행시킬 수 없을 것이고 매우 정확한 답을 얻을 수 없을 것이다.
정리
그래서 요약하자면, 중요한 문제를 배웠다. 동적 연결성 문제이다. 우리는 어느 자료구조와 알고리즘이 이 문제를 해결하기 위해 필요한지 정확하게 이해하기 위해 모델을 세웠고, 우리는 그 문제를 풀기 위해 몇 개의 쉬운 알고리즘을 먼저 보았고, 큰 문제를 다루기에는 부적절함을 보았다. 하지만 그 다음에 효율적인 알고리즘을 얻기위해 어떻게 향상시킬지를 보았다. 그리고 이런 효율적인 알고리즘 없이는 해결할 수 없는 응용들을 보았다.
이 모든 것은 과학적 방법을 수반하였다. 알고리즘 설계에서는 수학적 모델을 개발하려 노력해서 이는 우리가 개발한 알고리즘의 특징을 이해하는데 도움을 받았다. 그 후, 실험을 통해 모델들을 검사해보았고 이는 반복적으로 알고리즘을 개선시켜 더욱 세련된 알고리즘과 모델을 만들었다. 이는 결과적으로 우리가 관심을 갖는 실용 문제를 풀 수준이 되었고, 지금까지 정리한 알고리즘을 연구하는 전체적인 구조는 향후 모든 글 전반에서 활용될 것이다.
