이제 우리는 이 동적 연결 문제를 해결하기 위해 Quick-find라 불리는 알고리즘의 첫 번째 구현을 살펴보겠다.
Quick-find [eager approach]
이것은 연결 문제를 해결을 위한 조급한(eager) 알고리즘이라 불린다.
우리는 이 알고리즘을 위해 단순한 정수 배열로 된 객체를 자료구조로 사용할 것이다. 이 데이터구조에서 두 객체 P와 Q가 유일하게 연결되어 있다면 각 객체의 배열 인덱스 값은 동일하다. 그래서 아래 예제에서는
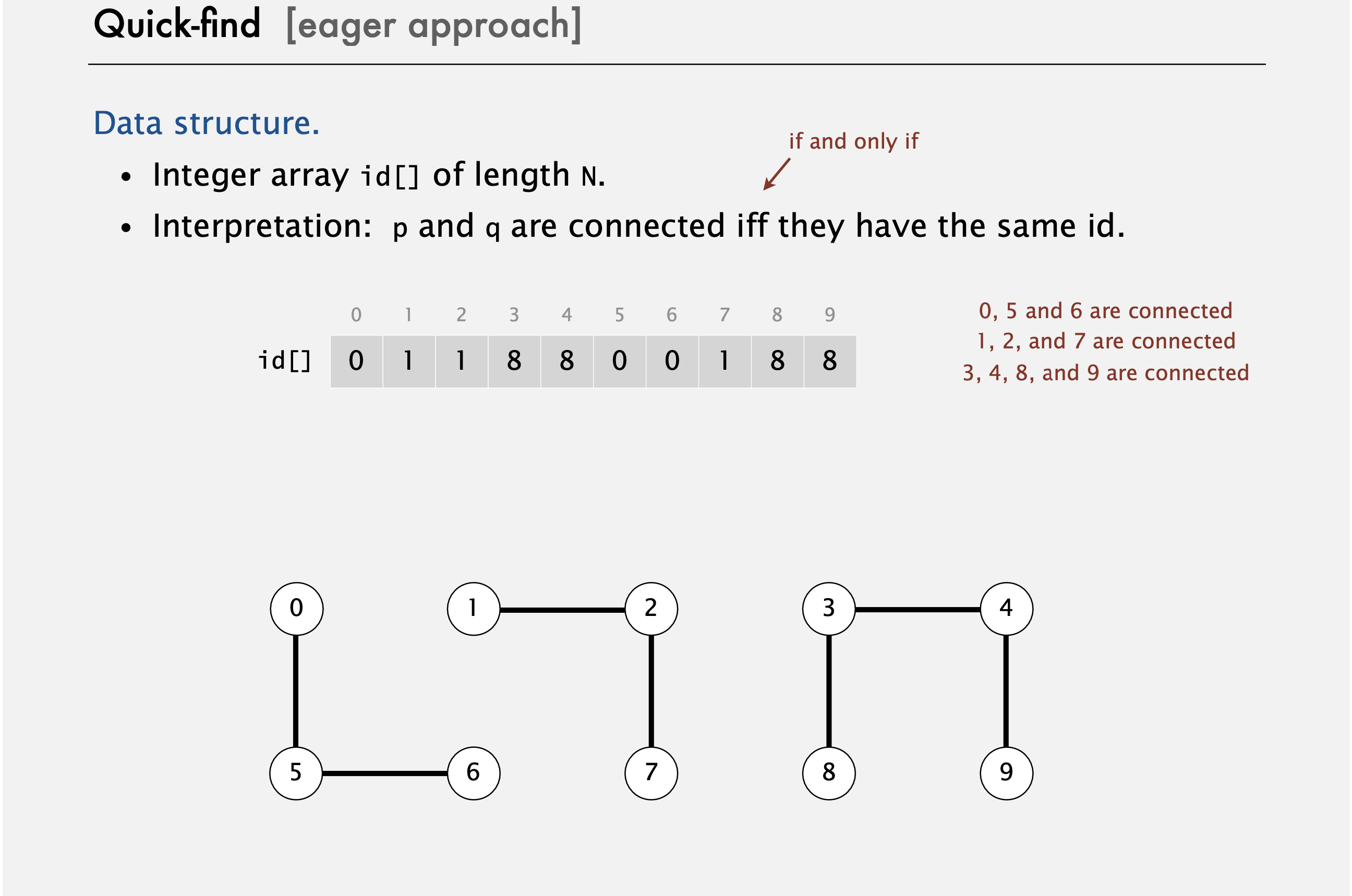
10개의 id 객체에 대해 7번의 연결(connection) 이후의 상황이 사진 중간에 나와있다. 여기서 보면 0, 5, 6 이 동일한 연결 컴포넌트(connected component)에 있는데 왜냐하면 세 개의 배열값이 동일하기 때문이다. 1, 2, 7은 모두 배열값이 1이고 3, 4, 8 그리고 9는 모두 배열값이 8이다. 그래서 여기 이것들이 모두 연결된 걸 보여준다. 그래서 명백히 이러한 구조가 find 연산을 빠르게 구현하는데 도움이 된다. 우린 그저 두 개의 배열값이 동일한지만 확인하면 된다.
p 와 q가 같은 id 값을 갖는지 확인해 보자.

첫 번째 배열은 값이 1이고 6번째는 값이 0이다. 이것들은 동일한 연결 컴포넌트가 아니다. Union은 주어진 두 객체의 배열 값을 합쳐야(merge)해서 좀 더 어렵다. 그러기 위해 같은 배열값을 갖는 모든 다른 배열값들을 바꿔야 한다. 그래서 여기서 우리는 임의로 p의 값과 같아지도록 바꿀지 q의 값과 같아지도록 바꿀지 정해야 한다. 만약 6과 1을 union 하려고 한다면 0 번째, 5번째 6번째 배열값을 바꿔야한다. 이것들은 모두 6번째 배열과 같은 연결 컴포넌트에 있는데 배열값 0을 1로 바꿔야한다. 지금 본 것처럼 이런 방식은 매우 큰 객체를 다룰 때 문제가 된다. 왜냐하면 바꿔야 할 값들이 너무 많기 때문이다. 하지만 구현이 쉬우니까 일단 여기서 시작하자.
우선 이게 어떤 식으로 동작하는지 논리적으로 작성해보자.
먼저 우리는 모든 id 배열값을 각자의 배열 인덱스로 초기화한다. 그래서 모든 배열 객체는 독립적이다. 각 배열은 각각의 연결 컴포넌트에 있는것이다.
이제 union 연산을 하게되면, 즉union(4, 3)을하면 우린 첫번째 인자의 배열값을 두번째 인자의 배열값으로 바꾼다. 여기서 3과 4를 연결한다는 것은 4번째 배열의 값을 3으로 바꿔야한다. 동작 원리를 이해할 수 있도록 몇개 더 해보자. 이제 union(3, 8)이다. 3번과 8번을 연결하기 위해서 3, 4, 8이 연결되어야 한다. 그래서 3,4 배열값이 8로 바뀌어야한다.
그러면 union(6, 5)는 어떨까? 첫번째 인자의 배열값을 두번째 인자로 바꾼다. 그래서 6번과 5번을 연결하기 위해 6번 배열값을 5로 바꾼다. union(9, 4)또한 9번 배열값을 4번과 같게 바꿔야 한다. 그래서 이제 3, 4, 8, 9번을 보면 모두 배열값이 8이다. 이것들은 모두 동일한 연결 컴포넌트에 있다. union(2, 1)은 2번 배열값을 1번 배열값인 1로 바꾸는 걸 의미한다. union(8, 9)는 이미 연결되어 있기 때문에 이 두개는 이미 id 배열 값이 같다. 그래서 connected 함수 질의에 이미 연결되어 있으므로 true로 나온다. connected(5, 0)은 다른 배열값을 갖는다. 이 둘은 연결되어 있지 않다. 그래서 false를 리턴할 거고 그럴 경우 연결되지 않은 것이다. 만약 5번과 0번을 연결하고자 한다면 관련있는 5번과 6번의 배열값 모두를 0으로 하면 된다. 7번과 2번을 union하는건 7번 배열값만 2로 바꾸면 되기때문에 아주 쉽다. 그리고, union(6, 1)은 3개의 값이 바뀌어야 한다. 모든 배열값 0이 1로 바뀌어야 한다. 이 작업들의 결과는 다음과 같다.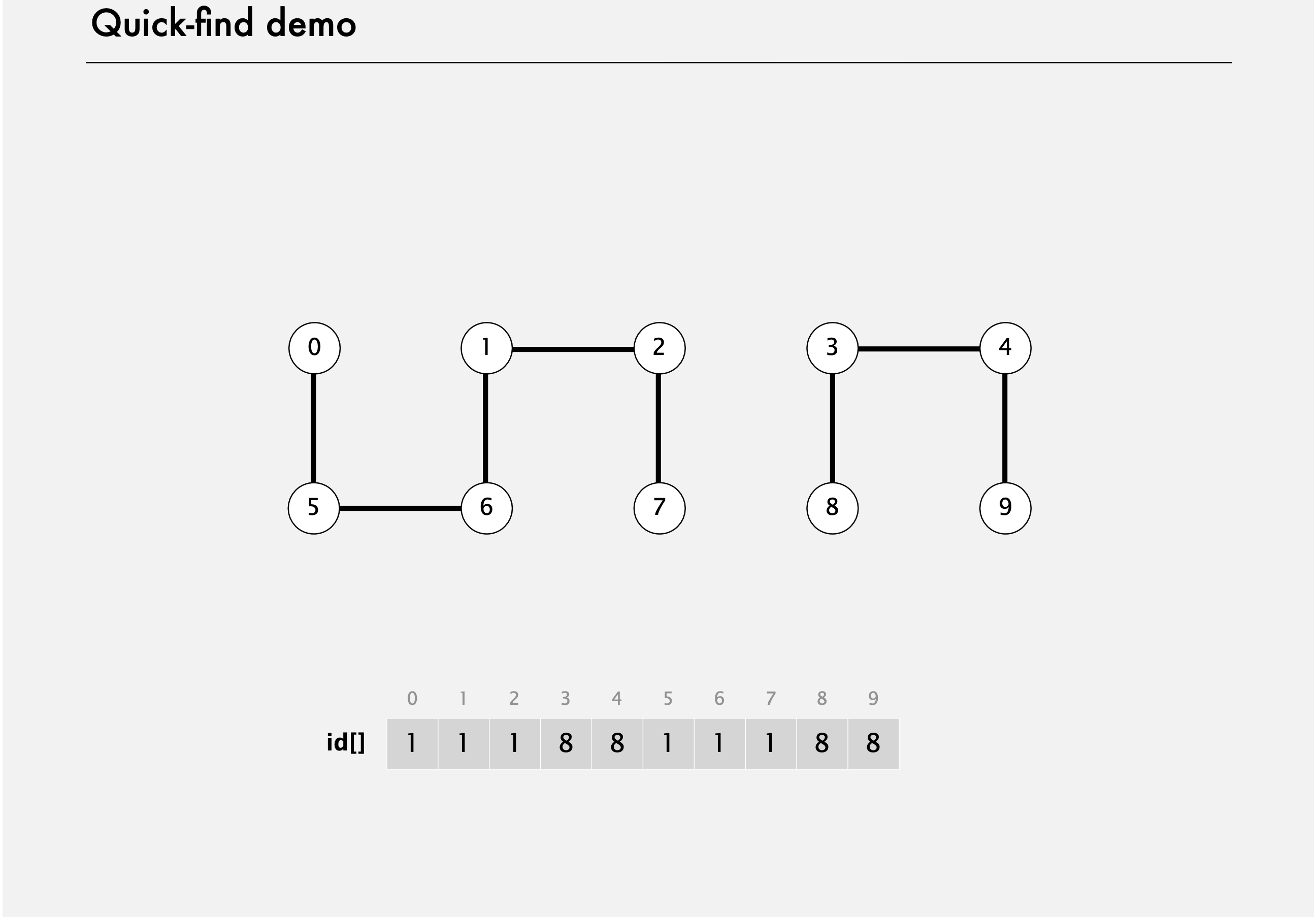
이제 다음으로 이것에 대한 구현을 보겠다.
Quick-find: Java implementaion
이 알고리즘을 짜는 것은 매우 쉬울 것이다. 하지만 대부분이 처음엔 실수하는게 프로그래밍 연습의 재미다. 자, 생성자부터 시작해보자. private 정수 배열이 있다. 이게 id 배열이다. 우리가 구현할 부분을 위한 자료 구조이다.

생성자는 배열을 초기화 해야하고 계속해서 각 배열 인덱스 i로 배열 값을 세팅해야 한다. 이건 수월한 작업이다. find 또는 connected 구현은 아주 쉽다.

이것이 Quick-find 알고리즘이다. 그래서 단순히 두 인자 p 와 q를 받아서 id 배열값이 같은지 비교하고 그 값을 리턴한다. 같으면 true를 리턴하고 다르면 false를 리턴한다.
좀 더 복잡한 구현은 union 이다.
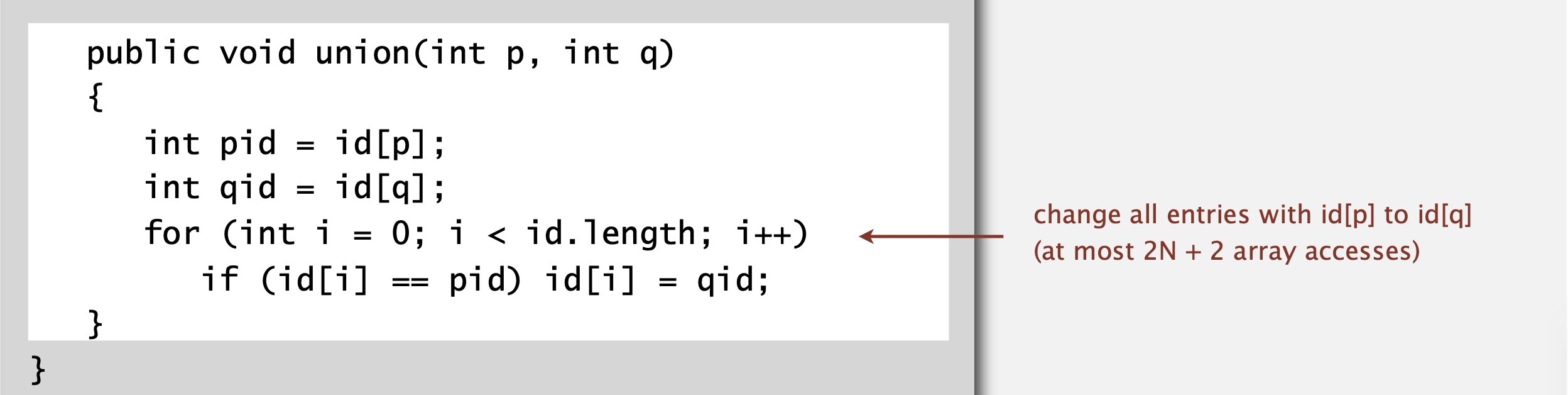
여기서 우린 첫번째 인자에 대응하는 배열값을 찾고 이어서 두번째 인자에 대응하는 배열값을 찾는다. 그리고 전체 배열로 부터 첫번째 인자의 배열값과 같은 값을 찾는다 그리고 그것을 두번째 인자의 배열값으로 세팅한다. 이건 상당히 뻔한 구현인데 이전에 언급했듯이 많은 사람들이 여기서 실수를 한다. 그건 바로 pid부분에 p의 배열값 대신에 p 값을 넣는 것이다. 이 문제를 해결할 때 이 코드의 의미에 대해 생각해 봐야한다. 그건 잠재적인 버그이다.
Quick-find is too slow (너무 느리다)
이것으로 QuickFind 구현을 봤고 다음으로는 이 알고리즘이 얼마나 효율적일지 결정해야 한다. 그리고 어떻게 그렇게 할지 자세히 얘기할 것인데 그런데 그건 단지 코드에서 배열에 얼마나 많은 횟수로 접근해야 하는지만 생각해도 충분하다. 우리가 구현하면 봤듯이, 초기화와 union 함수에서 모든 배열을 순회하도록 되어 있다. 그러므로 배열값에 접근한 뒤 상수 비율로 N번 접근해야 한다.
find 연산은 빠르다. 이건 단지 배열값을 확인하는 상수 시간이 걸린다. 그런데 여기서 union 연산이 너무 비싼게 문제이다. 특히 일반적이지 않지만 만약 N개의 객체에 대해 N 번의 union을 한다고 가정해보자. 이 동작은 이 객체들이 모두 연결되는 아니든 제곱시간 만큼 걸릴 것이다.
그리고, 앞으로 우리가 계속해서 보게 될 테마 중 하나가 제곱시간(quadratic time)은 정말 느리다는 것이다. 그래서 우리는 아주 큰 문제에 대해서는 제곱시간 알고리즘을 받아들일 수 없다. 왜냐하면 그런 알고리즘은 확장성이 없기 때문이다. 컴퓨터가 더욱 빠르고 클수록, 제곱시간 알고리즘은 실제로는 더 느려진다. 이제 이 말이 무슨 의미인지 간단히 얘기해보자.
Quadratic algorithms do not scale
요즘 일반적으로 사람들이 가진 컴퓨터는 1초에 수십억개의 명령을 처리할 수 있다. 그리고, 메인 메모리에 수십억개의 인자를 저장할 수 있다. 즉, 이건 컴퓨터들이 1초내에 메인 메모리에 있는 모든 인자를 건드릴 수 있다는 의미이다. 대략적인 성능 기준이 이 수준에 이르는 데까지 겨우 50~60년 걸렸다는 건 놀랄만한 사실이다. 컴퓨터의 메모리가 계속 커지지만, 빨라지기도 하니 메모리의 모든 자료에 접근하는 것은 몇 초가 걸릴 것이다. 컴퓨터가 오직 몇천 개의 워드를 메모리에 저장할 수 있었던 시기가 있었고 현재는 몇십억 개 혹은 그 이상을 저장할 수 있는 것이 사실이다.
요즘 컴퓨터가 이렇다는 것을 받아들이자. 이 뜻은, 우리는 저 큰 메모리를 이용해 거대한 문제를 다룰 수 있다. 그래서 우리는 수십억 개의 객체들을 사용할 수 있고, 수십억 개의 Union 연산이 메모리 위에서 동작하길 바랄 수 있다. 하지만 quick find 알고리즘의 문제점은, 그 알고리즘은 10^18제곱 번의 연산을 하거나 혹은 그만큼의 메모리에 접근해야 한다는 것이다. 그리고 만약 계산을 해보면, 컴퓨터로 30여 년이 걸린다는 것을 계산할 수 있다. 명백히, 오늘날의 컴퓨터로는 현실적으로 다룰 수 있는 문제가 아니다. 그리고, 그 이유는, 실행 시간이 입력 크기 N의 제곱에 비례하는 이차함수를 따르는 알고리즘은 기술적으로 N을 키울 수 없기 때문이다. 내가 10배 더 바른 새로운 컴퓨터를 가지고 있더라도 나는 10배 더 큰 문제까지만을 다룰 수 있다. 그리고 내가 실행시간이 이차함수를 따르는 알고리즘을 다룬다면 10 배 더 느려진다. 이런 상황이 우리가 효율적인 알고리즘을 발전시킴으로써 피하고자 하는 상황이다.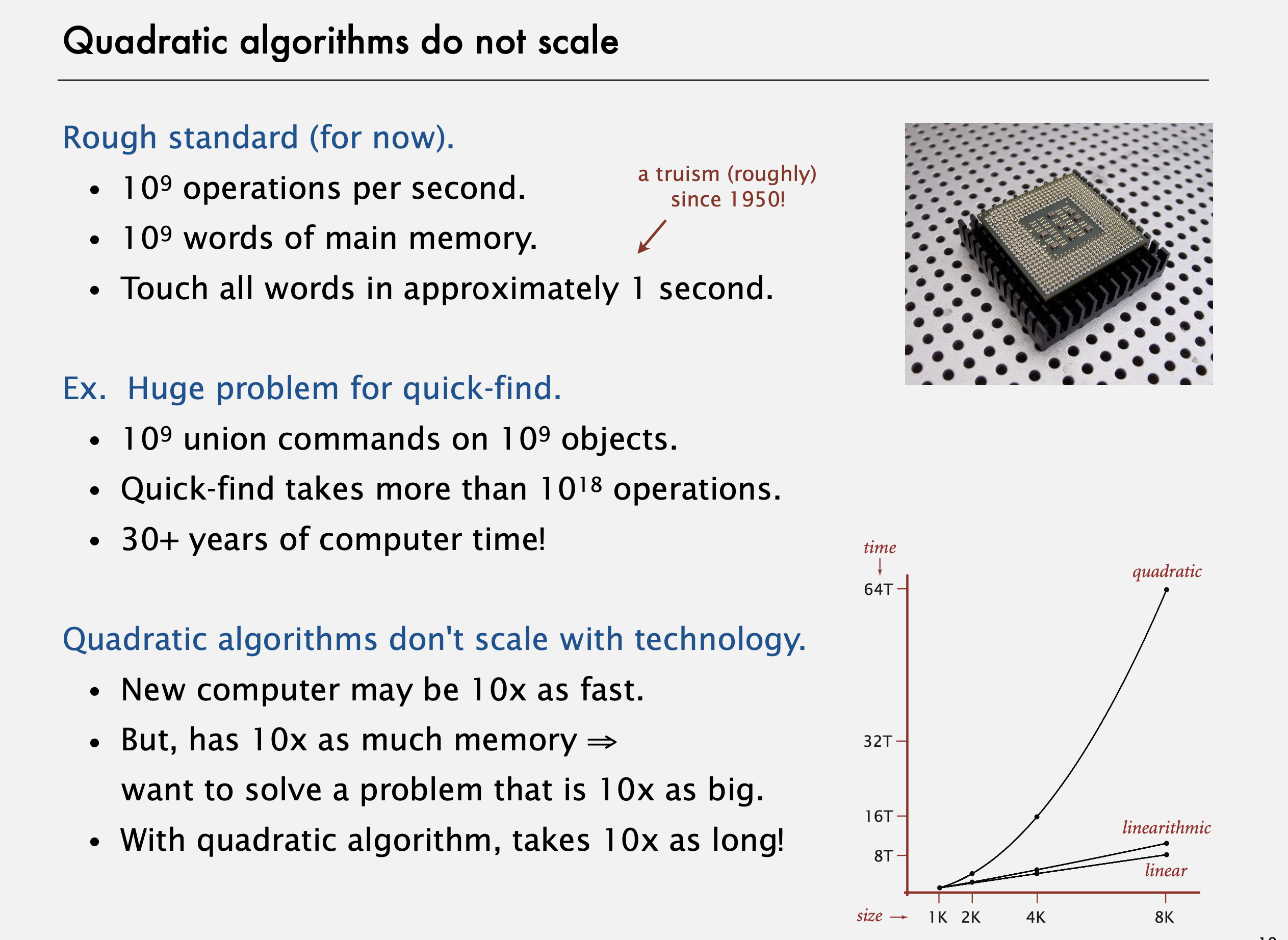
해당 문서는 링크를 보고 공부한 내용을 정리한 글입니다.
coursera
