이 문제에서 소위 동적 연결성(dynamic connectivity) 문제를 푸는 몇 가지 알고리즘이 있다. 우리는 Quick Find/Quick Union이라는 두 개의 고전 알고리즘을 살피고, 이 알고리즘들의 응용사례와 성능 향상법을 살펴본다. 그 전에 먼저 유용한 알고리즘을 개발하기 위해 반복해서 따라야 할 단계들을 알아보자.
유용한 알고리즘을 개발하기 위한 단계
이 단계에서는 풀 필요가 있는 문제의 주요 요소들이 무엇인지를 기본적으로 이해해야 한다. 그럼 문제를 풀 몇몇 알고리즘을 떠올릴 수 있다. 많은 경우에, 우리가 처음 떠올린 알고리즘은 (그럭저럭 사용하기에) 충분히 빠르고 메모리 문제도 없을 것이라서, 그냥 사용하면 원활히 돌아간다 (off and running). 하지만 어떤 경우들엔 빠르지 않거나 메모리가 부족하다. 따라서 우리의 할 일은 왜 그런지 이해하고, 그 문제를 야기하는 모든것을 찾아내고, 새 알고리즘을 발견해 만족할 때까지 이 과정을 반복해야 한다.
이러한 방법은 알고리즘을 만들고 분석하는 '과학적 접근 (scientific approach)'인데, 여기서 이렇게 돌아가는 상황을 시도하고 이해하는 수학적 모델을 설계하고, 이러한 수학적 모델을 입증하는 실험을 통하여 더 나은 알고리즘을 만드는 데 도움을 받을 것이다.
동적 연결성 문제
동적 연결성 문제는 union-find 문제에 대한 추상적인 모델이다. 아이디어는 다음과 같다.
N개의 객체가 모여있다고 하자. 각각이 무엇인 지는 중요하지 않다.
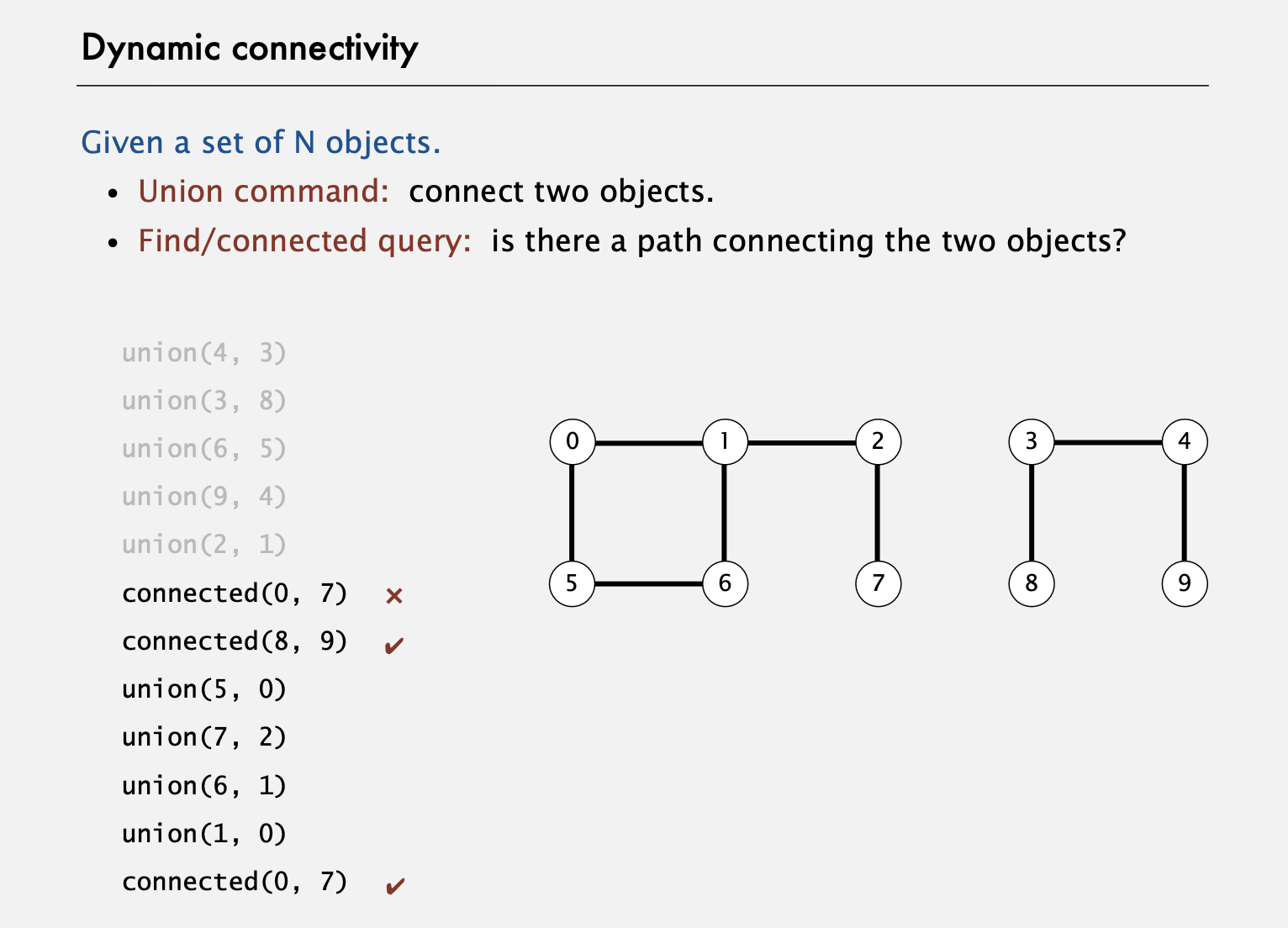
이 N개의 객체에 0부터 (N-1까지) 번호를 붙인다. 그리고 두 객체 간의 연결을 만들어보려 한다. 이를 위해 이런 명령어가 있다고 상정해본다. "두 객체를 연결(connect)해라."는 식의. 이 명령어는 두 객체가 주어지면, 그 둘의 연결을 만든다. 이제 이 문제의 본체는 두 객체를 연결하는 경로(path)가 있는지를 답하는 Find 'connected(?,?)'라는 질의(query)를 찾는 것이다. 예로 사진에 나오는 10개의 객체가 모여있을 때, 몇 개의 'union(?,?)' (연결하라는) 명령을 생각해보자.
3, 4, 8, 9와 5, 6과 1, 2를 연결해보자. 이제 0과 7이 연결되어 있는지를 답하는 'connected(0,7)'질의를 생각해보자. 자, 이 경우엔 연결이 없으니 '아니오'라고 답해야 한다. 하지만 8과 9가 연결되어있는지를 묻는다면? 이제는 '예'라고 답해야한다. 8과 9 사이에 직접적인 연결은 없지만 8, 3, 4, 9를 따라서 경로가 있기 때문이다. 따라서 '주어진 객체 집합에 대해 두 명령어를 정식으로 지원하도록 하는 것'이 우리의 문제이다. 이제 5, 0을 union하라는 명령을 추가하면, 5와 0사이에 연결이 생기고, 7과 2도 union하면 둘 사이에 연결이 생긴다. 그리고 6과 1도 연결해보자. 그리고 불필요한 연결이지만 1과 0도 연결해보자. 그러면 이제 0과 7이 연결되어있는지를 물으면 '예'라고 답해야 한다.
이게 union 명령과 connected 질의를 섞어진 것이 우리가 풀고자 하는 문제이다. 수많은 객체가 주어졌을 때 이 명령어들을 정식으로 지원할 수 있어야 한다. 이제 더 큰 문제를 생각해보자.
Connectivity example
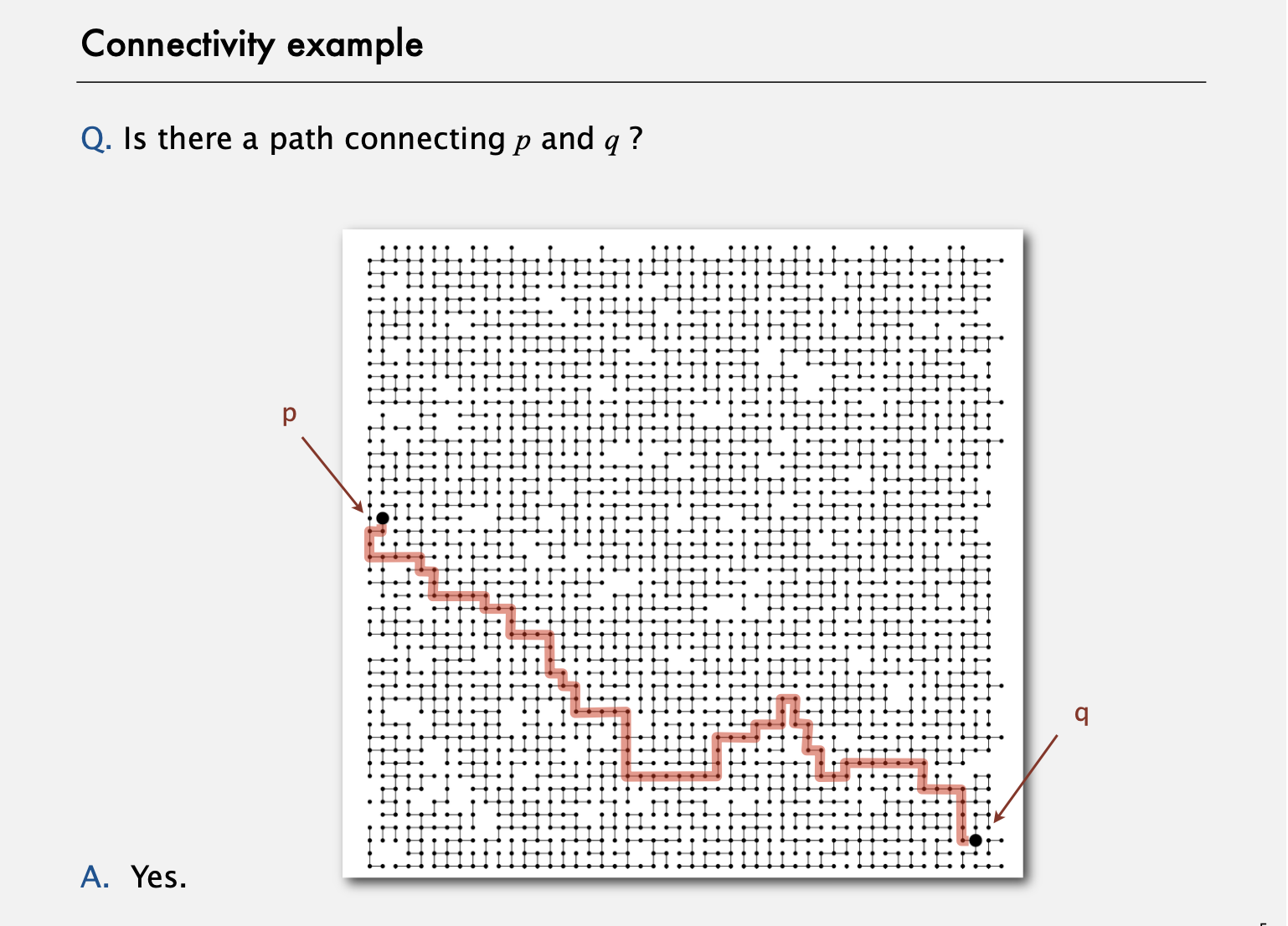
보이듯이 이를 풀기 위해선 효율적인 알고리즘이 필요하다.
주어진 그림에는 연결이 있다. 오늘 살피려고 하는 알고리즘은 두 객체를 연결하는 경로를 답하는 게 아니다.
그냥 경로가 있는지에 대해 (예 혹은 아나ㅣ오로) 답하는 거만 하면 된다. 나중에 part2에서는 경로를 명확히 찾아내는 알고리즘들을 고려할것이다. 그 알고리즘들을 위해서는 할 게 많아서 union-find 알고리즘만큼 효율적이진 않다.
동적 연결성 알고리즘의 응용 사례
어떠한 객체에라도 이 알고리즘을 적용할 수 있다. 객체가 픽셀들로 이루어진 사진 파일에 사용할 수도 있고, 컴퓨터가 객체인 네트워크에도 사용가능하고, 사람을 객체로 간주한 소셜 네트워크에나, 회로 요소를 객체로 간주해 컴퓨터 칩에도 사용가능하고, 프로그램에서 추상화된 것들을 객체로 간주해볼 수 있다. 이를테면 프로그램 내의 변수 이름이나, 수학에서 말하는 집합에서의 원소를 객체로 볼 수도 있다. 또는 컴포지트 시스템에서 금속재 배치 같은 게 있다. 이런 서로 다른 객체에 대한 타입과 상관없이 프로그래밍 할 때에는 각 객체에 이름을 붙이면 될거고 우린 0에서 N-1까지의 정수처럼 숫자로 붙여본다. 이렇게 시작하는 건 프로그램을 생각할 때 매우 편리한데, 각 객체를 나타내는 정수를 배열의 인덱스로 사용할 수 있기 때문이다. 이 때문에 각 객체와 관계된 정보에 빨리 접근할 수 있다. 또한 union-find 알고리즘과 관련없는 수많은 상세를 숨길 수 있다.
사실 이렇게 객체명을 0에서 N-1 까지의 숫자에 매핑(mapping;사상)함으로써, 심볼 테이블이나 검색 알고리즘에의 적용도 가능하다. 이것들은 추후 다른문제들을 푸는 알고리즘과 자료구조를 다룰 때 배우게 될 것이다.
모델링
이제, 앞에서 다룬 '연결'이 만족해야 할 추상적인 몇몇 성질들을 모델링할 필요가 있다. 우리가 모델링할 이 성질들은 자연스럽고 직관적이다. 먼저 우리는 (보통 이산수학 시간에 다루는) 'A가 B에 연결되어 있다(A is connected to B)'라는 표현을 '동치 관계(equivalence relation)'로 가정한다.
먼저, 모든 객체는 자기 자신에 연결되어 있다. 다음으로 이 표현은 반사적(symmetric)이다. P가 Q에 연결되어 있으면 Q도 P에 연결되어 있다. 그리고 대칭적이다. P가 Q에 연결되어 있고 Q도 R에 연결되어 있으면 P는 R에 연결되어 있다. 이런 성질들은 매우 직관적이다. 하지만 알고리즘을 명확하게 유지하기 위해서는 명확하게 말할 필요가 있다.
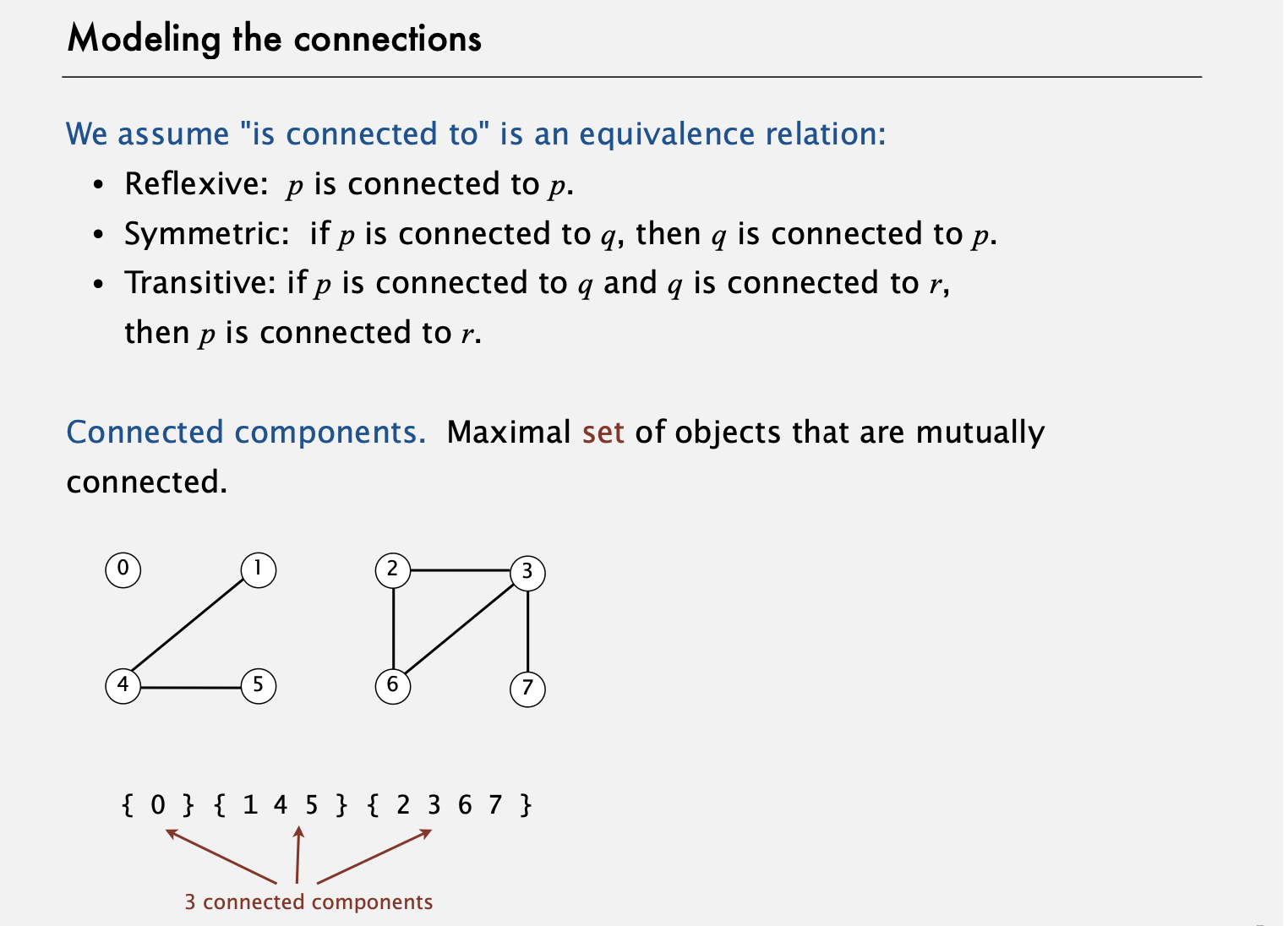
이제 우리가 객체의 집합과, 연결 요소들(connected components)이라고 불리는 부분집합들로 그 집합을 나누는 연결로 이루어진 동치 관계를 갖는다. 연결 요소는 상호적으로 연결된 객체들의 최대 집합(maximal set)이다. 이를테면 여기 이 작은 예에선 세 개의 연결 요소가 있다. 0으로만 이루어진게 하나, 1, 4, 5로 이루어진게 하나, 나머지 4개 객체로 이루어진 게 하나로 세 개 이다. 이 연결 요소들은 그들 중 어느 두 객체가 연결되어 있으면 그 두 객체와 외부에서 연결된 요소는 그 연결요소 밖엔 없다는 성질을 갖는다. 이를 연결 요소라 부른다. 우리 알고리즘은 연결 요소를 유지함으로써 효율성을 갖는다. 또한 이러한 지식을 통해 효과적으로 여기서 살펴보고 있는 질의에 답할 수 있게 된다. 이제 연산(operation)들을 구현해보자.
연산 구현
해야될 건 (지금까지의 지식으로) query와 union 명령을 구현하는 것이다. 여기서 우린 연결 요소들을 명령이 계속 주어져도 유지할 것이다. 먼저 find 질의는 동일한 연결 요소에 있는지를 체크하는 것으로 바뀌게 되고, 다음으로 union 명령어는 두 객체를 포함하는 연결 요소들의 합집합으로 연결 요소들을 대체해야 하게 됩니다. 이제 예를 들어, 이와 같은 열결 요소들이 있다고 하고, union(2,5)라는 명령을 주면, 연결이 되면서 2를 포함한 연결 요소와 5를 포함한 연결 요소를 합칠 필요가 있다.
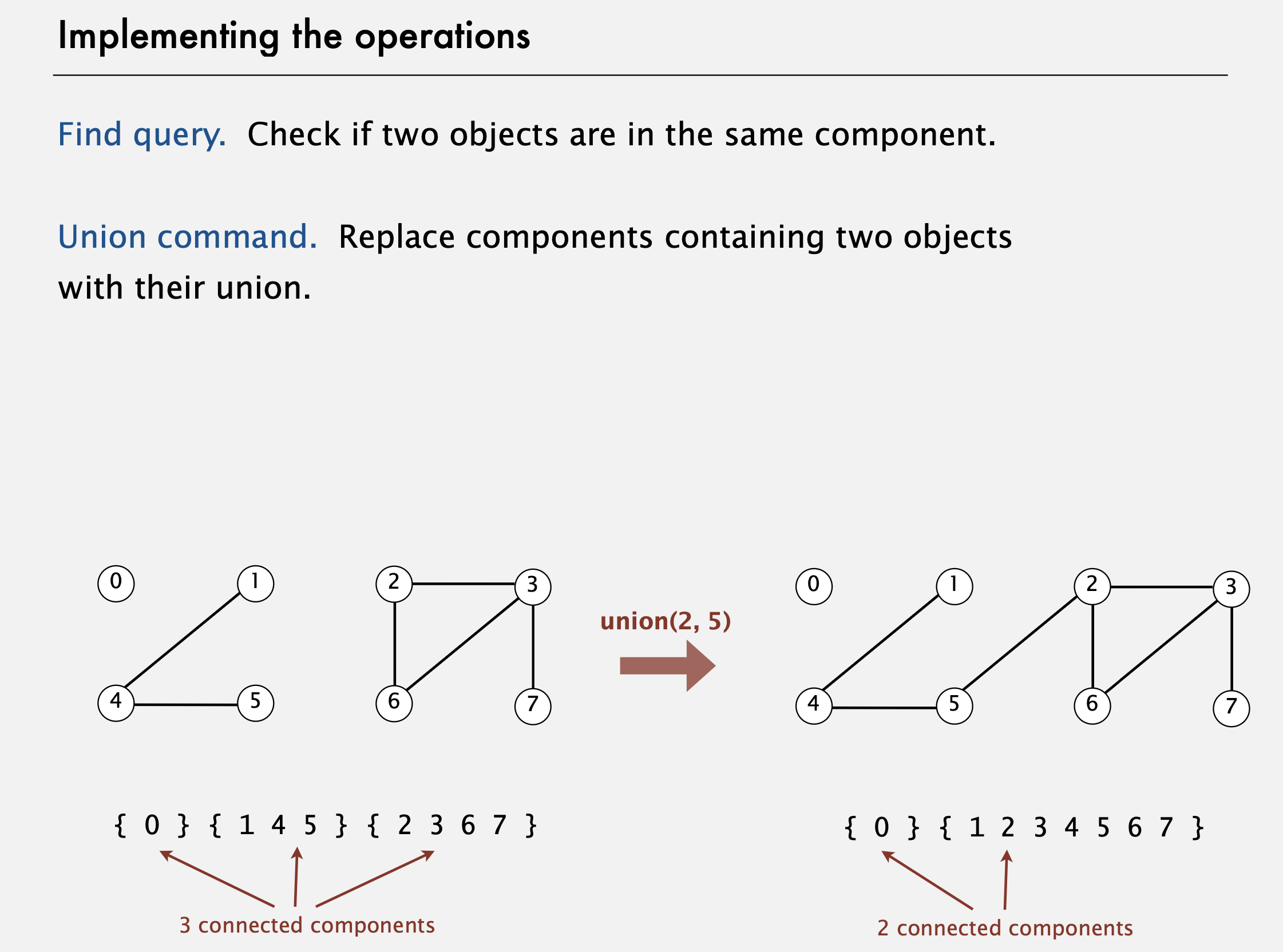
이를 통해 더 큰 연결 요소를 만들게 되고 이제 연결 요소는 3개에서 2개로 줄었다.
Union-find data type (API)

이런 것들을 하기 위해서 프로그래밍 세계에서는 데이터 타입을 명시해야 한다. 이는 문제를 풀기 위해 구현할 필요가 있는 메소드들을 명시하는 것도 포함한다. 우린 전형적인 Java 모델에 따라서, union과 connected라는 두 메소드를 갖는 UF라는 클래스를 만들 것이다. 여기서 connected는 boolean 타입을 리턴한다. 생성자(constructor)는 객체의 수를 받아서 객체의 수에 기반한 자료 구조를 만들게 된다. 명심해야할 것은 알고리즘을 설계할 때, 객체의 숫자도 많을 수 있지만 연산의 수도 많을 수 있다는 것이다. 우리는 이제 매우 많은 수의 union과 connected 연산을 하고 우리의 알고리즘이 그러한 상황에서 효율적이 되도록 만들 것이다.
Dynamic-connectivity client
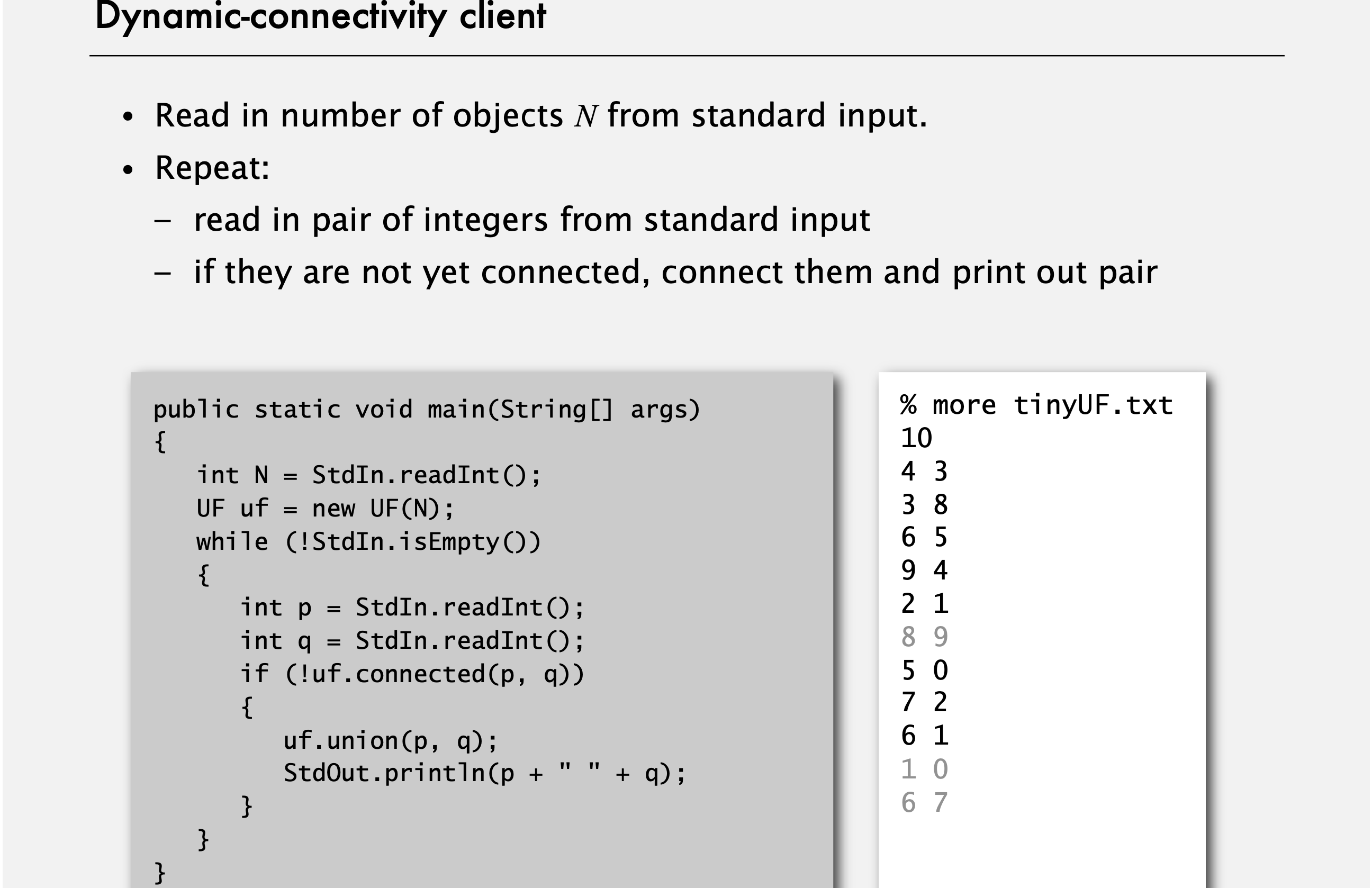
여기서 때때로 주어질 숙제로, 문제를 깊이 다루기 전에 우리의 API 설계를 체크해보자. 즉, 우리가 개발한 데이터 타입을 사용한 클라이언트 프로그램을 만들어보자. 이 예에서는, 클라이언트 프로그램이 표준 입력으로 정보를 받는다. 먼저 우리가 처리할 객체의 수를 정수로 받고, 일련의 객체명 페어를 받는다. 그러면 클라이언트 프로그램을 먼저 표준 입력에서 정수를 읽어서 UF 객체를 생성한다. 그 이후의 표준 입력이 비어있지 않다면, 입력에서 두 정수를 받아서, 두 객체가 연결되어 있지 않다면 둘을 연결시켜서 이를 출력한다. 연결이 되어있다면 무시한다. 이게 우리의 테스트 클라이언트 프로그램이며 이 정도면 우리가 하려는 것을 할 수 있는 적절한 테스트 클라이언트다. 지금까지 구현하는데 필요한 연산에 대해 설명했고 이를 실행하는데 필요한 클라이언트 코드를 살펴보았다.
해당 문서는 다음 링크를 바탕으로 공부한 내용을 정리한 글입니다.
coursera
