Component of Network
- objects : Nodes, Vertices denoted by N
- Interactions : Links, Edges denoted by E
- System : Network, Graph denoted by G(N,E)
Graphs
Common Language
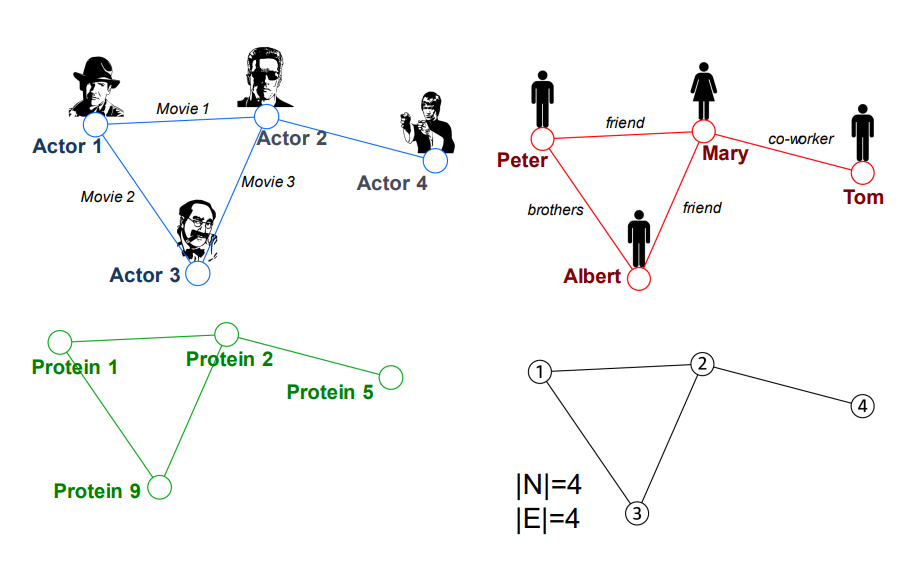
위의 예시는 모두 다른 Domain 이지만 Representation은 동일함
ML의 예측결과가 모두 동일할 것이라는 것
따라서 적절한 Representation을 선택하는 것이 중요
적절한 Link를 찾자
Define
- Choose Nodes
- Choose Edges
- Choise Proper network Representation that determine ability to use networks
Directed vs Undirected
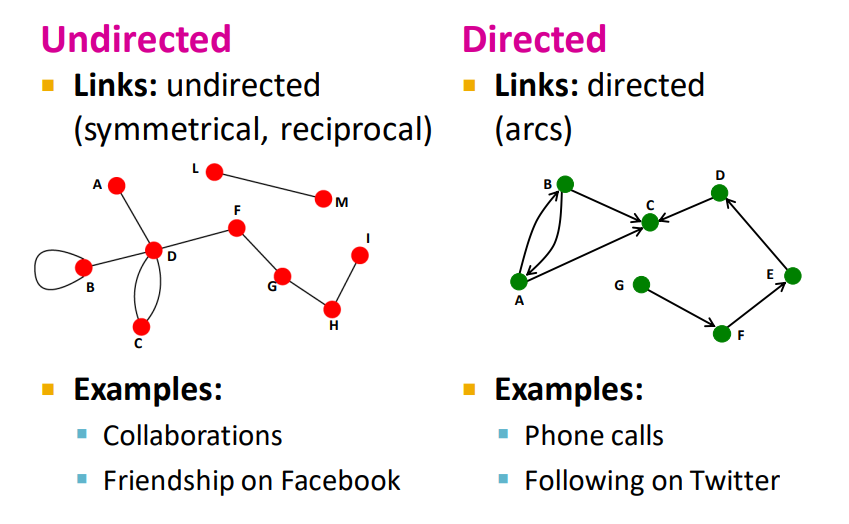
방향이 없는 경우 대칭, 상호관계를 모델링하는데 용이
Node degree
노드에 인접한 Edge의 수
Average Node degree : 모든 노드의 차수의 평균 = 2 * num_Edge / num_Node
왜 2? Edge는 가장자리가 두개니깐
만약 방향이 존재한다면 In-degree와 out-degree로 나누어짐
In degree와 Out degree의 합이 Total degree가 되는 것
Bipartite Graph (이분 네트워크)

노드가 다른 유형의 노드와만 상호작용 하는 Graph
- 저자 - 논문
- 배우 - 영화
- User - Item 등
Multipartite Graph도 존재
Folded/Projected Bipartite Graph
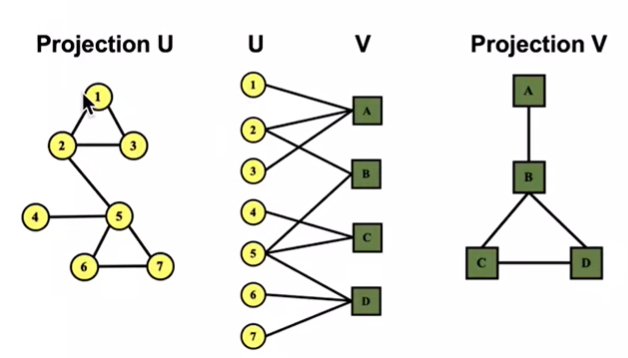
다른 유형의 노드와 연결된 노드로 같은 유형의 노드를 연결하는 것
한 논문에 연결되어 있는 저자들은 교신 저자 이겠지
Representing Graphs
Adjacency Matrix
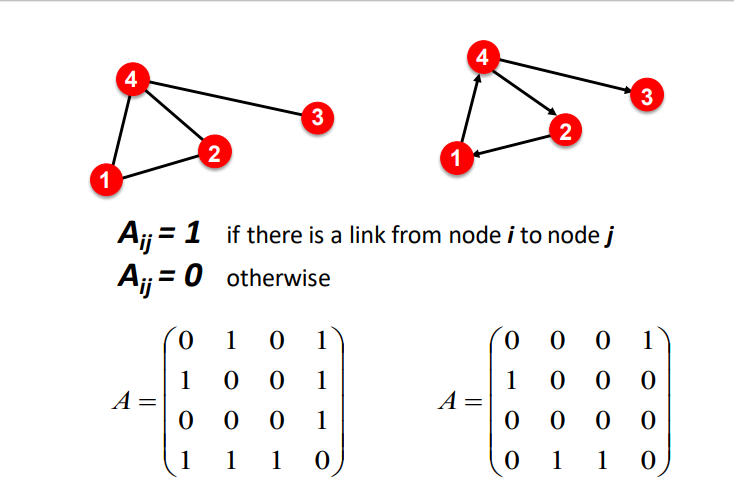
무방향 그래프일 때는 대칭 행렬이며, 방향이 존재할 경우 대칭이 아님
Total Degree 계산은?
무방향 일 경우 1의 총합
방향이 존재할 경우 열별, 행별 1의 총합
Adjacency Matrix의 경우는 매우 Sparse하다는 특징이 존재
전체 노드 개수가 N일때 한 노드의 최대 drgree는 자신을 제외한 모두와 연결되어 있는 N-1임
그러나 대부분의 경우 매우 Sparse한 결과를 낳을 것
Edge List

2차원 리스트로 표현하는 것
조작이 어렵다는 단점
Adjacency list

Sparse 할 때 간단하게 작성할 수 있어 꽤나 유용
Attribute
각 Node, Edge에는 속성이 추가될 수 있음
- Weight
- Rank
- Type
- Sign
Node와 Edge 뿐만 아니라 Side information도 계산해야 한다는 것...
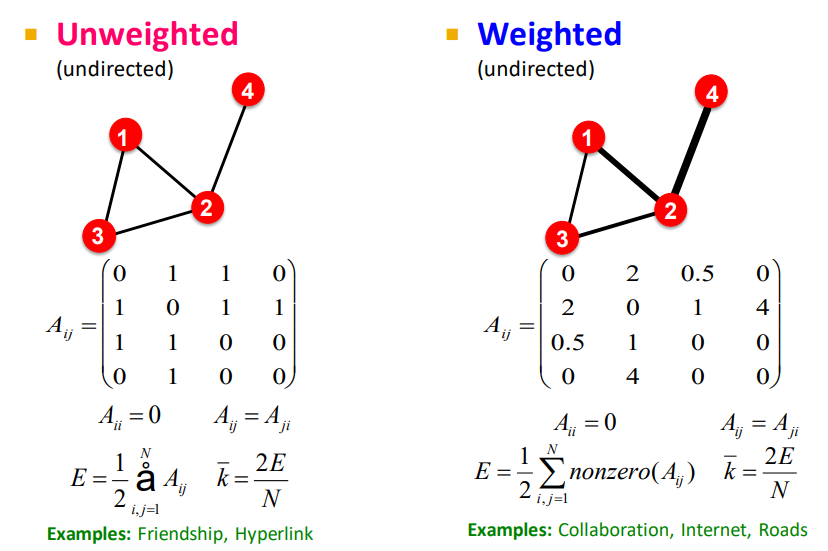
Unweighted 와 Weighted 둘 다 인접 행렬로 나타낼 수 있음
2와 4는 강한 연결을 가지고 있는 걸 볼 수 있음
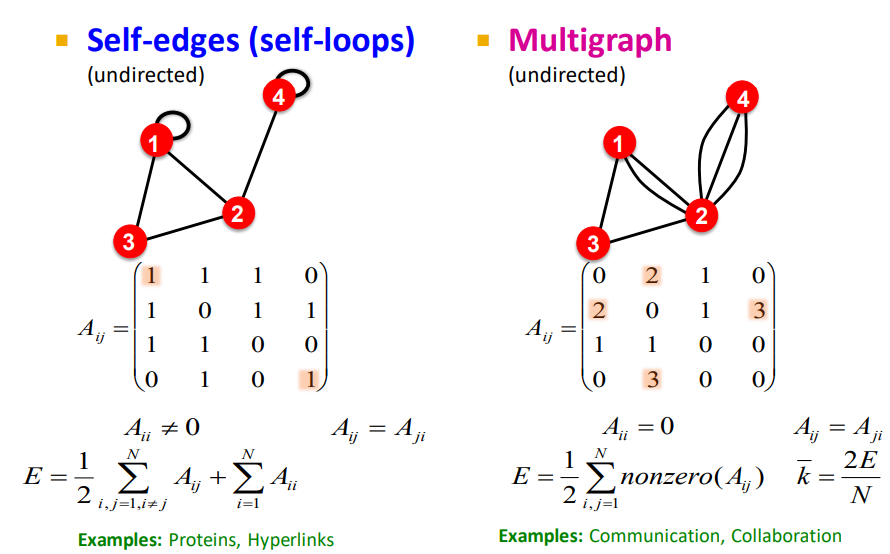
자기 자신에게 연결이 있거나, 중복된 Edge를 가지는 특수한 Graph도 존재함 (둘다 무방향 그래프)
Connectivity
Edge로 연결되어 있을때 Node가 Connect 되어 있다고 할 수 있음
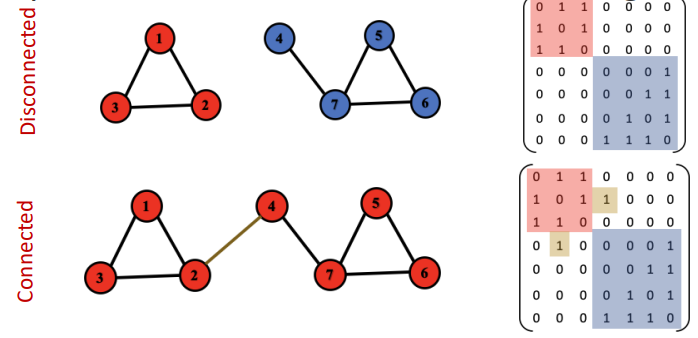
다음과 같이 대각 행렬 영행렬로 나타낼 수 있음
Directed Graph
- Weakly Connect : 한 방향으로만 연결
- Strong Connect : 양 방향 연결
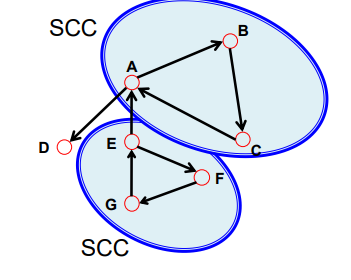
- Strongly Connected component : 양 방향 연결된 Node의 집합

