
Traditional ML PipeLine
- Design for nodes/links/graphs
- We have to attach attribute that help predict network
- Goal is a structure of feature
Train an ML model
- SVM, Random Forest
Feature design
- 전통적인 Feature desing은 Handcraft
- 오늘의 강의는 이러한 수작업의 모든 것을 총 망라
- 단순하게 무방향 그래프에만 초점을 맞춰 알아볼 것
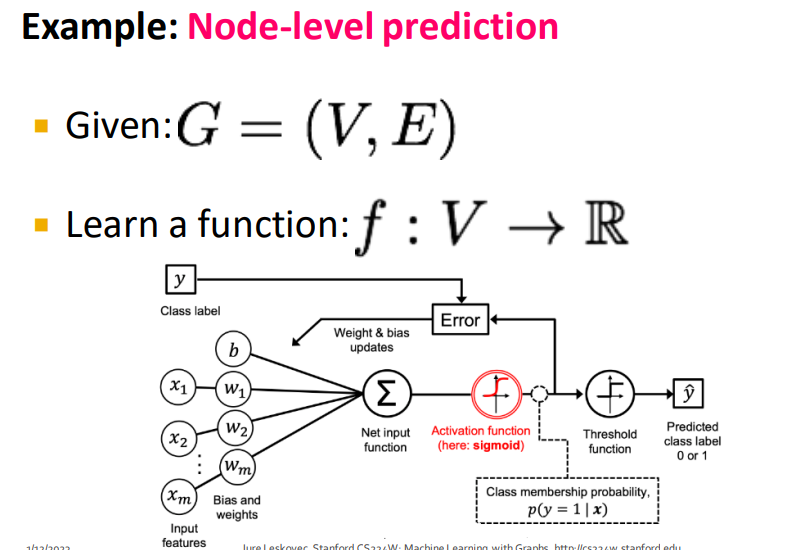
- Goal : predict
- Features : d-demensional vectors
- Objects : Nodes, edges, set of nodes, graph
Node Feature
Node degree
- 노드의 edge 수
- 컴퓨터는 차수가 같으면 모두 동일하게 판단할 것이라는게 단점이라면 단점
Node Centrality
- 이 노드가 그래프에서 얼마나 중요한지
- 여러가지 Centrality를 표현하는 알고리즘이 존재
Eigenvector centrality
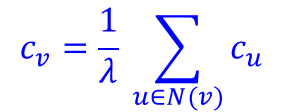
N(v)는 v의 이웃 노드들이며 Cu는 노드 u의 중요도
- 노드의 이웃들이 중요할 수록 그 노드의 중요성이 증가

A는 인접행렬
- eigenvector equation
Betweenness centrality
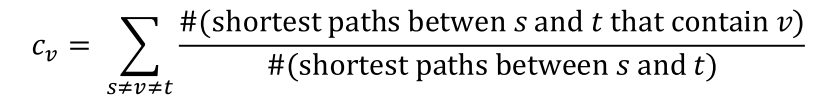
- 노드가 많은 노드 쌍 사이에 있는 경우 중요
Closeness centrality
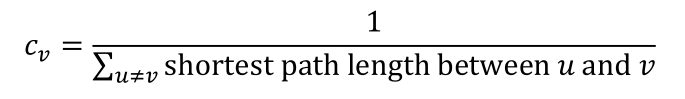
- 다른 모든 노드에 대한 경로가 가장 짧은 경우 중요한 노드
경로가 짧을수록 합계가 작아 중앙에 놓일 것이라는 가정
Clustering Coefficient
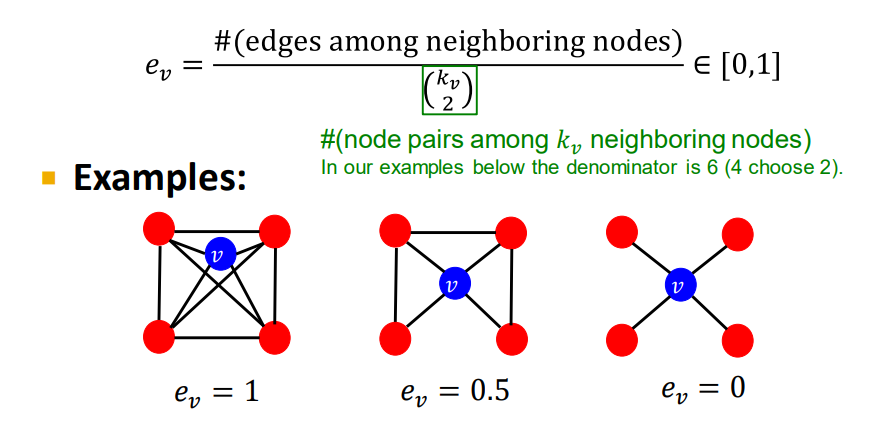
- 지역적인 특성 (클러스터링 계수)
- 이웃과 얼마나 연결되어 있는지
0은 이웃이 모두 연결되있지 않고, 1은 이웃이 모두 친구인 것
Graphlets
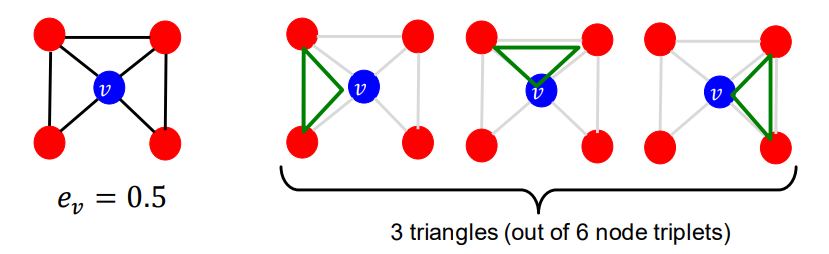
-
클러스터링 계수는 그래프에서 삼각형의 갯수를 세는 것
-
SNS에서 내 친구의 친구는 내 친구일 확률이 있으니, 이 클러스터링 계수는 매우 중요
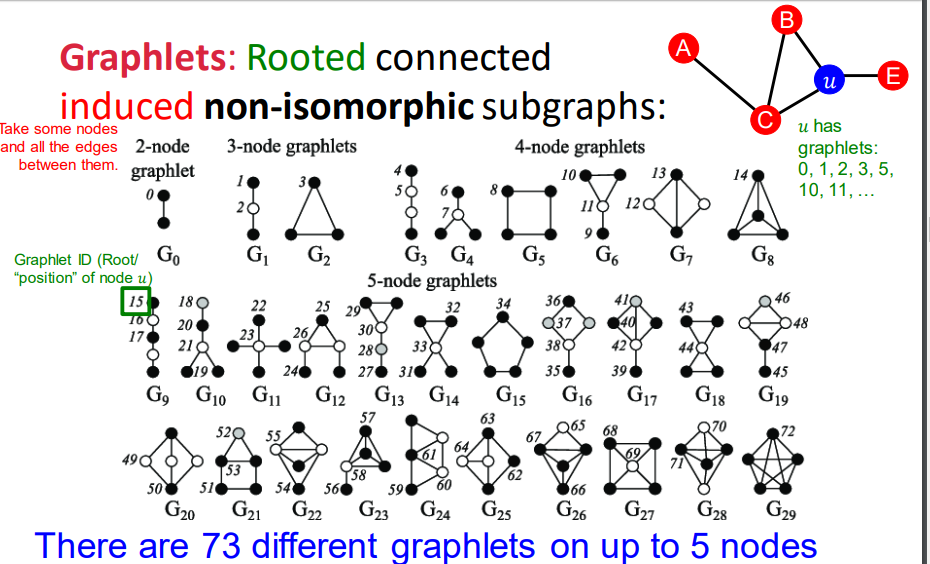
-
헌데 triangle, 3개의 Node는 또 다른 subgraph이기도 함
-
여기서 다양한 모양의 부분 그래프를 추출해보자
-
Graphlet은 뿌리(노드)가 있는 연결된 고정 subgraph
GDV
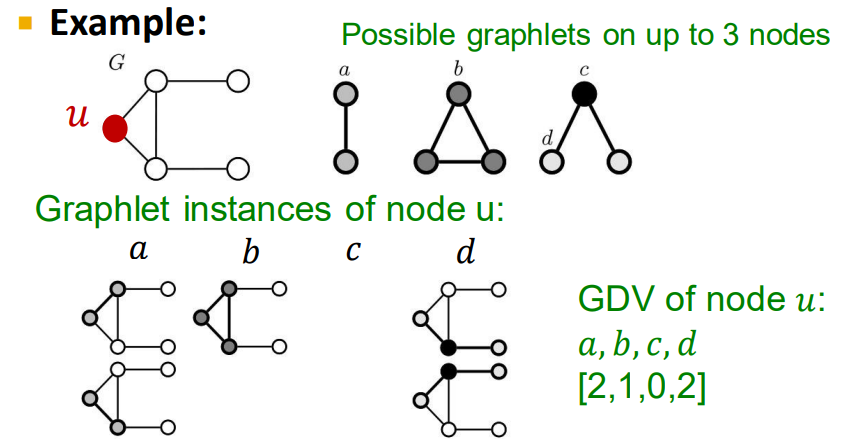
-
Graphlet-base features for nodes
-
v라는 노드가 가지는 GDV 벡터를 다음과 같이 나타낼 수 있음
-
5차수 graphlets 까지 총 73개의 위치가 존재함을 알 수 있음
-
이 한 노드에서 고려해야할 73가지의 73차원벡터를 GDV라고 함
-
모든 4 hops의 거리 까지의 상호작용을 포착
-
노드의 지역적 위상을 가리키는 지표가 바로 GDV 인 것
Summary
종합적으로 Node 수준의 Feature를 살펴 보았으며 중심성, 차수 등 다양한 지표가 존재하는 것을 알 수 있음
