[CS224W] 2.3 Traditional Feature-based Methods: Graph

Graph의 구조를 설명하는 kernel 찾기

Kernel Methods

• Design Kernels instaed of feature vectors

Kernel

• K(G,G')은 유사성 척도
• K는 항상 P.S.D (positive eigenvalues)
• Kernel은 vector 표현의 내적
• 커널이 정의되면 SVM과 같은 Method 사용 가능

Graph Kernel

define graph feature vector pie(G)

• BOW(Bag of words) for a graph
  Node를 단어로 간주, 단어의 횟수를 Count
  Naive하기에, 위치와 edge를 고려할 수 없음..

degree Kernel

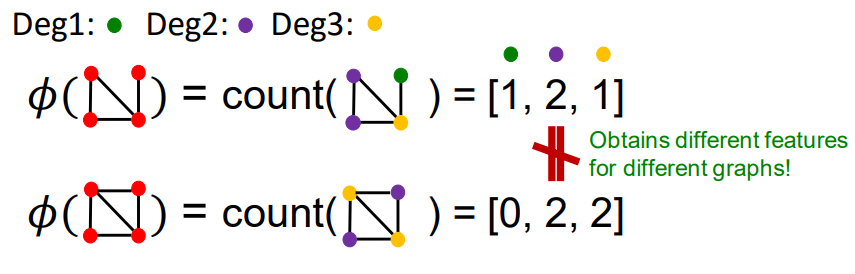
• degree 개수를 기준으로 kernel 생성
  즉 1차 degree 몇개, 2차 degree 몇개.. 요런식

• Graphlet Kernel과 Lemman Kernel 모두 bag of something 의 구조

Graphlet Kernel

• 서로 다른 graphlet의 수를 세는 kernel (Bag of graphlets)

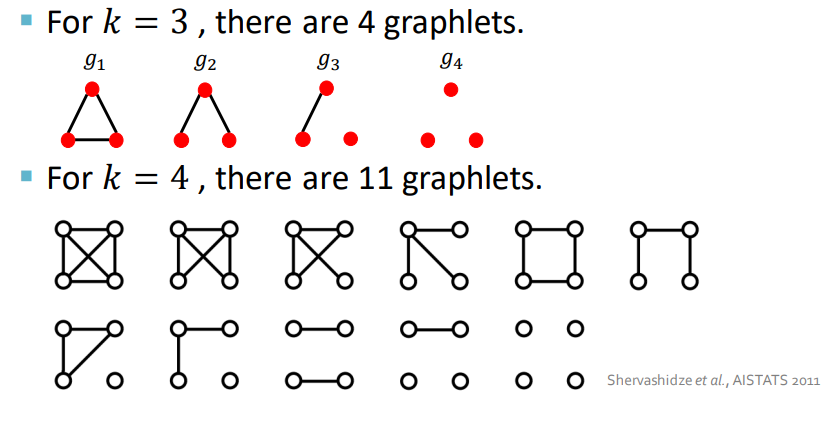
• Link 수준의 graphlet과는 두가지 이유로 다름
  노드들이 무조건 연결될 필요 X
  고정될 필요 X

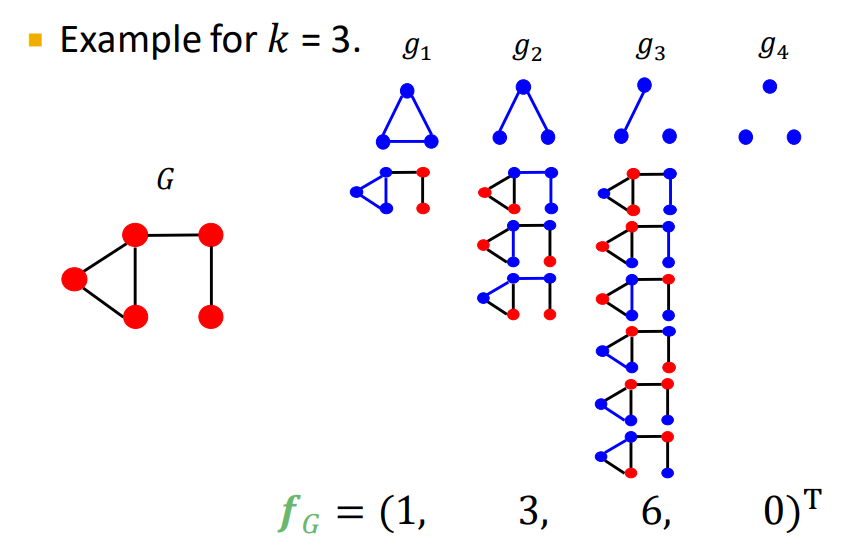
이런식으로 벡터 표현

• graphlet kernel은 다음과 같이 내적의 표현으로 바꿀 수 있으나, G와 G'의 size가 다를 경우 문제 발생
• Normalize해서 해결

Graphlet kernel은 k가 커질수록 지수함수적으로 커지기에 비용이 매우 큼

Weisfeiler-Lehman Kernel

• design an efficient graph feature descriptor pie(G)
• Use neighborhood structure to iteratively enrich node vocab
• Degree kernel이 1-이웃 neighborhood 이므로 이를 확장한 것
• Color Refinement 알고리즘을 통해 구현 (Bag of colors)

Color refinement

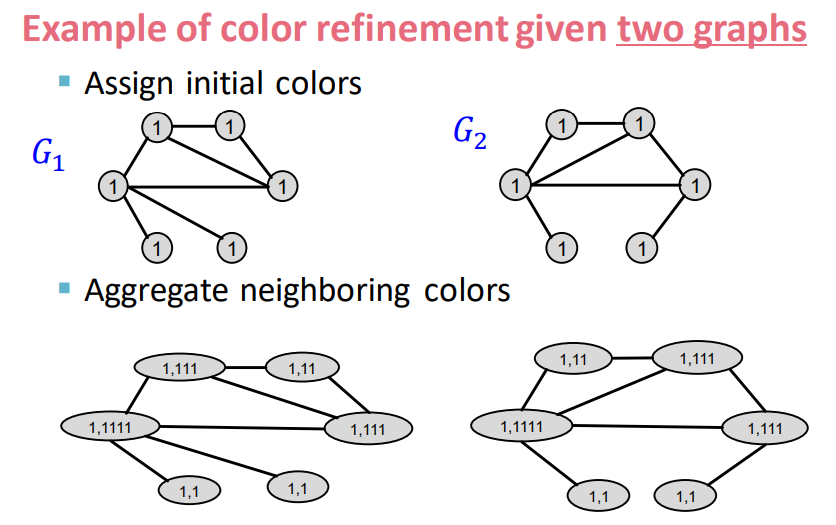
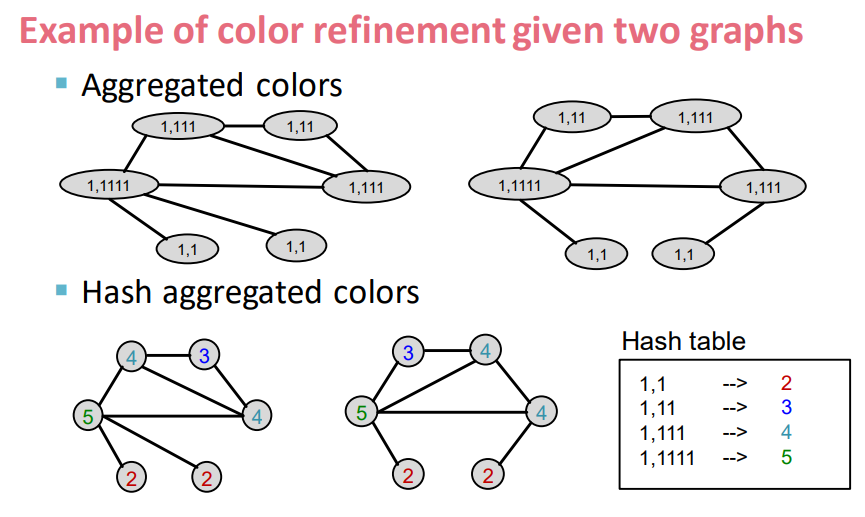
1. 최초 색상 동일하게 배정
2. 인접 노드에 aggregate한 색상을 추가
3. 새로운 aggregation 들을 범주화 해 새로운 색상으로 변경 (Hash Function)
4. 2로 이동 (k번 Iterate)
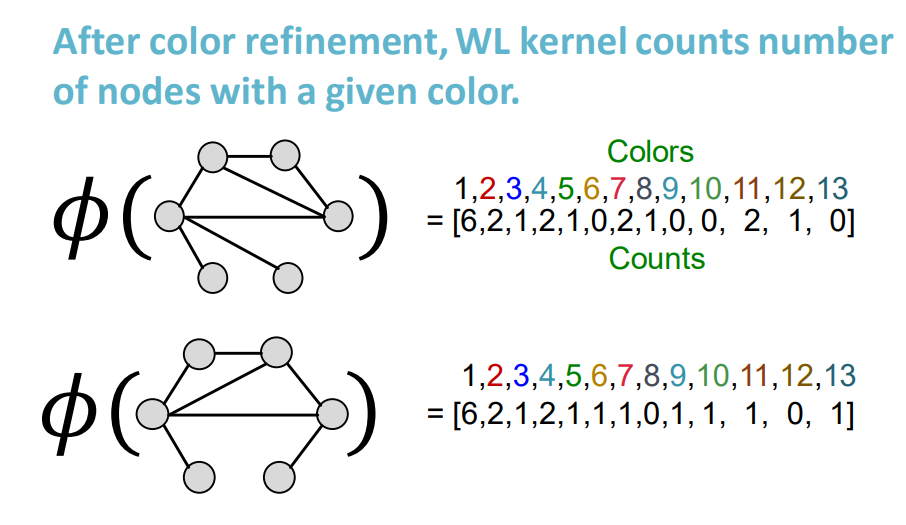
5. k번 반복한 후 주어진 색상이 있는 Node의 수를 계산

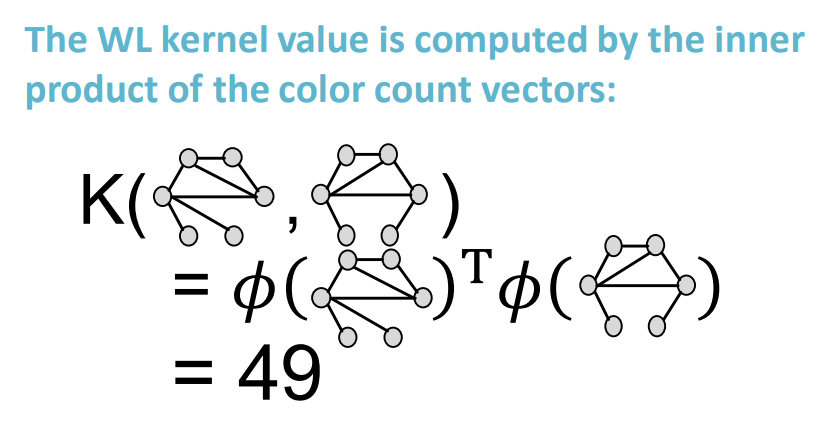
• 내적을 통해 최종적으로 다음과 같은 유사도를 얻을 수 있음

• 매우 강력하고 효율적(시간복잡도가 Edge 개수에 비례한 선형)

• GNN과 밀접한 연관성을 가짐