UltraGCN: Ultra Simplification of Graph Convolutional Networks for Recommendation (CIKM 2021)

Abstract

• GCN의 Core Mechanism은 Message passing
• Message Passing이 과연 꼭 필요한 것인가?
• NGCF를 단순화한 LightGCN으로도 충분치 않다
• LightGCN 보다 더 단순하면서 빠른 동시에 성능도 챙기는 UltraGCN 모델을 제안

Introduction

• 일반적으로 GCN에서 이웃 정보를 aggregate하는 message passing 과정에서 많은 시간이 소요 됨
• LightGCN으로 단순화 하여도, Amazon-Book 데이터셋에서 수렴하는데 까지 700에폭 이상 소요됨
• 우리가 밝혀낸 LightGCN의 한계는 총 3가지 임
  • Message Passing 중 edge에 할당된 가중치는 직관적이지 않아 CF에 적합하지 않을 수 있음
  • 전파 과정에서 User-Item, Item-Item, User-User의 관계를 재귀적으로 학습하여도, 다양한 중요도는 학습하지 못함 + 일종의 노이즈로 작용할 가능성이 있음
  • Over-Smoothing Issue로 인해 모든 embedding이 유사한 값을 가져 성능을 떨어트릴 수 있음
• 따라서 우리는 message passing을 대신해 근사적인 무한한 layer convolution을 찾는 매우 간소화된 GCN 모델인 UltraGCN을 제안함

Notation

Motivation

• GCN과 LightGCN의 한계를 규명하겠음

Revisiting GCN and LightGCN

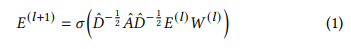
• GCN은 representative model로 message passing을 통해 이웃 정보를 aggregate 함

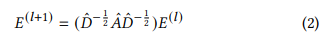
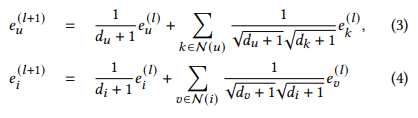
• LightGCN은 nonlinear activation과 feature transform term을 제거해 GCN을 간소화하였고, 성능 향상과 효율성을 획득함

Limitations of Message Passing

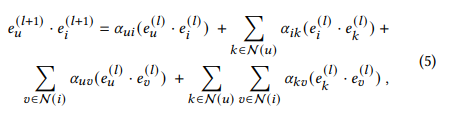
• u와 v가 user이고, i와 k가 item일 때, 선호도인 dot product는 다음과 같은 식으로 정리 됨

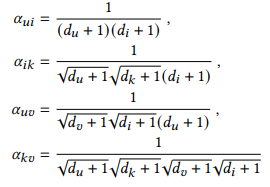
• 이때 signal들은 다음과 같이 표현 가능하며, user와 item relationships(u-i, k-u), item과 item relationships(k-i), user와 user relationships(u-v)로 표현 됨

• 그러나 이러한 signal은 경험적으로 3가지 한계를 가짐

  • item간의 signal인 aik는 비대칭임 (k의 차수는 root) 따라서 item k와 i를 동등하게 보지 않기에 합리적이지 않음
    
  • 경험적으로 message passing을 쌓는 것은 성능이 좋지 않고 효율적이지 않음 (노이즈가 포함 됨)
  • High order signal을 찾기 위해 Layer를 쌓다 보면 Over smoothing 문제가 발생 함
    

• 상기된 이유로 우리는 message passing이 실질적인 의미가 있는지 의문을 가짐

UltraGCN

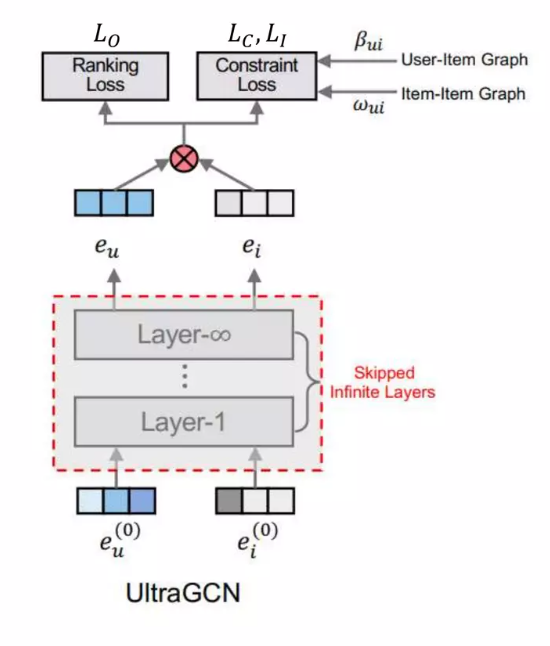
Learning on User-Item Graph

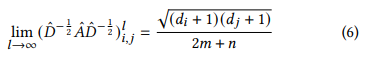
• Message passing이 극한으로 가면 다음과 같이 공식화 됨

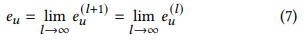
• 만약 message passing layer를 무한으로 쌓았다면 다음과 같은 공식을 따르게 됨 이것을 equation 3에 적용한다면...

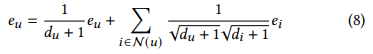
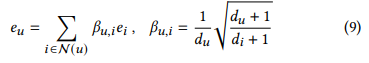
• 다음과 같은 식이 나옴
• 각 노드가 equation 9에 만족한다면, 단번에 message passing의 수렴 상태에 도달할 수 있음

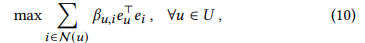
• 이 수렴을 학습하기 위해서는 다음 식을 최적화해야 함 (코사인 유사도를 극대화 하는 식)

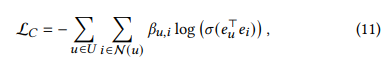
• 식을 간단하게 하기 위해 시그모이드와 로그함수를 첨가하고, 다음과 같은 loss function이 등장
• 이 Loss를 우리는 constraint loss라고 부르고 bu,i를 constraint coefficient라고 부르겠음

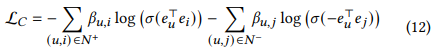
• 다만 constraint coefficient를 요구하는 제약식 때문에, 모든 Interaction을 요구하게 되고, 자연스레 over smoothing issue가 발생함
• GCN과 LightGCN은 Layer 수를 조절하는 것으로 문제를 해결하였지만, UltraGCN은 무한히 수렴한 것을 가정하므로, negative sampling을 통해 이를 해결 함
• 상기된 수식이 최종적인 constraint loss이며, 즉시 무한히 message passing을 진행한 효과와 over smoothing을 피하는 효과를 얻을 수 있음

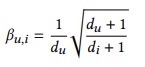
• constraint coefficient는 제약식의 loss weight 역할을 하게 되는데, 이는 du와 di를 작게한 값으로, interaction이 많은 item, user에게는 작은 loss weight를 주는 것으로 설명할 수 있음

Optimization

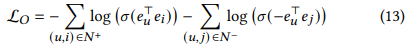
• 전형적으로, CF 모델에서는 pairwise loss인 BPR loss와 pointwise loss인 BCE(Binary cross-entropy) loss 둘 다 사용됨
• 우리는 CF를 link prediction 문제로 graph learning에 사용하고 있기에, BCE loss를 main optimization으로 채택하며, 제약식과 동일함

• hyperparameter lambda와 함께, 새로운 제약식과 기존 제약식을 적절히 섞어서 사용함

Learning on Item-Item Graph

• Equation 5와 같이, GCN 모델은 Item-Item, User-User Interaction을 포착할 수 있음
• 다만 전통적인 GCN 모델에서 이러한 Interaction의 실효성은 검증되지 못함
• 우리의 모델 UltraGCN은 더 Flexible -> 새로 Item-Item matrix, User-User matrix, 심지어 Knowledge Graph를 만들어 사용 가능!

• 한 예시로 item co-occuruence matrix를 사용할 것

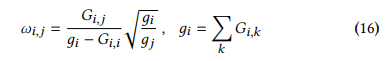
• 동일하게 equation 9 처럼 공식화 가능하며, gj는 degree에 해당
• equation 12와 유사한 constraint loss가 생성되고, constraint coeifficient는 wij
• 다만 co-occurrence matrix는 기존 user-item matrix처럼 sparse하지 않지 않은 dense matrix 이기에, 이전 GCN 계열 모델에서 설명한 Limitation 2와 같은 현상이 발생할 가능성이 높음

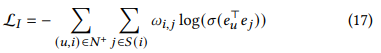
• UltraGCN은 유연하게 대응 가능, 모든 정보가 아닌 유용한 정보만 사용하면 됨
• 직관적으로, wij는 일종의 유사도 척도 임을 알 수 있음
• 따라서 wij가 높은 i에 대한 top K개의 j 아이템을 추출하고, over smoothing에 대한 대비는 충분히 되었기에 이번에는 negative sampling을 사용하지 않음

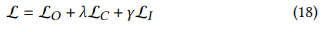
• 총 제약식을 다음과 같이 정의할 수 있음 (람다와 감마는 Hyperparameter)

Discussion

• 우리의 edge weight인 bij와 wij는 더 합리적이고 해석가능 함
• 직접적인 message passing 없이, 더 유연하게 데이터를 사용할 수 있음
• UltraGCN이 다양한 제약식을 만족시키는 multi-task learning 이지만, 모두 유사한 형태의 BCE이기에 빠르게 수렴 가능함
• 감마를 조절하여 user-item graph만 사용할 지 등, 유연하게 학습 가능
• 다만 최근 모델에서는 user-user graph는 학습에 사용하지 않음 (user의 취향은 너무 broad하여 학습이 잘 되지 않음) 전통적인 GCN 모델은 user-item graph를 통해 모든 interaction을 학습하려 하는데, 여기서 limitation 2가 발생하는 것으로 추정
• 이를 해결하기 위해 social network graph를 사용하는 등 추후 과제로 남겨둠

Relation to MF

• UltraGCN은 가중치가 적용된 MF 모델로, CF에 맞게 조정된 BCE Loss를 사용함
• 다만 이전 MF 모델과 달리 UltraGCN은 그래프를 사용하여 빠르고 깊게 정보를 얻음

Relation to Network Embedding Methods

• DeepWalk, LINE, Node2Vec과 같은 negative sampling을 이용한 node embedding 방법론과 유사하다고 할 수 있음
• 다만, UltraGCN은 더 합리적이고 의미있는 edge weight를 가진다는 점에서 다름
• 실험적으로도, UltraGCN이 더 우수함

Relation to One-Layer LightGCN

• LightGCN은 embedding aggregation을 위해 weight combination을 채택한 반면, UltraGCN은 constraint coefficients가 constraint loss function에 부여 됨
• 이는 layer graph convolution을 무한히 통과하였을 때를 가정
• 특히 실험적으로, UltraGCN이 LightGCN의 한계를 극복하였음

Complexity

• b와 w는 미리 구할 수 있으므로 O(1)
• training time은 O(num(top k) + num(negative samples) + 1) num(user item interactions) ((embedding dimension)^2 + 1)
• k를 작게 지정한다면, MF의 시간 복잡도인 O((R + 1) num(user item interactions) (embedding dimension)^2) 와 거의 동일
• 별개로, 학습 가능한 파라미터는 오직 item, user embedding 이기에, MF와 LightGCN과 동일

참고한 블로그