
Abstract
- semi-supervised approch on graph structure
- 이는 Spectral graph convolustion의 1차 근사에 해당
- Num of graph edge 따라 선형 복잡도를 가지며, Local Graph와 Node의 Feature를 잘 표현하는 Hidden Layer를 학습
- 다양한 실험 결과를 통해 우리의 모델이 우수함을 보여줌
Introduction
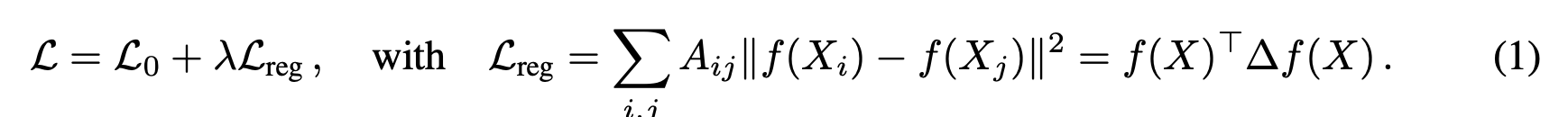
- Node Classifying에서 문제점
- Label 정보가 Smoothing 됨
- Graph Laplacian은 인접한 노드는 같은 Label을 공유한다고 가정
- 그래프의 Edge가 반드시 유사도를 의미하는 것은 아니기에, 이 가정은 추가적인 정보를 함유하는데 한계가 있음
- 따라서 우리는 위 수식의 Laplacian term을 피하고, neural network를 통해 L0 term을 최적화 할 것
- 우리의 공헌도는 두 가지
- Graph representation을 잘 학습할 수 있는 간단한 propagation rule을 도입 (이는 spectral graph convolution의 1차 근사에 해당)
- 이 graph-based neural network model이 빠르고, 확장 가능한 semi-supervised classfication임을 입증 (다양한 실험을 통해 SOTA임을 입증)
Fast Approximate Convolutions On Graphs
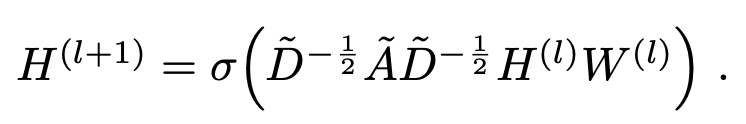
- 우리가 소개할 graph-based neural network의 수식적 이해
- 다층 그래프 컨볼루션 신경망
- A~는 Self-Connection을 추가한 인접행렬
- D~는 Degree 행렬
- W(l)은 weight matrix
- 위 수식이 spectral filters on graphs의 1차 근사임을 증명할 것
Spectral Graph Convolutions
- Spectral Graph Convolution에 대한 간단한 이해
Spatial vs Spectral
- 우리가 원래 아는 CNN은 Spatial Graph Convolution
- filter는 고정된 size
- local invariance (입력의 위치가 바뀌어도 출력이 동일해야 함)
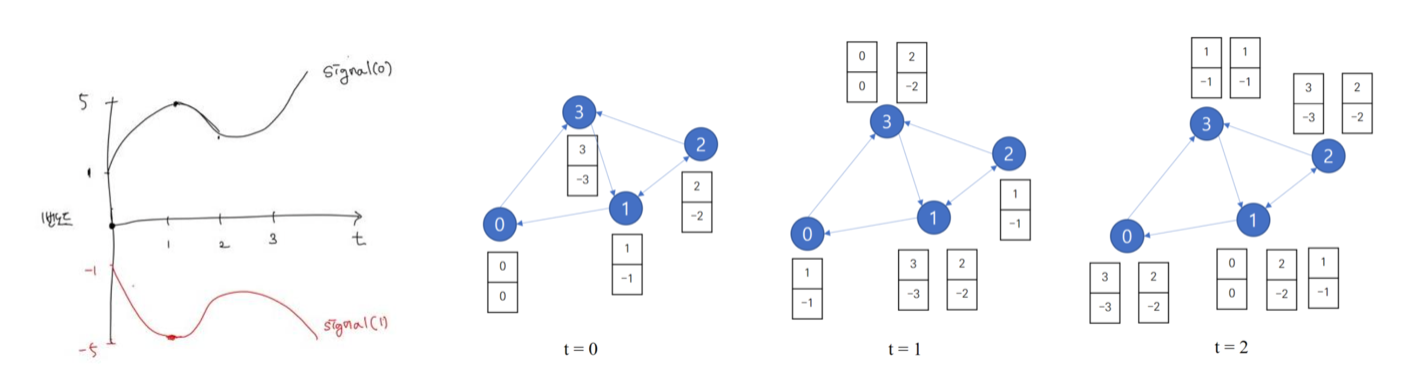
- 반면 graph는 signal이 들어올때마다 node의 정보가 바뀜 (message passing)
- 즉 한 노드의 정보는 여러 노드의 signal이 혼재해 있는 것
Dive into Spectral Graph Convolution
- Signal Processing에서 spectral analysis는 이미지/음성/그래프를 time/spatial domain이 아닌 frequency domain으로 바꾸어 분석을 진행하는 것
- 특정 신호를 단순한 요소의 합으로 분해하는 것 (푸리에 변환)
- 푸리에 변환은 임의의 입력 신호를 다양한 주파수를 갖는 주기함수의 합으로 분해하여 표현하는 것
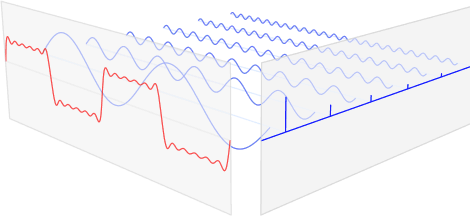
파란색 주기함수의 합이 빨간색 신호가 되는 것
푸리에 변환
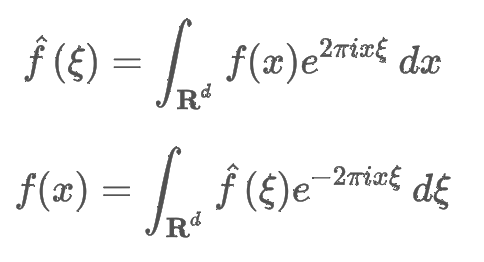
- 식 1은 푸리에 변환, 식 2는 푸리에 역변환
- 푸리에 변환을 바라보는 여러가지 관점 중 하나는 내적 (유사도)
- 임의의 주파수 f(x)에 대해 얼마나 e^식이 얼마나 닮았는지를 보여주는 푸리에 변환 식
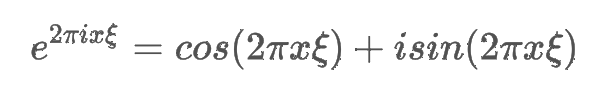
- 오일러 공식을 통해 e^식이 f(x)에 대해 cosine 유사도와 sine 유사도의 합임을 알 수 있음
- 삼각함수의 내적 (sine to sine, cosine to cosine, sine to cosine)은 0
- 이는 선형대수 관점에서 sine과 cosine 기저들의 선형 결합이 푸리에 변환이 되는 것
- 즉 어떤 특정 graph signal에 관한 행렬이 존재하고, 이 행렬이 real-symmetric matrix이며, 이들의 eigenvector를 구할 수 있다면!
- eigenvector의 선형 결합이 graph signal의 푸리에 변환이라는 것
Graph Laplacian
- graph signal에서 laplacian은 한 노드에서의 흩어짐 정도, 흐르는 정도임
- 특정 node signal이 들어왔을 때 얼마나 빠르게 흩어지는지 이며, 이는 곧 노드의 특징이 되는 것
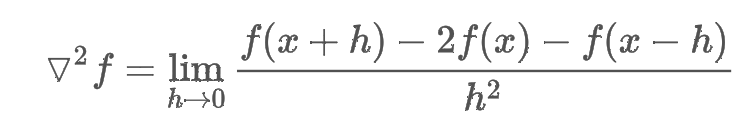
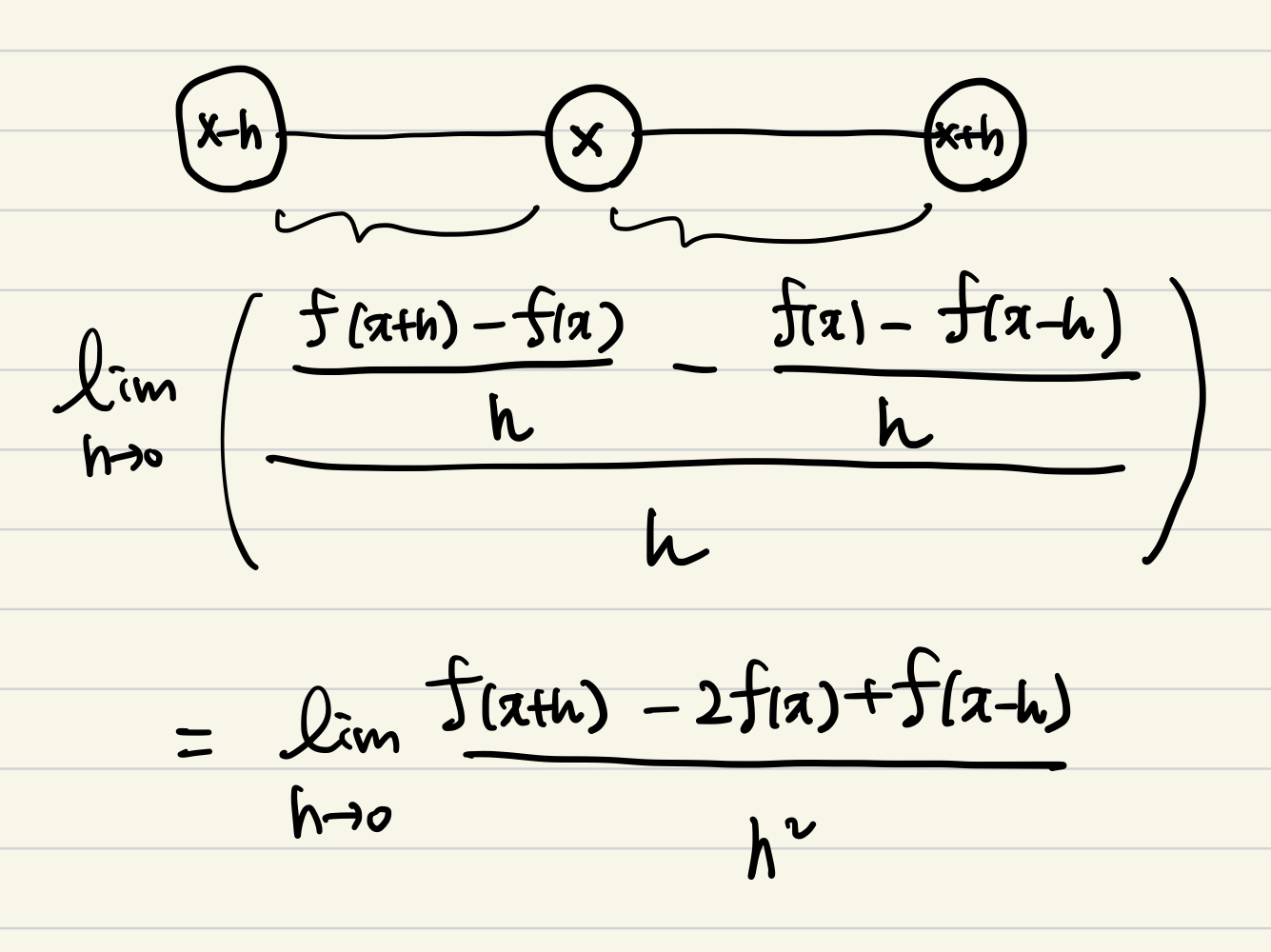
- x 노드의 signal f(x)와 h 만큼 떨어진 이웃 노드의 signal 변화량을 통해 x 노드의 signal 특징을 구한 것
- 이웃 노드와의 차이는 매끄러움(smoothness)를 의미
- 한 노드가 이웃 노드와 차이가 적으면 이웃 노드와 비슷한 것이고
- 차이가 크면 특성이 상이하다는 것 (매끄럽지 않음)
- 이는 신호의 관점에서 한 노드의 신호는 유사한 특성의 노드 신호와 상이한 특성의 노드 신호의 결합으로 표현할 수 있음
Spectral Graph Convolution
- 입출력이 존재할 때, 출력은 이전의 입력값에도 영향을 받음
- 이전 값의 영향을 고려하여 시스템의 출력을 계산하기 위한 연산이 바로 convolution
- 이 convolution의 특징은 시스템의 출력으로 시스템의 특성을 알 수 있다는 것
- 이 개념이 바로 CNN의 filter에 해당
- Graph Convolution은 graph의 특징을 추출해 낼 수 있는 filter를 학습으로 얻고자 하는 것
convolution theorem
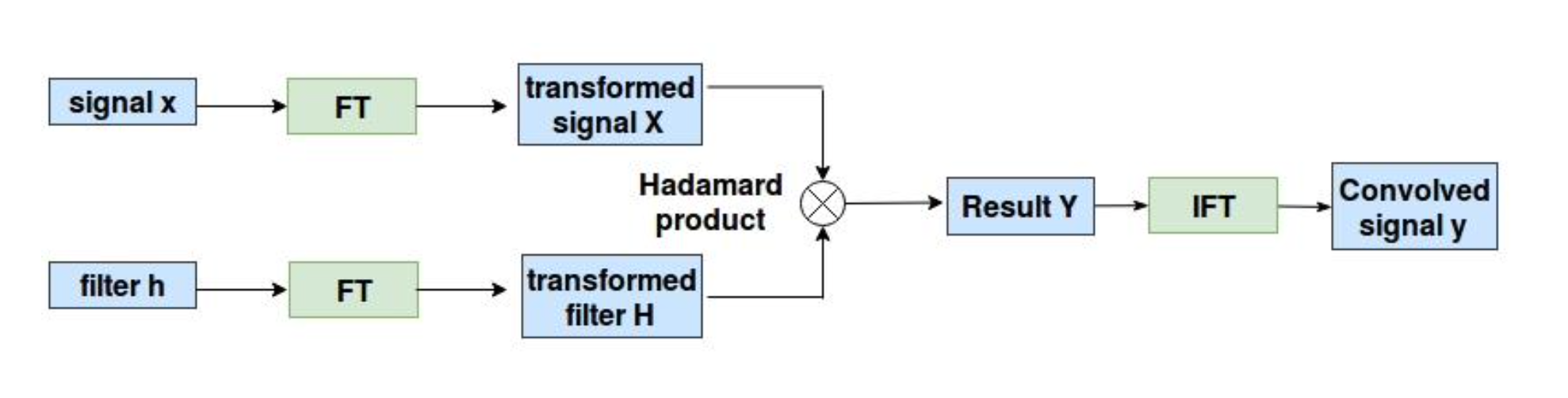
Time 영역에서의 signal과 시스템 함수와의 convolution 연산은 각 frequency 영역 변환 후의 곱과 같다
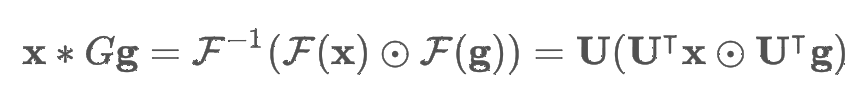
- 학습 filter는 g
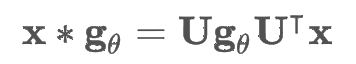
-
만약 g가 대각행렬일 때의 수식
-
다시 돌아와, 이 식에서 U Ut는 복잡도 N^2을 가지게 되고, 더 나아가 eigen value decomposition도 그래프가 커지면 상당한 자원을 소모
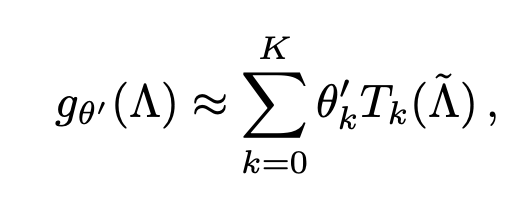
-
이 때 체비셰프 다항식에 따라서 K까지 truncated
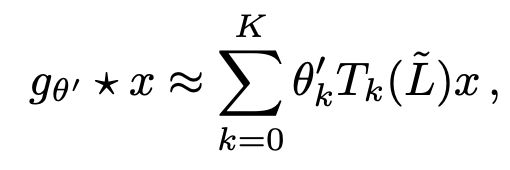
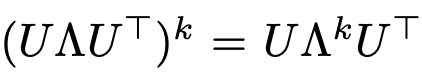
-
다음 식이 완성됨
-
이때 K까지의 neighbor를 고려한다고 할 수 있음
-
복잡도는 edge의 개수에 선형 복잡도를 가짐
Layer-Wise Linear Model
- 여기서 GCN은 K=1로 가정
- 수식은 최종적으로 다음과 같음
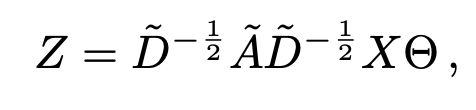
Semi-Supervised Node Classification
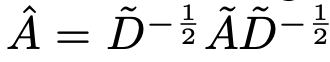
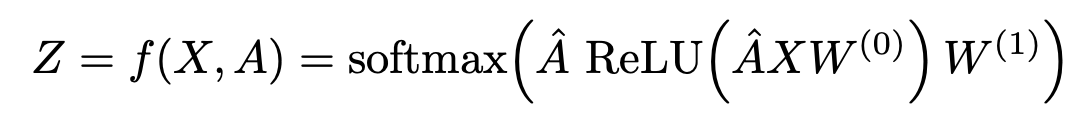
-
앞서 말했듯, 함수에 인접 행렬을 conditioning 해주는 작업으로 여러 가정을 완화함
-
A를 degree matrix로 정규화 하여 우리에게 익숙한 neural network 수식으로 변환
-
softmax를 취해 최종으로 label predict
-
본 논문에서는 full batch gradient descent, dropout을 통해 학습
-
이후 실험 및 관련 연구 서술
