Attention is All You Need - 이해+
Position Encoding
- sequence의 토큰들을 (recurrent하게가 아닌) parallel하게 한 번에 처리한다.
- 즉, 어순 정보를 반영할 time-step 개념이 없어졌으므로, 모델에 어순 정보를 전달해줘야 한다.
- 단어 토큰들에 위치(어순) 정보를 추가로 부여해야 한다.
rule
- 학습하기 위해 positional encoding의 신경써야 할 사항
- input sequence의 값이나 길이에 관계없이, 같은 위치에 대해 같은 값이 유지되어야 한다.
- sequence의 길이가 길어지더라도 연산에 문제없이 위치 정보가 반영 될 수 있어야 한다.
여러 방안과 문제점
- 절대적 위치 정보를 이용한 positional encoding
- 첫 번째 토큰에 1, 두 번째 토큰에 2 … 위치 index에 비례하게 정수 값을 부여
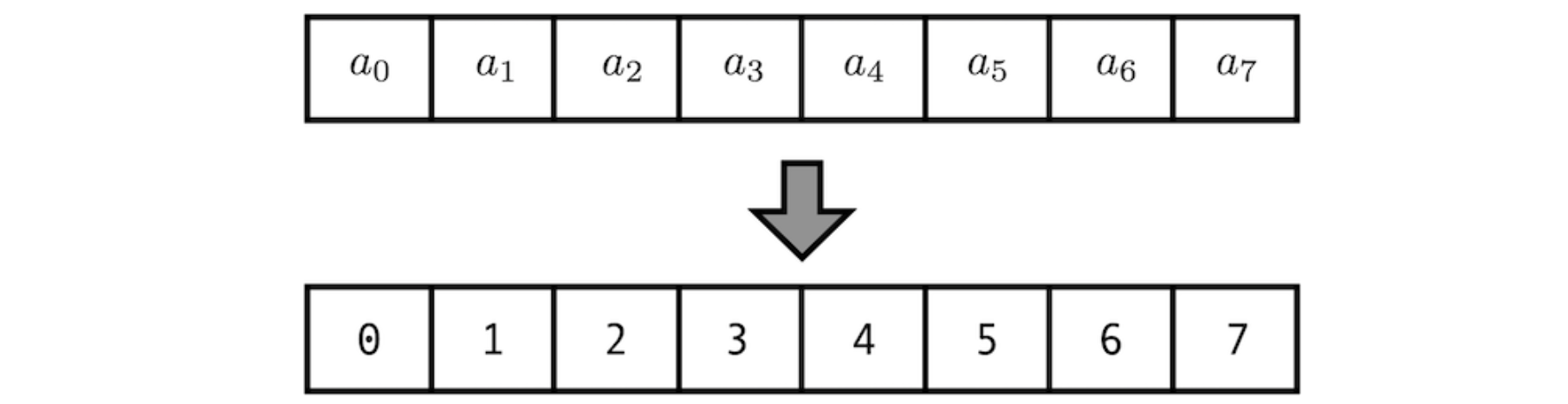
- sequence의 길이가 길어지면 positional encoding 값이 계속 커져서 위치 정보의 영향력이 너무 강해진다.
: 단어의 의미 정보가 묻혀버린다.
- 절대적 위치 정보를 normalization 후 반영
- 값 자체가 너무 커지는데서 오는 문제는 해결.
- 하지만 sequence의 길이가 달라지면 어떤 위치에 대한 positional encoding 값이 달라져버린다.
- 값 사이의 간격 또한 달라진다.
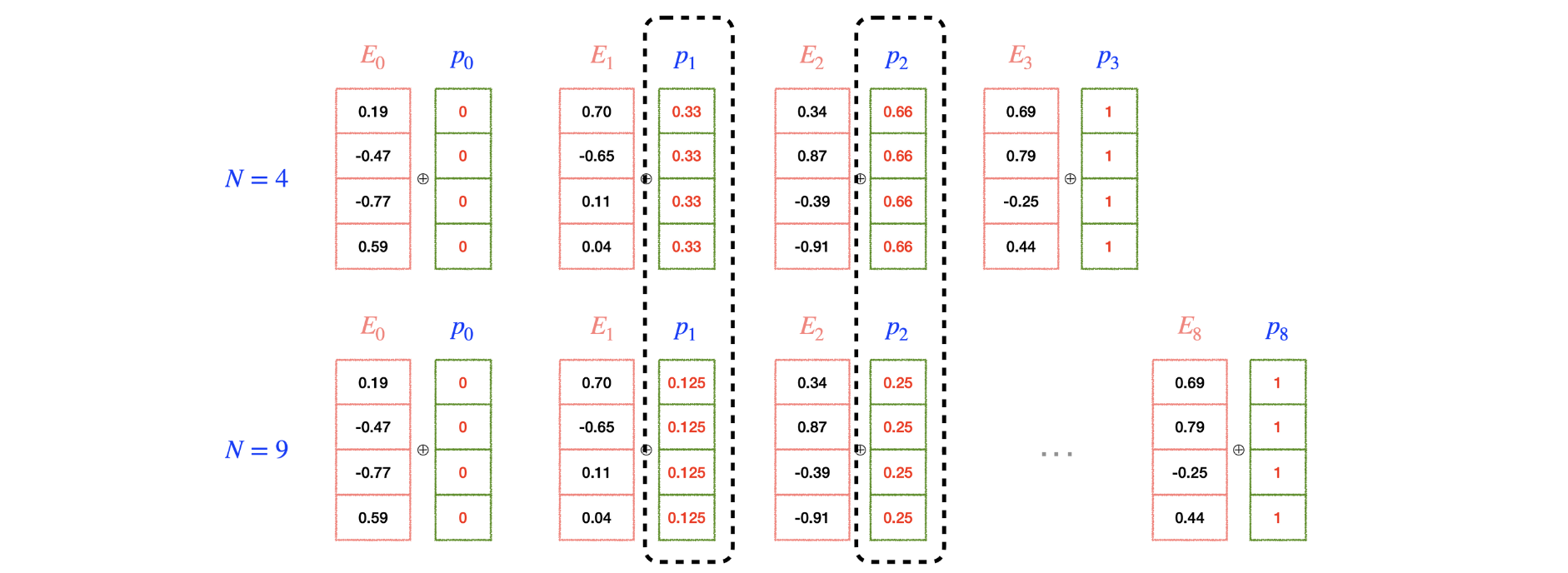
sin, cos 을 이용한 positional encoding
- 다른 주기를 갖는 d(dim=model dimension)개의 sin, cos 함수를 이용한 positional encoding vector를 통해 위치정보를 표현한다.
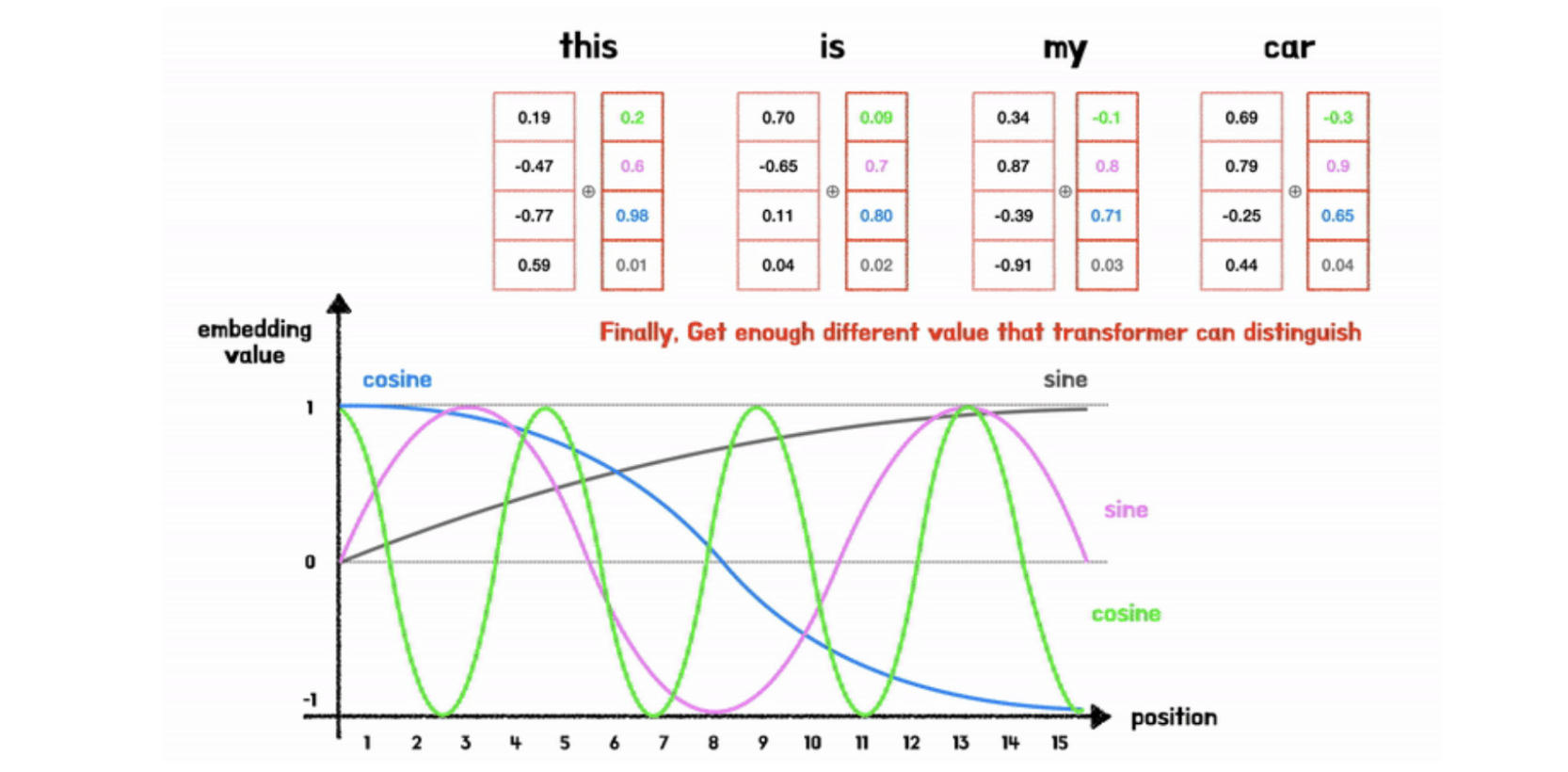
- -1 ~ 1 범위의 값을 가지기에 값이 너무 커지는 문제 발생하지 않는다.
- 같은 위치에 대해 항상 같은 positional encoding vector 값이 유지된다.
- 반복되는 주기 함수이기 때문에 sequence가 길어져도 값 사이에 간격이 너무 작아지지 않는다.
(sigmoid에서 나타나는 문제)
- 반복되는 함수이기 때문에 다른 위치에 대해 같은 값을 가질 수 있는 문제는
→ d개의(차원) 다른 주기 함수로 positional encoding vector를 구성 구성함으로써 해결했다.
: 결국 언젠가는 같은 벡터 값이 나타나겠지만 그 경우의 수를 크게 줄었기에 그 전에 대부분의 위치 정보를 표현 할 수 있다.
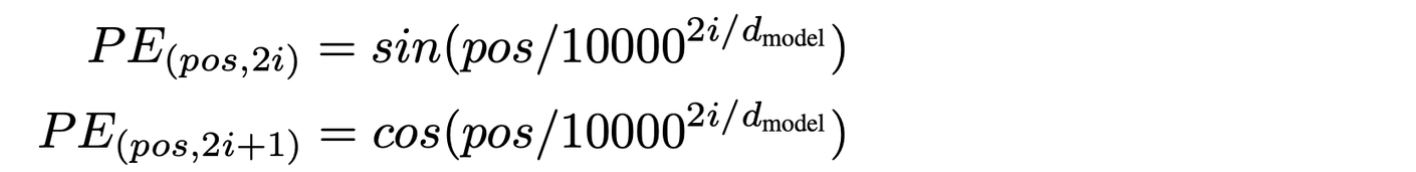
- dim마다 sin, cos 함수를 번갈아서 설정함으로써 벡터 값들 간에 차이를 크게 만든다.
- dim이 커질 수록 sin, cos 함수의 f(진동수)를 키워서 (주기를 짧게 하여) 값 사이에 차이를 만든다.
word embedding 과 position embedding의 정보 결합
- Concatenation
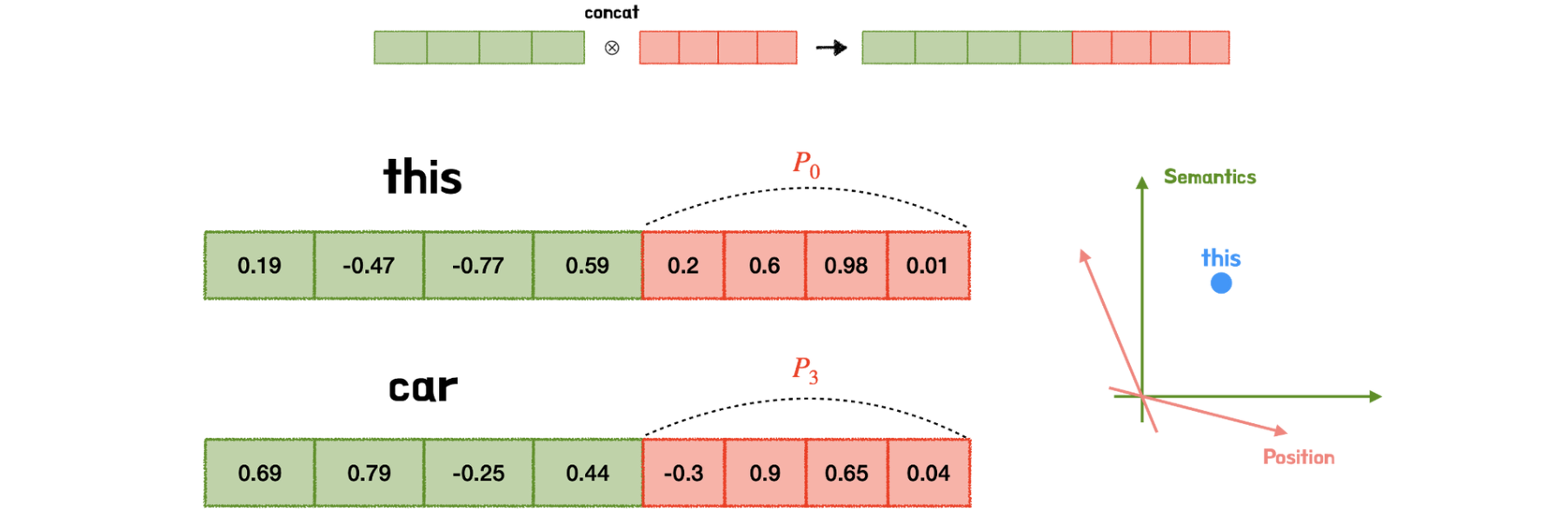
- 두 embedding 벡터가 각각의 차원공간에 위치하게 된다.
- 두 정보가 섞이지 않는 장점이 있다.
- 하지만, 메모리/연산 등 cost가 너무 커지게 된다.
- Summation
- 정보가 뒤섞인다.
- 하지만, 단어 의미 정보가 충분히 보존되고 적절히 위치정보도 반영된다.
- 연산 환경에 충분한 여유가 있다면 concatenation을 사용해도 좋다.
Residual Connection
- 최적화의 난이도를 낮춘다.
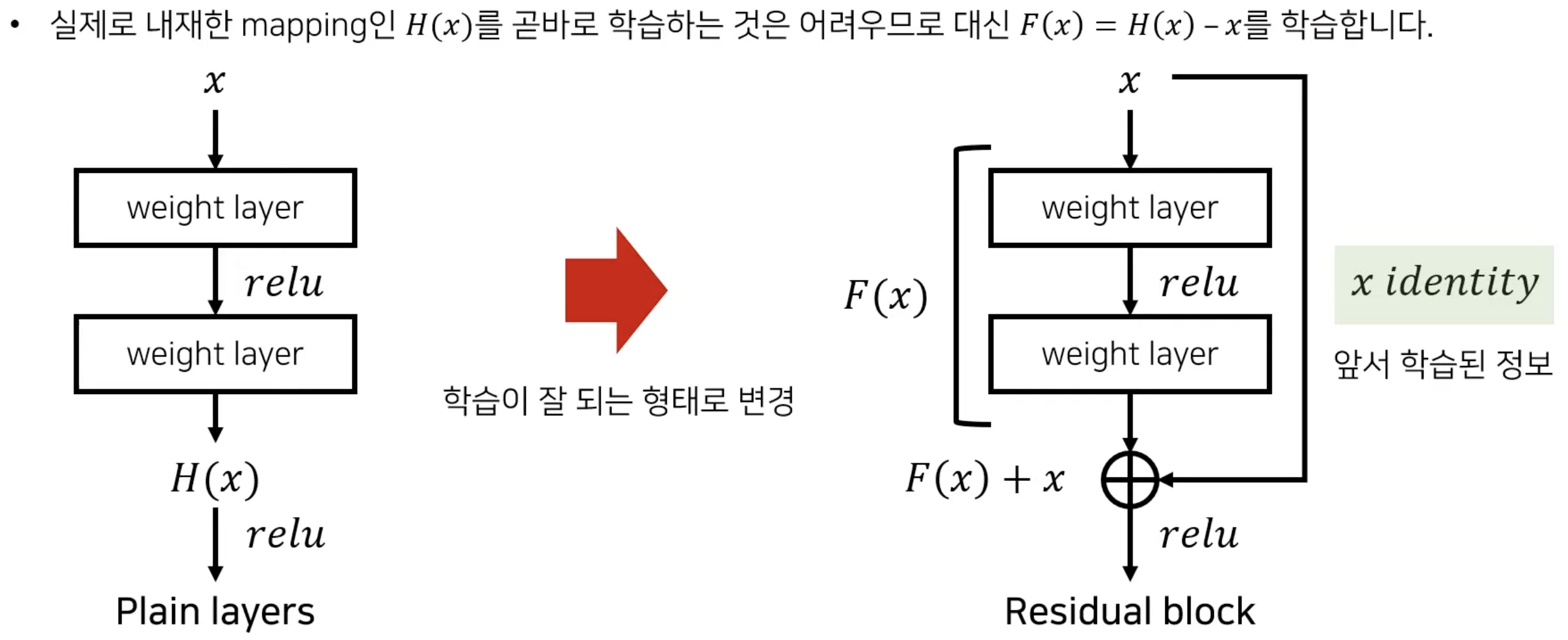

- 상위 layer의 gradient 값이 변하지 않고 그대로 하위 layer에 전달
- vanishing gradient 문제를 완화
흐름에 따른 Token Vector의 dim(shape) 변화
- max_len
: 하나의 sequence data를 표현하는(구성하는) 토큰의 개수
: 모든 sequence 길이는 max_len으로 통일된다. (by. pooling / truncating)
- vocab_size
: tokenizer가 갖고 있는 vacabulary의 size (단어 종류 가짓수)
- emb_dim = model_dim
: word embedding의 표현 vector space 차원 크기
: 하나의 토큰을 embedding 후 몇 차원 벡터로 표현 할지..
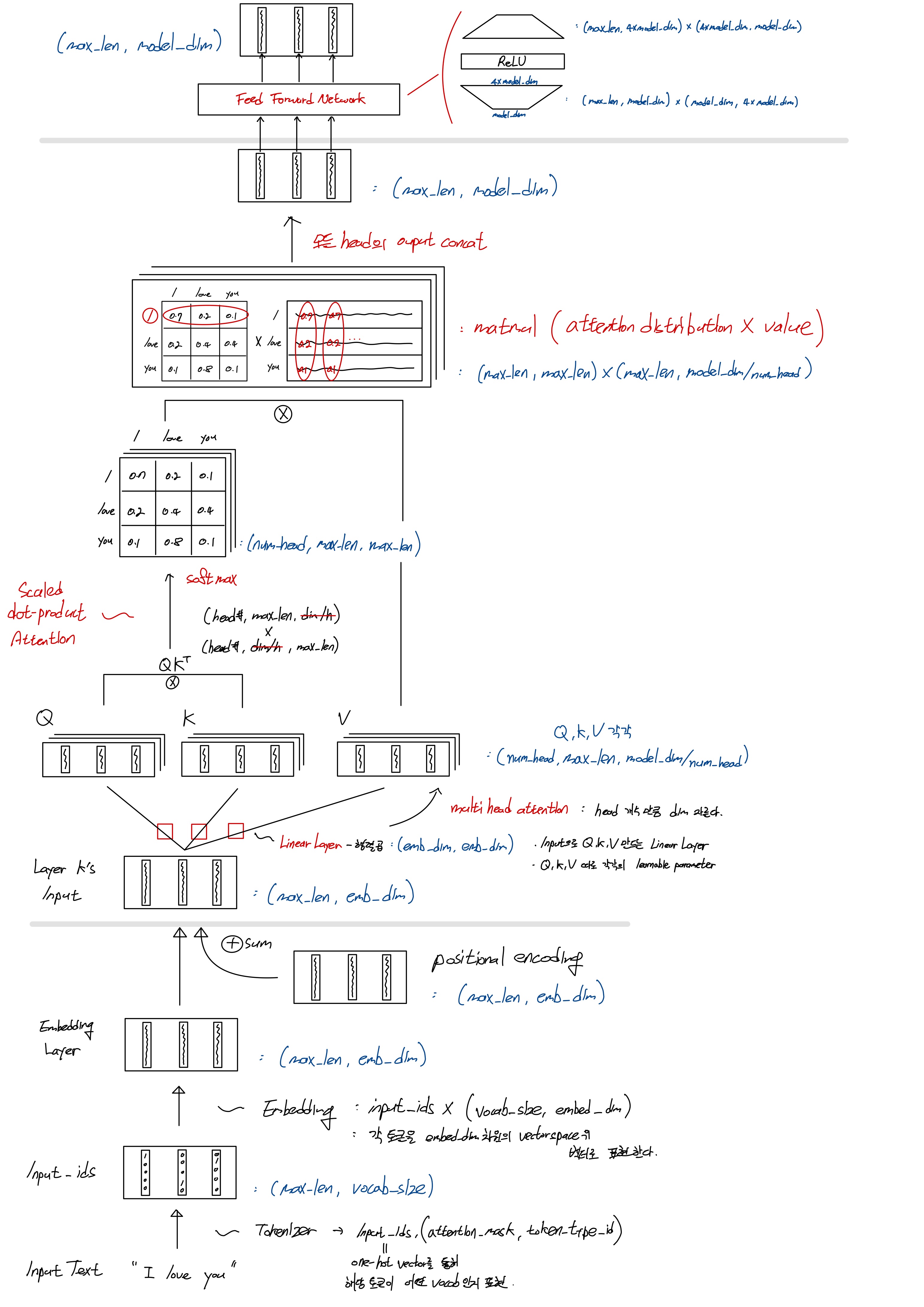
reference