[기초통계학]2. 확률

1. 표본공간과 사상

확률의 태동

• 계기: 우연한 사건이나 불확실한 현상에 대한 과학적 관심에서 비롯
• 발전: 어떤 사건의 가능성을 수리적으로 측정하는 노력
  - 16세기, 도박에서의 승률의 예상 그리고 배당금의 배분 문제를 풀기 위해 확률 개념이 만들어짐
  • 17세기, 페르마(Fermat)와 파스칼(Pascal)에 의해 초기의 확률 계산법이 제시
  • 18세기와 19세기 초반에 걸쳐 여러 학자들에 의해 중요한 개념과 원리가 개발되고, 20세기 초 공리적 정의가 만들어지면서 확률 이론의 기반이 자리잡게 됨

통계적 실험(statistical experiment)

데이터가 만들어지는 모든 활동을 다 아우르는 개념

• 예시: 동전을 던져 어느 면이 나오는지를 직접 확인, 성별이 남자인지 여자인지를 확인

확률실험

다음 세가지를 만족할 떄 확률실험 혹은 확률시행이라 함
1. (결과를 구하기 위한) 어떤 실험을 통해 나타나는 결과를 알지 못한다.
2. 결과는 알지 못하지만 결과로 나타날 수 있는 가능한 경우를 알고 있다.
3. 동일한 실험을 몇 번이고 반복할 수 있다.
예) 동전던지기
1. 동전을 던지기 전에 '앞면'이 나올지 '뒷면'이 나올지 알 수 없다.
2. 가능한 결과는 '앞면'과 '뒷면'중에 하나임을 알고 있다.
3. 동전을 던지는 실험은 몇 번이고 반복할 수 있다.

표본공간: S

확률실험(또는 관찰)을 실시하여 나타날 수 있는 모든 결과의 집합(S)

• 예시: 성별을 확인하는 실험에서의 표본공간: {남자, 여자}
  표본공간이 어떻게 정해지느냐에 따라 사건 크기의 비율이 달라지면서 확률도 달라지게 됨

원소(element)

• 표본공간을 구성하고 있는 요소
• 확률실험에서 나올 수 있는 각각의 결과

사상(event) - 사건

표본공간을 구성하고 있는 원소 중에서 관심의 대상이 되는 원소들의 집합 통계적 실험을 진행했을 떄 나오는 결과(outcome)
표본공간의 하나의 원소로 구성된 사건, 즉 부분집합(subset)
예시) 동전을 던지는 실험을 하였을 때 앞면이 나옴, 성별을 확인하는 실험을 하였을 때 남자라는 결과나 나옴
하나의 사건이 나타날 가능성을 수치로 나타낸 것이 확률(probability)

사상의 기본 연산

• 여사상 (complement): 사건A가 발생하지 않을 사건
  
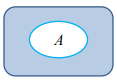
• 교사상 (intersection): 어떤 사건 발생이 사건 A와 사건 B에서 동시에 일어나는 사건
  
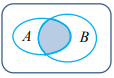
• 합사상 (union): 어떤 사건의 발생이 사건 A에서 일어나거나 혹은 사건 B에서 일어나는 사건
  
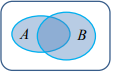
• 배반사건: 두 사건이 겹치는 부분이 없는 즉, 동시에 발생하지 않는 사건
• 독립사건: 두 사건이 서로의 발생에 영향을 끼치지 않는 사건

예) 주사위 두 개를 동시에 던지는 확률실험
A=눈금의 합이 짝수 B=눈금의 합이 8이상 C=눈금 차이가 1이하

# 표본공간 생성 (차례로 던지는 경우) => rolldie2(n) 함수
> S = rolldie2(2); nrow(S)
[1] 36

# 동시에 던지는 경우 => 순서 무시됨 => 표본공간 축소 => subset(n) 함수
> S2 = subset(S, X1 <= X2); nrow(S2)
[1] 21

# 표본공간 정렬 (X2, X2 순으로) => order() 함수
> S2 = S2[order(S2$X1,S2$X2),]

# subset() 함수를 사용하여 사상 정의
# 사상 A (합이 짝수) ⇒ (x %% y) 함수 ⇒ x를 y로 나눈 나머지
> A = subset(S2, ((X1+X2) %% 2)==0); element(A, 20)
(1,1) (1,3) (1,5) (2,2) (2,4) (2,6) (3,3) (3,5) (4,4) (4,6) (5,5) (6,6)

# 사상 B (합이 8 이상)
> B = subset(S2, (X1+X2) >=8); element(B)
(2,6) (3,5) (3,6) (4,4) (4,5) (4,6) (5,5) (5,6) (6,6)

# 사상 C (눈금 차이가 1 이하)
> C = subset(S2, abs(X1 - X2)<=1); element(C, 20)
(1,1) (1,2) (2,2) (2,3) (3,3) (3,4) (4,4) (4,5) (5,5) (5,6) (6,6)

# 교사상(intersection) ⇒ intersect2( ) 함수
> AB = intersect2(A, B); element(AB)
(2,6) (3,5) (4,4) (4,6) (5,5) (6,6)
> AC = intersect2(A, C); element(AC)
(1,1) (2,2) (3,3) (4,4) (5,5) (6,6)
> BC = intersect2(B, C); element(BC)
(4,4) (4,5) (5,5) (5,6) (6,6)
> ABC = intersect2(A, BC); element(ABC)
(4,4) (5,5) (6,6)

# 여사상(complement) ⇒ setdiff2( ) 함수 사용
> Bc = setdiff2(S2, B); element(Bc, 20)
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (2,2) (2,3) (2,4) (2,5) (3,3) (3,4)

# 교사상(intersection)
> ABc = intersect2(A, Bc); element(ABc)
(1,1) (1,3) (1,5) (2,2) (2,4) (3,3)

# 사상 A (눈금의 차가 3 이상)
> A = subset(S2, abs(X1-X2)>=3); Ae = element(A)
(1,4) (1,5) (1,6) (2,5) (2,6) (3,6)

# 사상 B (눈금의 곱이 20 이상)
> B = subset(S2, X1*X2 >= 20); Be = element(B)
(4,5) (4,6) (5,5) (5,6) (6,6)

# 상호배반인지 확인 ⇒ 교사상의 원소가 없으므로 상호배반임
> intersect2(Ae, Be)
character(0)

2. 확률의 정의

고전적 확률(classical probability) - 수학적 확률, 이론적 확률

동전을 던져 앞면이 나올 확률은 1/2라고 예상

• 기본 개념
  - 라플라스(Laplace) 시대에 나온 가장 오래된 확률의 정의
  • 두 가지 핵심 가정
    1. 하나의 표본공간은 유한 개의 사건들의 합집합으로 표현할 수 있다.
    2. 어떤 실험에서 각각의 사건이 일어날 가능성은 같다.
  • 확률의 정의: P(A) = n(A) / n(S) = n / N
    • 예) 주사위를 굴려 홀수가 나올 확률
      - 주사위의 각 눈이 나올 확률은 전체 6개의 눈으로 구성되어 있으며 각각이 나올 확률은 동일하다고 가정하면 확률은 1/6이다.
      - 홀수인 사건을 구성하는 근원사건의 수는 {1, 3, 5}으로 세 개가 있다.
      - 전체 눈의 개수는 6이고 이로부터 홀수 눈의 확률은 3/6 = 1/2이다.

상대도수(relative frequency) 확률- 통계적 확률, 경험적 확률

동전을 실제로 던져 보고 앞면이 나오는 횟수의 비율(상대도수)로 정하는 확률

• 기본 개념
  - n 번의 실험에서 특정 사건 A가 발생한 횟수 a를 무한대에 가깝게 반복했을 경우의 극한 값
  • 고전적 확률과 달리 확률을 미리 정의하지 않고 많은 실험의 경험을 바탕으로 사후적으로 계산
  • 확률의 정의

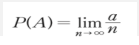
대수의 법칙(law of large numbers)

확률 실험(시행)을 무수히 반복 하면, 상대도수 확률이 고전적 확률과 점차 가까워짐

예) 공정한 동전을 각각 1회 ~ 500회씩 던져서 앞면이 나올 확률 추정

# 패키지 ‘animation' 설치 & # 설치가 끝난 후 패키지 ‘animation' 불러옴
> install.packages("animation")
> library(animation)

# 패키지 ‘animation' 옵션 설정 (최대 시행횟수, 시간간격) & # 창 크기 조정
> ani.options(nmax = 500, interval = 0.01); win.graph(7,4)

# 대수의 법칙 ⇒ lln.ani() 함수 실행 [그림 3-3]
> lln.ani(FUN = function(n, mu) rbinom(n, size=1, prob = mu), mu = 0.5, type="n", col.poly="blue")

# 제목, 격자 표시
> title(main="Law of Large Numbers (동전 던지기)"); grid()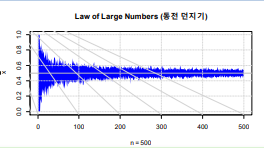

확률(probability)

어떤 사상이 발생할 수 있는 가능성을 수치로 나타낸 것
표본 공간의 모든 원소가 동일한 발생확률을 갖는다면, 사상 A의 확률은 전체 원소의 개수에 대한 사상 A에 속한 원소의 개수의 비율

확률의 특성

P(S) = 1, 0 <= P(A) <= 1, P(Ø) = 0

예) 공정한 동전을 네 번 던지는 실험에서, 앞면이 두 번 이상 나올 확률
S = {HHHH, HHHT, HHTH, ..., TTTH, TTTT} => |S| =2^4= 16
|A| = 4C4 + 4C3 + 4C2 = 1 + 4 + 6 = 11 => P(A) = 11/16 = 0.6875

# 표본공간 생성 및 정렬
> S = tosscoin2(4); S = S[order(S$X1, S$X2, S$X3, S$X4),]

# 표본공간 원소 출력 (한 줄에 8개 씩)
> element(S, 8)
(H,H,H,H) (H,H,H,T) (H,H,T,H) (H,H,T,T) (H,T,H,H) (H,T,H,T) (H,T,T,H) (H,T,T,T) 
(T,H,H,H) (T,H,H,T) (T,H,T,H) (T,H,T,T) (T,T,H,H) (T,T,H,T) (T,T,T,H) (T,T,T,T)

# 앞면의 개수를 세는 함수 정의
> counth = function(x) sum(x=="H")

# 앞면이 두 번 이상 나오는 사상 (한 줄에 6개 씩 출력)
> A = subset(S, apply(S, 1, counth)>=2); element(A, 6)
(H,H,H,H) (H,H,H,T) (H,H,T,H) (H,H,T,T) (H,T,H,H) (H,T,H,T) 
(H,T,T,H) (T,H,H,H) (T,H,H,T) (T,H,T,H) (T,T,H,H)

# 확률 계산 ⇒ pprt() 함수; nrow() 함수는 행의 개수(원소의 개수)를 구함
> pprt(A, nrow(S))
P(A) = 11 / 16 = 0.6875

예) 주사위 네 개를 동시에 던지는 실험
① A= 숫자의 합이 15 ② B= 한 개 이상의 6 ③ C= 한 개 이상의 1
④ P(A∩B), P(A∩C), P(B∩C), P(A∩B∩C)

# 표본공간 생성 (원소의 개수가 많아 나열하지 않음)
> S = rolldie2(4); (N= nrow(S)) [1] 1296

# (1) 숫자의 합이 15 이상인 사상의 확률 출력 ⇒ pprt() 함수
> A = subset(S, X1+X2+X3+X4 >=15); pprt(A, N) P(A) = 575 / 1296 = 0.4436728

# (2) 한 개 이상의 6이 나오는 사상 (행(원소) 별로 최댓값 적용)
> B = subset(S, apply(S, 1, max)==6); pprt(B, N) P(B) = 671 / 1296 = 0.5177469

# (3) 한 개 이상의 1이 나오는 사상 (행(원소) 별로 최솟값 적용)
> C = subset(S, apply(S, 1, min)==1); pprt(C, N) P(C) = 671 / 1296 = 0.5177469

# (4) 교사상(intersection) ⇒ intersect2() 함수
> AB=intersect2(A,B); AC=intersect2(A,C); BC=intersect2(B,C); ABC=intersect2(AB,C)
> pprt(AB, N); pprt(AC, N); pprt(BC, N); pprt(ABC, N)
P(AB) = 453 / 1296 = 0.349537
P(AC) = 140 / 1296 = 0.1080247
P(BC) = 302 / 1296 = 0.2330247
P(ABC) = 124 / 1296 = 0.09567901

예) 네 개의 주사위를 동시에 던지는 실험에서 네 개의 연속되는 숫자가 나올 확률

# sort()는 오름차순 정렬 함수, diff()는 원소 차이 계산 함수
# all()은 모든 원소가 참일 때 참(TRUE)이 되는 함수
# is.stra() 함수는 모든 원소가 연속되는 숫자인 경우에만 참(TRUE)이 됨
is.stra = function(x) all(diff(sort(x))==1)
stra = subset(S, apply(S, 1, is.stra)); nrow(stra)
[1] 72
# 연속숫자가 나올 확률 표시
pprt(stra, nrow(S))
P(stra) = 72 / 1296 = 0.05555556

역확률

정의

• 배경: 사건 A가 일어난 것을 전제로 한 사건 B의 조건부 확률 P(B|A)에 대해, 반대로 사건 B가 일어난 것을 전제로 한 사건 A의 조건부 확률 P(A|B)가 가능
• 역확률: 조건부 확률 P(A|B)가 조건부 확률 P(B|A)의 역확률(inverse probability)
  조건부 확률 P(A|B) <-> 역확률 P(B|A)

관계

• 조건부 확률과 역확률의 관계
  • P(B|A) = P(B∩A) / P(A), P(A|B) = P(A∩B) / P(B)
  • P(B|A) ⅹ P(A) = P(B∩A), P(A|B) ⅹ P(B) = P(A∩B)
  • P(A|B) ⅹ P(B) = P(B|A) ⅹ P(A)
  • 양쪽을 P(B)로 나누면 다음과 같은 관계가 성립
  

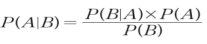
베이즈 정리

정의

• 좁은 의미: 사건 A, B에서 조건부 확률 P(B|A)와 그것의 역확률 P(A|B) 사이의 관계를 설명하는 정리
• 넓은 의미: 하나의 사건 B는 그대로 두고, 사건 A를 다시 여러 개의 작은 사건으로 나눈 후 사건 B와 사건 A1의 관계, 사건 B와 A2의 관계 등으로 펼치는 정리

과정

• 단계1: 분할(partition)
  - 전체의 표본공간 S는 두 개의 사건 A1과 A2로 이루어짐
  - A1과 A2는 서로 배타적인 관계
  - A1과 A2를 합치면 전체의 표본공간 S

  • 이 경우 A1과 A2가 S를 분할

• 단계2: 전확률 법칙(law of total probability)
  - P(B) = P(A1∩B) + P(A2∩B)
  - P(A1∩B) = P(B|A1)P(A1)
  - P(A2∩B) = P(B|A2)P(A2)

  • 따라서 P(B) = P(A1∩B) + P(A2∩B) = P(B|A1)P(A1) + P(B|A2)P(A2)

• 단계3: 베이즈 정리(Bayes' Theorem)
  - 위의 관계와 법칙을 바탕으로 다음과 같은 베이즈 정리 도출
  - 곱셈 법칙과 교환 법칙에 의해 P(A1∩B) = P(B∩A1) = P(B) ⅹ P(A1|B)
  - 전확률 법칙에 따라
  - P(B) = P(A1∩B) / P(B|A1)P(A1) + P(B|A2)P(A2)가 성립
  - P(A1∩B) = P(B|A1) P(A1)
  - 베이즈 정리 도출
  
  

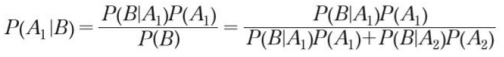
베이즈 정리의 확장

• 두개의 사건에서 A1, A2, A3, A4의 네개의 사건이 S를 분할하는 경우로 확장
• 사건 B가 일어난 후에 첫 번째 사건 A1이 일어나는 조건부 확률 P(A1|B)
  - P(A1|B) = P(A1∩B) / P(B) = P(A1)P(B|A1) / P(B)
• 분모의 P(B)는 다음과 같이 A1, A2, A3, A4와의 교집합의 합이 됨
• 따라서 베이즈 정리는 다음과 같이 확장됨
  • P(A1|B) = P(A1)P(B|A1) / P(B|A1)P(A1)+P(B|A2)P(A2)+P(B|A3)P(A3)+P(B|A4)P(A4)
  • P(A2|B) = P(A2)P(B|A2) / P(B|A1)P(A1)+P(B|A2)P(A2)+P(B|A3)P(A3)+P(B|A4)P(A4)
  • P(A3|B) = P(A3)P(B|A3) / P(B|A1)P(A1)+P(B|A2)P(A2)+P(B|A3)P(A3)+P(B|A4)P(A4)
  • P(A4|B) = P(A4)P(B|A4) / P(B|A1)P(A1)+P(B|A2)P(A2)+P(B|A3)P(A3)+P(B|A4)P(A4)