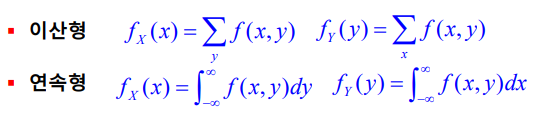확률변수와 확률분포의 개념
확률변수(random variable)
- 표본공간의 각 원소를 실수 값으로 바꾸는 함수
- 확률분포를 가짐
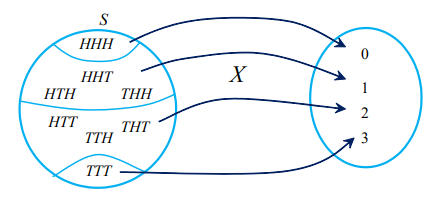
- 동전을 세 번 던지는 실험에서의 표본공간
-> S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT} - 동전의 뒷면이 나오는 횟수 -> 확률 변수
이산표본공간(discrete sample space)
유한개 또는 셀 수 있는 무한개의 원소로 구성된 표본공간
- 이산확률변수(discrete random variable)
- 동전의 앞면이 나올 때까지의 시행 횟수- 100개의 제품중 불량품의 수
연속표본공간(continuous sample space)
실직선 상의 임의의 구간으로 나타낼 수 있는 표본공간
- 연속확률변수(continuos random variable)
- 사람의 키와 몸무게- 제품의 수명
이산확률분포(discrete probability distribution)\
이산표본공간의 확률변수로부터 생성된 확률분포
-
확률질량함수(probability mass function)
P(X=x) = f(x)
Σf(x) = 1, 0<=f(x)<=1 -
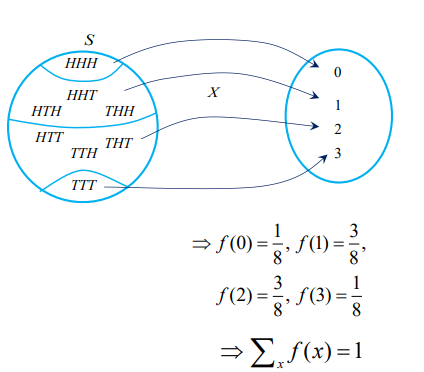
예) 동전을 세 번 던지는 시행에서의 뒷면의 개수 X의 확률 분포
# 표본공간 생성
> S = tosscoin2(3)
# 뒷면의 개수를 세는 함수 정의
> countT = function(x) sum(x=="T")
# 확률변수 정의 => apply() 함수를 행별로 적용
> X = apply(S, 1, countT)
# 원소의 개수 집계 및 확률분포 생성
> table(X)/nrow(S)
X
0 1 2 3
0.125 0.375 0.375 0.125- 예) 주사위를 네 번 던지는 실험에서 나오는 숫자 합 X의 확률분포
# 주사위 4개의 눈의 합 확률분포
rolldie.sum(4)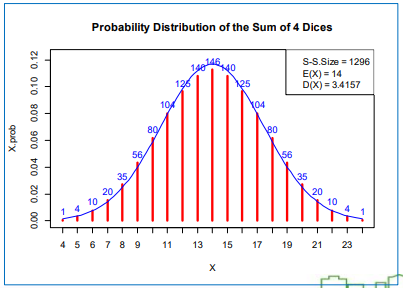
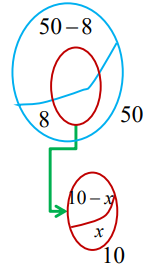
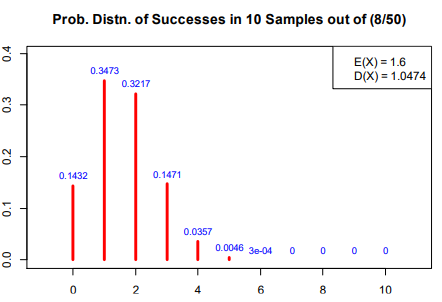
- 예) 50개의 제품 중 8개의 불량품이 있는 상자로부터 10개의 제품을 랜덤 샘플링했을 때, 발견되는 불량품 개수 X에 대한 확률분포
hyp.sample(50, 8, 10)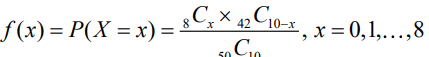
연속확률분포(continuous probability distribution)
- 연속적인(셀 수 없는) 값을 갖는 확률변수의 확률분포
- 확률분포함수 f(x)는 확률 P(a<X<b)를 구하기 위한 확률밀도 함수
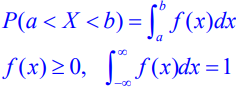
# 확률밀도함수 f(x) 정의
> pdf = function(x) 2*exp(-2*x)*(x>0)
# 적분함수 integrate() 사용하여 확률 계산
> integrate(pdf, 0, 1)[[1]]
[1] 0.8646647누적분포함수(cumulative distribution function)
확률변수 X가 특정한 값 x 이하일 확률
F(x) = P(X<=x)
- 확률분포의 누적분포함수(cumulative distribution function)는 이산형과 연속형의 구분 없이 다음과 같이 정의된다.
-> 누적분포함수 F(x)는 확률변수의 값이 x이하일 확률임 단, 이산확률 분포에서는 누적확률분포의 등호에 주의하여 확률을 계산할 필요가 있음 - 예) 동전을 세 번 던지는 확률실험에서 뒷면의 개수 X에 대한 누적분포함수
# 동전 3개 중 뒷면의 개수
> (freq = choose(3, 0:3))
[1] 1 3 3 1
disc.cdf(0:3, freq, mt = "동전 3개 중 뒷면의 개수 CDF")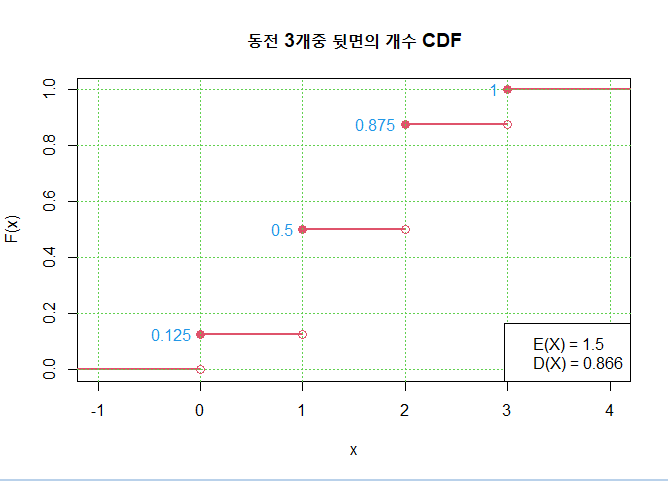
- 예) 연속확률 분포의 CDF f(x)= 2e^-2, 0<x<∞인 경우 누적 분포함수 F(x)를 구하시오
# 확률밀도함수 f(x) 정의 및 누적분포함수 그래프 작성
> pdf = function(x) 2*exp(-2*x)*(x>0)
# 누적 확률 표시 (F(0.2), F(0.4), F(0.6), F(0.8), F(1), F(2))
cont.cdf(pdf, low=-1, up=3, xs=c((1:5)*0.2, 2))결합확률분포 (joint prob, dist. function)
두 개 이상의 확률변수를 다루어야 할 때는 확률변수 간에 서로 영향을 주고받을 수 있으므로 동시에 고려할 필요가 있음
- 2개 이상의 확률변수에 대한 확률분포
- 이산형 결합확률분포
두 확률변수 X와 Y가 동시에 각각 x와 y의 값을 가질 확률
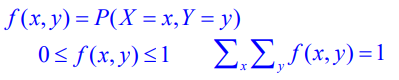
- 연속형 결합확률분포
두 확률변수 X와 Y의 확률을 계산하기 위한 밀도함수
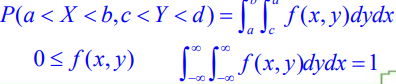
주변확률분포(marginal probability distribution)
확률변수 x와 y의 결합확률분포 f(x,y)로부터 각각의 주변확률분포(marginal probability distribution)는