[머신러닝] Markov Chain

Markov Chain

마코프 체인(Markov)은 마코프 성질(Markov Property)을 지닌 이산 확률 과정(Stochastic Process)을 의미합니다.

Markov Property

마코프 성질 : n+1회의 상태(state)는 오직 n회에서의 상태 혹은, 그 이전 일정 기간의 상태에만 영향을 받는 것을 의미합니다. 예를 들면 동전 던지기는 독립 시행이기 때문에 n번째의 상태가 앞이던지 뒤이던지 간에 n+1번째 상태에 영향을 주지 않습니다. 하지만 1차 마르코프 체인은 n번째 상태가 n+1번째 상태를 결정하는데 영향을 미칩니다.

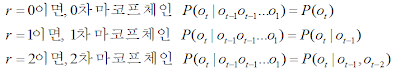
Markov Model

마코프 모델은 위의 가정하에 확률적 모델을 만든 것으로, 각 상태를 먼저 정의하게 됩니다. 상태 (state) 는 V={v1, ...vm)으로 정의하고, m개의 상태가 존재합니다. 그 다음은 상태 전이 확률(State transition Probability) 을 정의할 수 있습니다. 상태 전이 확률이란 각 상태에서 각 상태로 이동할 확률을 말합니다. 상태 전이 확률 aij는 vi에서 상태 vj로 이동할 확률을 말합니다. 아래의 식은 상태 전이 확률을 식으로 나타낸 것과 그 아래는 확률의 기본 정의에 의한 상태 전이 확률의 조건입니다.

Example

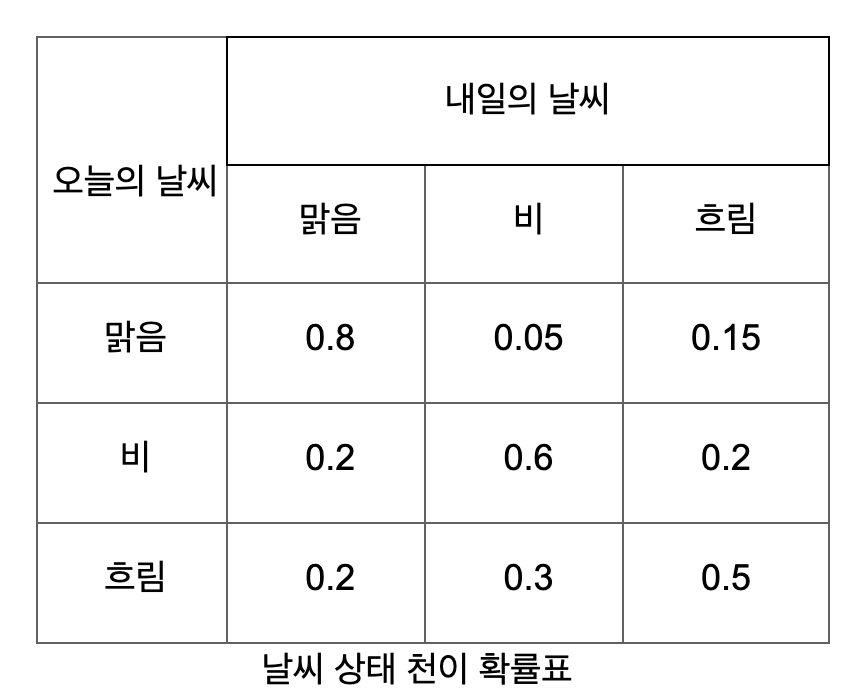
1차 마코프 가정을 이용하여 확률을 계산해봅시다.

날씨 영역은 세 가지 상태 (S={맑음, 비, 흐림})을 나타냅니다.
그리고 날씨는 전이 확률표와 같이 확률값 P(qn | qn-1)에 따라 다른 상태로의 전이가 이루어집니다.

오늘 날씨(q1)가 '맑음'일 경우에 내일 날씨(q2)가 '맑음'이 되고 모레 날씨(q3)가 '비'가 될 확률은 얼마일까요?

    P(q2=맑음, q3=비 | q1=맑음)
      = P(q3=비 | q2=맑음, q1=맑음) ·P(q2=맑음|q1=맑음)
      = P(q3=비 | q2=맑음)·P(q2=맑음|q1=맑음)    <- 마코프 가정
      = 0.05 x 0.8
      = 0.04

위 계산 과정에서 1차 마코프 가정에 의해

    P(q3=비 | q2=맑음, q1=맑음) = P(q3=비 | q2=맑음)

가 됩니다.

그렇다면 어제, 오늘의 날씨가 각각 q1=비, q2=흐림 일 때, 내일 날씨가 q3= 맑음 이 될 확률은 얼마일까요?

    P(q3=맑음  | q2=흐림, q1=비)
      = P(q3=맑음 | q2=흐림)    <- 마코프 가정
      = 0.2