
Intro
JS는 객체지향과 더불어 함수형 프로그래밍도 가능한 언어다.
함수형 프로그래밍을 이해하기 위해 함수부터 필요한 개념들을 다시 정리하고 객체지향 예제 코드를 함수형으로 개선하면서 함수형 프로그래밍에 대해 이해해보자.
🌱 학습 키워드
함수란?
input을 받아 output을 내보내는 수학의 함수와 같은 개념이다.

함수 내부로 입력을 전달받는 변수를 매개변수(파라미터), 입력을 인수, 출력을 반환값이라 한다.
const result = add(2,5)와 같이 함수 호출로 인수(2,5)를 전달하면 반환값(7)을 반환한다.
- 함수는 호출을 통해 언제든 재사용이 가능하다.
- 수정과 유지보수의 편의성을 위해 중복되는 코드를 최대한 함수로 표현하는 것은 필수적이다.
- 매개변수의 개수나 순서가 변경되면 함수 호출 방법이 바뀌기에 유지보수성이 나빠진다.
- 또 코드의 가독성에 방해되기에 이상적인 매개변수 개수는 0개이며 적을수록 좋다.
- 매개변수가 많다는 것은 함수가 여러가지 일을 한다는 증거가 된다.
- 이상적인 함수는 한 가지 일만 해야 하며 가급적 작게 만들어야 한다.
일급객체(일급함수)
값처럼 변수에 할당 할 수도 있고 프로퍼티 값이 될 수도 있으며 배열의 요소도 될수 있는 객체.
JS에서의 함수도 일급객체해 해당한다. 즉, 함수를 값처럼 자유롭게 사용할 수 있다.
함수 선언문 vs 함수 표현식
//함수 선언문
function add(x, y) {
return x + y;
}
// 함수 표현식
const add = function (x, y) {
return x + y;
};함수 선언문은 함수 호이스팅으로 선언문 이전에 함수를 호출할 수 있다.
이는 런타임 이전에 함수 객체가 생성되고 객체를 할당했다는 것으로,
변수 호이스팅과는 다르게 undefined로의 초기화가 아닌 함수 객체로의 초기화를 뜻한다.
-> 즉 함수가 호출 되지 않았는데도 선언되어 잘 실행된다는 것이다. (호출 전에 선언이라는 규칙을 무시한다.)
반면에 함수 표현식은 변수 호이스팅과 같이 undefined를 초기화 한다.
즉 호출 전에 반드시 선언이 되어야 한다는 것이다.
에러는 개발자에게 좋은 지침이다. 함수 선언문이 아닌 표현식을 사용하도록 하자.
함수형 프로그래밍이란?
- 순수 함수를 통해 부수효과를 최대한 억제하여 오류를 피하고 프로그램의 안정성을 높이려는 프로그래밍 패러다임.
- 순수 함수와 보조 함수의 조합을 통해 외부 상태를 변경하는 부수효과를 최소화해서 불변성을 지향하는 프로그래밍.
- 로직 내에 존재하는 조건문과 반복문을 제거해서 복잡성을 해결하며,
- 변수 사용을 억제하거나 생명주기를 최소화해서 상태 변경을 피해 오류를 최소화하는 것을 목표로 한다.
- "함수형 프로그래밍은 애플리케이션, 함수의 구성요소, 더 나아가서 언어 자체를 함수처럼 여기도록 만들고, 이러한 함수 개념을 가장 우선순위에 놓는다."
"함수형 사고방식은 문제의 해결 방법을 동사(함수)들로 구성(조합)하는 것"
객체지향 vs 함수형
객체지향 : 데이터를 디자인하고 데이터에 맞는 메서드를 정의
함수형 : 함수를 만들고 그 함수에 맞게 데이터 셋을 구성
순수함수
- 외부 상태를 변경하지 않고 외부 상태에 의존하지도 않는 함수를 순수 함수라 한다.
- 순수 함수는 동일한 인수가 전달되면 언제나 동일한 값을 반환하는 함수다.
- 순수 함수는 일반적으로 최소 하나 이상의 인수를 전달 받는다. (인수가 없다면 상수가 된다.)
- 순수 함수는 인수를 변경하지 않는다. (인수의 불변성을 유지한다.)
- 순수 함수는 함수의 외부 상태를 변경하지 않는다.


콜백함수
함수의 매개변수를 통해 다른 함수의 내부로 전달되는 함수를 콜백 함수라고 한다.
function repeat(n ,f) {
for (var i = 0; i < n; i++>) {
f(i);
}
var logAll = function(i) {
console.log(i)
}
}
repeat (5, logAll); // 0 1 2 3 4고차함수
매개변수를 통해 함수의 외부에서 콜백 함수를 전달 받은 함수를 고차함수라고 한다.
매개변수를 통해 함수를 전달 받거나 반환값으로 함수를 반환하는 함수를 고차 함수라 한다.
function repeat(n ,f) {
for (var i = 0; i < n; i++>) {
f(i);
}
}
const logOdds = function (i) {
if (i % 2) console.log(i);
};
repeat(5, logOdds); // 1 3화살표 함수
화살표 함수는 함수 선언문으로 정의할 수 없고 함수 표현식으로 정의해야 한다.
호출 방식으 아래와 같다.
const add = (x, y) => x + y;
add(1,2) // 3화살표 함수는 항상 익명 함수로 정의한다.
불변성 (Immutable)
람다 계산법의 근간이 되는 개념은 심볼의 값이 변경되지 않는다는 것이다.
가변 변수를 사용하는 대신에 심볼에 값을 할당하면 그 값은 변경되지 않는다.
참조투명성과 부작용
순수 함수로 만들면 함수 외부에 값이나 객체를 참조하거나 의존적으로 동작하지 않기 때문에 참조투명성을 가지고, 부작용이 없다.
반대로 말하면 부작용이 있는 함수는 입력 값이 동일해도 함수 외부에 값에 따라서 다른 값이 리턴한다.
부수효과가 있는 함수는 순수함수가 아니다.
클로져
클로저는 독립적인 (자유) 변수 (지역적으로 사용되지만, 둘러싼 범위 안에서 정의된 변수)를 참조하는 함수들이다. 다른 말로 하면, 이 함수들은 그들이 생성된 환경을 ‘기억’한다.
여기서의 핵심은 환경이다.
자바스크립트 엔진은 함수를 어디서 호출했는지가 아니라 함수를 어디에 정의했는지에 따라 상위 스코프를 결정한다. 이를 렉시컬 스코프(정적 스코프)라 한다.
즉, 클로져는 함수가 생성(정의)된 환경(렉시컬스코프)을 기억한다.
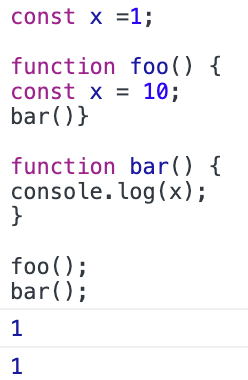
위 예제의 경우 두 함수 foo(), bar()가 생성(정의)된 스코프(환경)을 주목해야한다. 두 함수 모두 전역에서 정의되었기에 상위 스코프 또한 전역이 된다. 그래서 반환값은 전역의 x=1 값을 반환하고 있다.
말이 너무 어렵다. 간단하게 정리하자.
클로져(함수)는 자신이 정의된 환경을 기억하고 그 환경의 내부 슬롯이라는 공간에 자신을 저장한다.
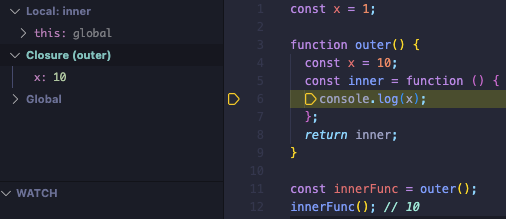
여기서 클로저는 inner = function() {console.log(x)}가 된다. 디버깅에서 보듯이 클로져는 outer() 스코프 안에서 정의되었고, 스코프 안에서 반환된 x = 10 값을 클로져 자신의 내부슬롯에 저장하고 있다.
그렇다고 모든 함수가 클로져가 될수는 없다.
클로져라는 개념이 생긴 이유는 외부함수(outer) 내에서 상위 스코프의 식별자를 참조하는 중첩함수(inner)가 외부함수(outer)가 종료된 후에도 저장하고 있던 값을 기억하기위해 만들어졌다.
클로져는 함수(외부함수)의 내부에서 또 다른 함수(중첩함수)가 정의되고 그 중첩함수로 만들어진 반환값을 외부함수가 종료된 후에도 사용하기 위해 만들어 졌다.
📝 함수형 프로그래밍 실습
아래 객체지향 ClassifierAlpha, PrimeAlpha 클래스 코드를 함수형 프로그래밍으로 개선해보고 2-100 까지의 숫자를 판별해보자.
class ClassifierAlpha {
number = 0;
constructor(number) {
this.number = number;
}
isFactor(potentialFactor) {
return this.number % potentialFactor == 0;
}
factors() {
var factorSet = new Set();
for (var pod = 1; pod <= Math.sqrt(this.number); pod++) {
if (this.isFactor(pod)) {
factorSet.add(pod);
factorSet.add(this.number / pod);
}
}
return factorSet;
}
isPerfect() {
return ClassifierAlpha.sum(this.factors()) - this.number == this.number;
}
isAbundant() {
return ClassifierAlpha.sum(this.factors()) - this.number > this.number;
}
isDeficient() {
return ClassifierAlpha.sum(this.factors()) - this.number < this.number;
}
static sum(factors) {
var total = 0;
factors.forEach((factor) => {
total += factor;
});
return total;
}
}
class PrimeAlpha {
number = 0;
constructor(number) {
this.number = number;
}
equalSet(aset, bset) {
if (aset.size !== bset.size) return false;
for (var a of aset) if (!bset.has(a)) return false;
return true;
}
isPrime() {
var primeSet = new Set([1, this.number]);
return this.number > 1 && this.equalSet(this.factors(), primeSet);
}
isFactor(potentialFactor) {
return this.number % potentialFactor == 0;
}
factors() {
var factorSet = new Set();
for (var pod = 1; pod <= Math.sqrt(this.number); pod++) {
if (this.isFactor(pod)) {
factorSet.add(pod);
factorSet.add(this.number / pod);
}
}
return factorSet;
}
}1차 시도
- 중복코드를 최대한 함수로 축소한다.
- 매개변수는 어떤 함수에서도 변경되지 않도록 한다.
- 새로운 변수를 최대한 배재하고 필요하더라고 let은 피한다.
- 조건문, 반복문을 피한다. (순수함수)
const getFactors = function (n) {
const factorSet = new Set();
const arr = Array.from({ length: Math.sqrt(n) }, (v, i) => i + 1);
arr.forEach((v) => {
if (isFactor(n, v)) {
factorSet.add(v);
factorSet.add(n / v);
}
});
return factorSet;
};
const isFactor = (n, v) => n % v === 0;
const sumFactors = (factorSet) => {
return (sum = [...factorSet].reduce((pre, cur) => pre + cur));
};
const checkKindNumber = function (n) {
const checkNumber = sumFactors(getFactors(n)) - n;
const perfect = checkNumber === n;
const abundant = checkNumber > n;
const deficient = checkNumber < n;
switch (true) {
case perfect:
return `Perfect`;
case abundant:
return `Abundant`;
case deficient:
return `Deficient`;
}
};
const setToArray = (set) => Array.from([...set]);
const equalSet = function (factorSet, primeSet) {
const factorArray = setToArray(factorSet).sort((a, b) => a - b);
const primeArray = setToArray(primeSet);
return factorArray.every((v, i) => v === primeArray[i]);
};
const isPrime = function (n) {
const primeSet = new Set([1, n]);
const prime = n > 1 && equalSet(getFactors(n), primeSet);
return prime ? `Prime` : "";
};
const print = function (n) {
const numberArray = Array.from({ length: n }, (v, i) => i + 2);
return numberArray.forEach((v) =>
console.log(`${v} : ${checkKindNumber(v)}, ${isPrime(v)}`)
);
};
console.log(print(99));2차 시도
- 1차 시도에서 제거못한 조건문을 제거
- forEach() 함수 제거
- 화살표 함수 적극 사용
- set을 array로 바꿔서 필요없는 코드 삭제
const getFactors = (n) => {
const numberSqrtArray = Array.from({ length: Math.sqrt(n) }, (_, i) => i + 1);
return (factorArray = numberSqrtArray
.filter((v) => isFactor(n, v))
.flatMap((v) => [v, n / v]));
};
const isFactor = (n, v) => n % v === 0;
const sumFactors = (factorArray) =>
(sum = factorArray.reduce((pre, cur) => pre + cur));
const equalSet = (factorArray, primeArray) => {
return factorArray.every((v, i) => v === primeArray[i]);
};
const isPerfect = (n) => sumFactors(getFactors(n)) - n === n;
const isAbundant = (n) => sumFactors(getFactors(n)) - n > n;
const isDeficient = (n) => sumFactors(getFactors(n)) - n < n;
const isPrime = (n) => (n > 1 ? equalSet(getFactors(n), [1, n]) : false);
const checkKindNumber = (v) => {
const perfect = isPerfect(v);
const abundant = isAbundant(v);
const deficient = isDeficient(v);
switch (true) {
case perfect:
return "Perfect";
case abundant:
return "Abundant";
case deficient:
return "Deficien";
}
};
const print = function (n) {
const result = Array.from({ length: n }, (_, i) => i + 2);
return result.reduce(
(_, pre) =>
console.log(
`${pre} : ${checkKindNumber(pre)}, ${isPrime(pre) ? "Prime" : ""}`
),
2
);
};
console.log(print(99));Outro
이번 함수형 프로그래밍을 공부하면서 내가 생각하던 함수형 프로그래밍은 완전히 잘못 되었구나를 크게 깨달았다. 함수의 개념부터 다시 정리하며 순수함수가 무엇인지 왜 순수함수를 추구하는지를 알게 되어 앞으로의 코딩에도 적극 적용하도록 해봐야겠다. 그리고 배열의 메서드로만 생각했던 map(), reduece(), filter() 등의 고차함수가 어떤 원리로 작동되는지도 알게되어 많은 연습이 되었다.
🛠️ 보완점
- 클로저 적극 활용해보기
- 카링에 대해 공부하기
- 파이프함수에 대해 공부하기
