참고자료
https://www.youtube.com/watch?v=X8SBsVqmVdY
https://greatjoy.tistory.com/51
https://www.simplilearn.com/tutorials/deep-learning-tutorial/what-are-autoencoders-in-deep-learning#what_are_autoencoders
https://gaussian37.github.io/dl-concept-autoencoder2/
https://needjarvis.tistory.com/454
https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote12.html
https://89douner.tistory.com/339(representation learning)
이번 포스팅을 이해하기 위해서 필요한 개념을 잘 담은 사진을 가져왔다
출처 : https://www.mobiinside.co.kr/2020/03/12/ai-perceptron/
Autoencoder란?
Autoencoder는 unlabeled data의 효과적인 코딩을 배우는데 사용되는 인공신경망의 한 형태이다. 구조는 Encoder와 Decoder가 bottleneck 구조를 이룬다. Encoder는 입력데이터를 의미있고(meaningful) 압축된 표현(representation)으로 인코딩한다. Decoder는 인코딩 된 representation을 다시 입력데이터로 복원시키는 일을 한다. 학습을 할 때는 입력 데이터만을 활용하는 Unsupervised learning으로 입력데이터와 복원된 데이터의 차이를 최소화 하는 방향으로 한다.
출처 : https://d1m75rqqgidzqn.cloudfront.net/wp-data/2020/04/29201743
무슨 목적으로 사용될까?
Manifold learning : 입력 데이터를 의미있고 압축된 representation으로 매핑해서 encoder 학습이 목적
Generative Model : 어떤 latent variable을 실제 data distribution으로 매핑해서 decoder 학습이 목적
Manifold
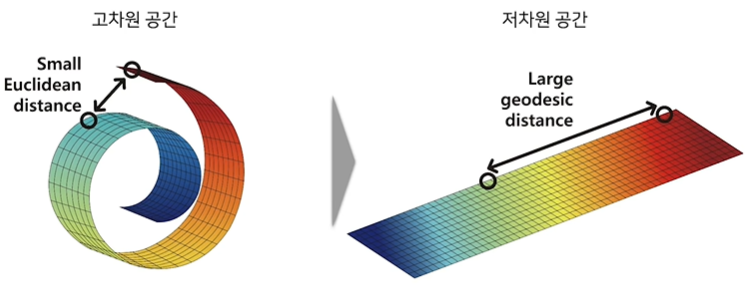
공간상에 데이터를 표현하면 각 데이터들은 점의 형태로 찍힐 것이다. Manifold는 이런 점들을 최대한 에러 없이 아우를 수 있는 서브 스페이스라고 정의한다. 데이터들은 각각 유클리디안 거리를 따르지만, 저차원으로 갔을때는 그것을 따르지 못할 경우도 있다. 즉, Manifold는 고차원 공간에 내재한 저차원 공간이라고 생각하면 된다.
출처 : https://velog.io/@sheoyonj/NN-Network-3
Manifold learning
Manifold learning은 고차원 공간의 데이터를 저차원 manifold 공간으로 mapping시키는 함수를 찾는 과정이다.
학습이 끝난 Autoencoder의 Encoder를 매핑 함수로 사용한다. 데이터들을 Manifold공간으로 매핑함으로써 dimensionality reduction, feature extraction, representation learning등의 역할을 수행한다.
Generative model
실제 데이터의 분포를 학습하여 데이터를 생성하는 생성모델로 대표적으로는 Generative Adversarial Networks(GAN)와 Variational Autoencoder(VAE)가 있음. Latent variable을 실제 데이터 분포로 mapping시키는 함수를 찾는 것이 목적이다.학습이 끝난 AutoEncoder의 decoder를 매핑 함수로 사용한다.
다양한 Autoencoder
Manifold learning에서 Autoencoder의 과적합 문제를 해결하기 위해 다양한 규제 기법을 적용하는 과정에서 여러 변형이 발생하였다.
- Sparse Autoencoder : AE + Sparsity regularization
- Denoising Autoencoder : AE + Random noise
- Contractive Autoencoder : AE + Jacobian Matrix
Bias-variance tradeoff in autoencoder
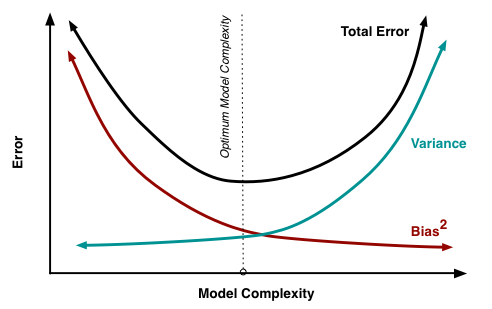
- Bias : 실제 데이터를 표현하는 모델과 가정한 모델의 차이에서 발생하는 오류, 실제값과 평균 예측값의 차이
- Variance : 모델링에 사용되는 여러 표본 데이터 집합에 대한 추정을 할 때 발생하는 오류, 예측값에 대한 분산
- Irreducible Error : 줄일 수 없는 자연적인 오류
출처 : cornell computer science
훈련집합과 검증집합 관점에서 훈련집합에 대한 오류율이 너무 작아지면 검증집합에 대한 variance가 커져 다른 표본집합에 대한 일반화 성능이 떨어지는 overfitting이 발생한다. 데이터에 알맞은 모델의 복잡도를 찾는 것은 매우 어렵다. 딥러닝은 모델의 복잡도를 높인 뒤, 다양한 규제 기법을 통해서 bias를 높이고 variance를 낮추는 방향으로 발전해왔다.
Sparse Autoencoder
Hidden layer의 노드 수가 input layer의 node 수보다 많은 overcomplete autoencoder 구조이다. Sparsity parameter를 제어하여 은닉층의 활성화에 규제를 가하는 방법을 사용한다.
출처 : https://data-newbie.tistory.com/180
Denoising Autoencoder
입력 데이터에 random noise나 dropout을 추가하는 규제기법을 적용한다. 입력 데이터에 어떠한 노이즈를 주어도 manifold 상에서 같은 곳에 위치해야 한다는 가정이다. 입력 데이터에 작은 변화를 주어 손상된 데이터를 만들고 모델을 통해 손상되지 않은 데이터를 출력하는 방법으로 이를 통해 작은 변화에 대해 덜 민감하고 강건한 모델을 만들 수가 있다.
Contractive Autoencoder
Denoising Autoencoder와 같이 작은 변화에 강건한 모델을 학습하는 것이 목적이다. Denoising Autoencoder에서는 입력 데이터의 작은 변화에 저항하도록 하는 데 중점을 두었다면 여기서는 중요하지 않은 입력의 변화를 무시하도록 하여 특징을 추출할 때 작은 변화에 덜 민감하도록 하는 것에 중점을 두었다.
Autoencoder의 활용(Manifold learning)
Classfication
AutoEncoder를 통해 학습시킨 인코더를 Feature extractor로 사용하여 self-supervised learning 혹은 semi-supervised learning에 활용하였다. 같은 Class를 가지는 관측치들은 드러나지 않았지만 autoencoder를 통해 이를 근사할 수 있는 latent structure가 있을 것(의미있는 represenation)이라 가정한다.
Clustering
비슷한 Unlabeled data간에는 숨겨진 row-dimensional latent representation(manifold)가 존재할 것이라는 가정으로 학습시킨 인코더를 통해 Unlabeld data를 임베딩한다. 임베딩된 관측치를 이용해 기존의 군집화 알고리즘을 통해 군집화를 할 수 있다.
Anomaly detection
정상 관측치와 이상 관측치 간에 latent structure가 다를 것이라 가정하고, 정상 관측치만을 학습데이터로 사용하고 Autoencoder가 이상 관측치는 잘 복원하지 못할 것이라는 기대를 갖는다. 비정상 관측치가 입력된다면 reconstruction loss가 클 것이라고 예상한다.
dimensionality reduction
실제 데이터(이미지, 텍스트)들은 매우 높은 차원의 sparse한 벡터로 표현되는 경우가 많다. 이런 고차원 벡터들을 통해 학습을 하게 되면 curse of dimensionality에 빠질 수 있다. 이를 해결하기 위해 데이터들을 훨씬 낮은 차원의 intrinsic dimensionality(본질적 차원)으로 매핑시키는 것이 목적이다.
