SVM(Support Vector Machine)

Hun·2023년 8월 22일
머신러닝
0

머신러닝

목록 보기
2/2

참고자료

https://www.youtube.com/watch?v=_PwhiWxHK8o
https://sanghyu.tistory.com/7
https://en.wikipedia.org/wiki/Support_vector_machine
https://jaejunyoo.blogspot.com/2018/01/support-vector-machine-1.html#mjx-eqn-eqdr
https://decisionboundary.tistory.com/2

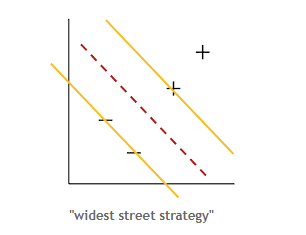출처 : https://jaejunyoo.blogspot.com/2018/01/support-vector-machine-1.html#mjx-eqn-eqdr

SVM이란?

SVM은 두 개의 집단을 분류를 선형적으로 분류를 한다. 다른 분류 기법과는 다르게 위의 사진과 같이 두 집단 사이의 여백(margin)이 가장 넓어지도록 분류한다.그럼 어떻게 하면 가장 잘 분류할 수 있는 기준을 알 수 있을까? 먼저 SVM의 decision rule을 알아보기전에 간단한 용어 정리부터 해보자.

support vector : '+' sample과 '-' sample 들이 모인곳에서 최외각에 있는 sample을 support vector라고 한다. 이 벡터들을 기준으로 margin을 구한다.
hyper plane : 어떤 N차원 공간에서 한 차원 낮은 N-1차원의 subspace를 뜻함

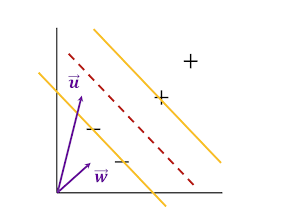출처: https://jaejunyoo.blogspot.com/2018/01/support-vector-machine-1.html#mjx-eqn-eqdr

SVM decision Rule

위의 그림에서 ww는 support vector 사이의 여백을 가장 크게하는 방향을 뜻한다. 크기는 우선 상관하지 않는다. uu는 임의의 vector를 뜻한다. 두 벡터를 내적시킨다면

w‾⋅u‾+b≥0then′+′\overline{w} \cdot \overline{u} +b \geq 0 \qquad then \quad'+'

이 식을 구할 수 있다. 이것을 통해 알 수 잇는 것은 위 식이 0보다 같거나 크면 u가 '+' 영역에 있고 0보다 같거나 작으면 -샘플 쪽에 있다는 것을 알 수 있다. 하지만,여기서 어떤 기준으로 ww와 bb를 잡아야 하는지 모른다. 이를 위해 몇가지 조건을 더 건다.

w‾⋅x++b≥1w‾⋅x−+b≤−1\overline {w} \cdot {x_+} + b \geq 1 \\ \overline {w} \cdot {x_-} + b \leq -1

여기서 복잡한 식을 줄이기 위해 새로운 변수를 추가해 다시 정의한다.

yi={1for ′+′−1for ′−′y_i = \begin{cases} 1 \quad &\text{for }\quad '+' \\ {-1} \quad&\text{for } \quad'-' \end{cases}

양변에 yiy_i를 곱해주면

yi(w‾⋅xi‾+b)≥1yi(w‾⋅xi‾+b)−1≥0y_i(\overline {w} \cdot \overline{x_i} + b ) \geq 1\\ y_i(\overline {w} \cdot \overline{x_i} + b ) -1 \geq 0

으로 정리할 수 있다. 상황에 따라 복잡했던 식을 하나의 간단한 식으로 만들었다. 이 때, xx를 노란선 위에 있다고 가정을 하면,

yi(w‾⋅xi‾+b)−1=0y_i(\overline {w} \cdot \overline{x_i} + b ) -1 = 0

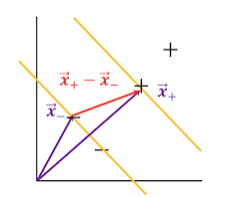출처: https://jaejunyoo.blogspot.com/2018/01/support-vector-machine-1.html#mjx-eqn-eqdr

이된다. 우리는 가장 최대의 margin을 구하는것이 목표이다. 폭을 구하려면 각 영역에 있는 support vector의 차를 ww의 단위벡터와 내적을 시키면 알 수 있다.

Width=(x+−x−)⋅w‾∥w∥Width = (x_+ - x_-) \cdot {{\overline {w}} \above{1pt}\lVert {w} \rVert}

그리고 위에서 간단하게 정리한 식을 대입하면

Width=2∥w∥Width = { {2} \above{1pt}\lVert {w} \rVert}

폭을 알았으니 이 값이 최대값이 이루어지면 된다.

max1w‾→min∥w‾∥→min12∥w‾∥2max {1\above{1pt}{\overline w}} \rightarrow min\lVert {\overline w} \rVert \rightarrow min {1\above{1pt}2}\lVert {\overline w} \rVert^2

이 과정은 모두 수학적 편의를 위해서이다. 위의 정의한 조건들을 라그랑주 승수법을 활용해 신경쓰지 않고 풀 수 있다. 라그랑주 승수법은 간단히 말하자면 모든 제약식에 라그랑주 승수(Lagrange Multiplier) λ를 곱하고 등식 제약이 있는 문제를 제약이 없는 문제로 바꾸어 문제를 해결하는 방법이다. 아래 식에서는 α\alpha를 뜻한다.

L=12∥w‾∥2−∑αi[yi(w‾⋅xi‾+b)−1]L = {1\above{1pt}2}\lVert {\overline w} \rVert^2 - \sum\alpha_i[y_i(\overline {w} \cdot \overline{x_i} + b ) -1]

최대 최소등 극점을 알아야 하므로 각각의 변수에 따른 편미분을 진행한다.

∂L∂W=w‾−∑αiyi⋅xi‾=0→w‾=∑αiyi⋅xi‾{\partial L\above{1pt}\partial W} = \overline w - \sum\alpha_iy_i \cdot \overline{x_i} = 0 \rightarrow \overline w = \sum\alpha_iy_i \cdot \overline{x_i}
∂L∂b=∑αiyi=0{\partial L\above{1pt}\partial b} = \sum\alpha_iy_i = 0

w‾\overline w은 몇몇 샘플들의 선형 결합으로 이루어짐을 알 수가 있다. α\alpha가 0인 경우를 제외하고 말이다. 이제 구한 ww를 위에서 정의한 간단한 식에 대입을 해보자.

L=12(∑αiyi⋅xi‾)(∑αjyj⋅xj‾)−(∑αiyi⋅xi‾)(∑αjyj⋅xj‾)−∑αiyib+∑αi=∑αi−∑i∑jαiαjyiyjxixjL = {1\above {1pt}2}(\sum\alpha_iy_i \cdot \overline{x_i})(\sum\alpha_jy_j \cdot \overline{x_j})-(\sum\alpha_iy_i \cdot \overline{x_i})(\sum\alpha_jy_j \cdot \overline{x_j})- \sum\alpha_iy_ib +\sum\alpha_i \\=\sum\alpha_i - \sum_i\sum_j\alpha_i\alpha_jy_iy_jx_ix_j

위 식을 통해 α\alpha를 구하게 되면 w‾\overline w 와bb를 구할 수 있게 되고 이를 통해 xx가 supportvectorsupport vector라 정의할 수 있다. SVM은 신경망과는 달리 localminimalocal minima에 빠질 걱정을 안해도 되는 것이 특징이다.

profile
Hun
이전 포스트

AutoEncoder(오토인코더)

0개의 댓글