Homogeneous Coordinates(동차좌표계)

참고자료

https://darkpgmr.tistory.com/78
https://www.youtube.com/watch?v=N6vP0T1Xabg&list=PLoJdZ7VvEiRNQwM3pcwHWwLQutIYMs4KK&index=1
https://gaussian37.github.io/vision-concept-homogeneous_coordinate/

---

Homogeneous Coordinates란?

그래픽스 또는 3D 비전 분야에서 많이 사용되는 좌표계이다. Homogeneous 좌표계를 사용하면 affine 변환과 perspective 변환이 하나의 행렬로 정의 된다. 예를 들어, (x, y)를 (x, y, 1)로 표현하는 것입니다.

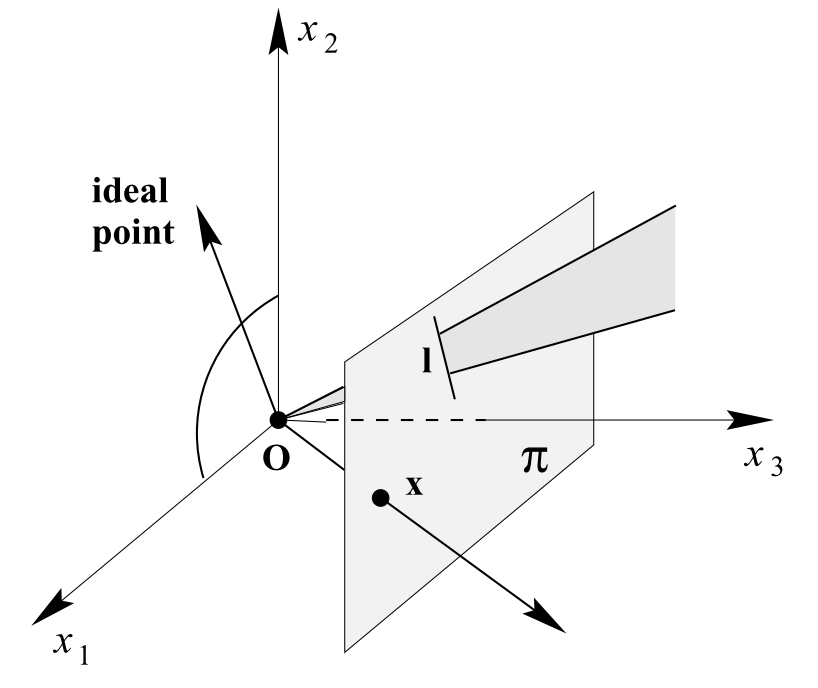출처 : https://gaussian37.github.io/vision-concept-homogeneous_coordinate/

선의 homogeneous coordinate 표현

직선의 방정식 ax + by + c = 0 을 ax + by + cw = 0로 표현 된다.
이때 ax + by + c = 0 상의 점으로 투영되는 점$(x, y, w)$들은 ax + by + cw = 0을 만족해야 한다.

점의 homogeneous coordinate 표현

임의의 0이 아닌 상수 $w$에 대해 점 $P(x,y)$의 좌표를 $P(wx, wy, w)$로 표현하는 방식이다. 2D 이미지에 한 점으로 투영 되는 모든 점(같은 ray 상의 점)들을 표현할 수 있다. 원래의 좌표를 구하고 싶다면 w = 1로 만들면 된다. $P(x, y, 1)$

점과 선의 관계

• $x = l\times l'$ -> 직선 $l$과 $l'$이 교차하는 점 $x$는 두 직선의 외적으로 구할 수 있다.
• $l = x \times x'$ -> 점 $x$와 $x'$를 이은 선 $l$은 두 점의 외적으로 구할 수 있다.
• 평행한 두 직선의 교차점은 무한대에 존재하고 이 교차점을 ideal point라 한다.
• 두 개의 ideal points를 연결한 직선을 ideal line이라 한다.
• $l \times l' =0$ -> 직선 $l$과 $l'$이 평행할 때 두 직선의 외적은 0이다.
  $Duality: x = l\times l' \leftrightarrow l=x\times x'$

Projective Transformation이란?

평면의 projective transformation

출처: https://medium.com/@unifyai/part-ii-projective-transformations-in-2d-2e99ac9c7e9f

• 선형변환을 수행하는 3X3 행렬로 수행한다.
• 평면 $\pi$를 $\pi'$로 변환하는 행렬 $H$라고 할 때 $x' = Hx이다.$
• 평면 위의 점 4개의 관계를 안다면 그 어떤 선형변환도 표현할 수 있다.
• 왜곡된 영상을 선형변환을 통해 보정할 수 있다.

출처: https://hopingtang.github.io/2016/06/13/notes-for-multiview-geometry-in-cv

결론은 Projective Transformation을 수월하게 하기 위해 Homogeneous Coordinates를 사용한다.