Epipolar geometry(에피폴라 기하학)

Hun·2023년 5월 18일

참고자료

https://www.youtube.com/watch?v=hdbv1FWOclc&t=80s
https://darkpgmr.tistory.com/83
https://darkpgmr.tistory.com/78

Epipolar geometry란?

스테레오 비전(stereo vision, 2-view)에서의 기하를 일컫는다. 동일한 사물/사람 장면을 서로 다른 두 지점에서 획득했을 때 매칭 쌍 $(m,m')$ 들 사이의 기하학적 관계를 다룬다.

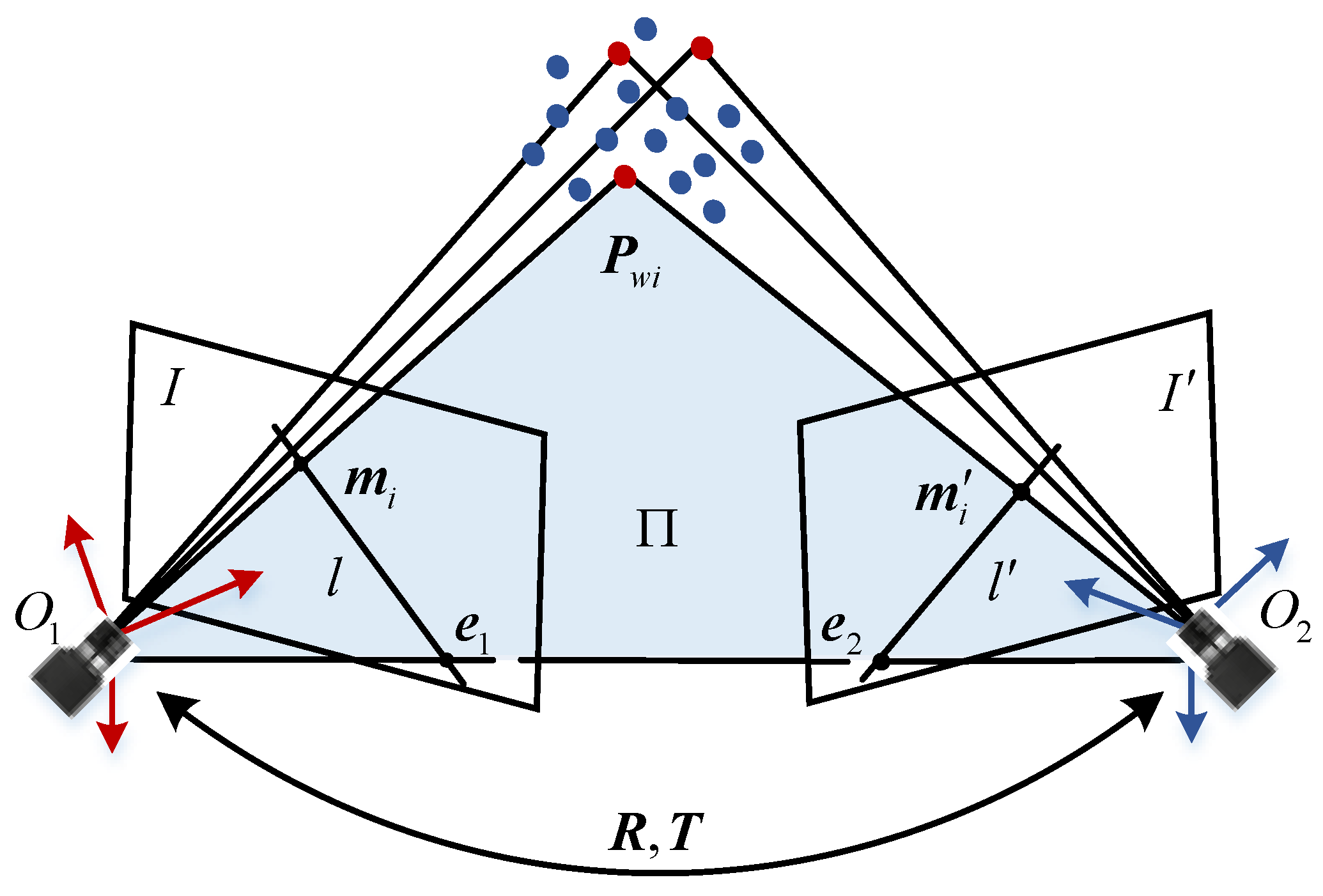에피폴라 기하학 구조 출처: A Global Fundamental Matrix Estimation Method of Planar Motion Based on Inlier Updating(논문)

용어정리

$P(P')$ : 이미지 상에 맺힐 3차원 공간상의 점

$O_1,O_2$ : 각 영상의 카메라 센터

$m,m'$ : 각 영상에서의 매칭쌍

$e, e'$ : epipole, 반대 영상의 카메라 센터가 해당 영상의 이미지 상에 맺힌 점 혹은 두 카메라 원점을 잇는 선과 이미지 평면이 만나는 점

$l, l'$ : epipolar line, 각 영상에서 epipole( $e,e'$ )과 이미지 상의 점( $m,m'$ )을 이은 선

기본 개념

두 카메라 위치 사이의 기하학적 관계 [R|T]를 알고 있고 영상 1에서의 영상좌표 m을 알고 있을 때, 점 P까지의 depth정보를 모른다면 영상좌표 $m$ 으로부터 투영되기 전의 3차원 좌표 P를 복원할 수 없다. 그러므로 점 P가 영상 2에 투영된 좌표 $m'$ 또한 유일하게 결정할 수 없다. 반면, P는 $O_1$ 와 $m$ 을 잇는 직선(ray)상에 존재하므로, 이 선이 반대 영상에 투영된 $l'$ 은 유일하게 존재한다. 이때, 1영상에서 2영상으로 대응되는 epipolarline( $l'$ )의 관계를 나타내는 행렬이 F, E(Fundamental, Essential)행렬이다. E, F 행렬은 두 이미지의 매칭쌍으로 카메라 이동행렬의 관계[R|T]를 정의한다. 이때, epipolar line을 이용한 제약식을 epipolar constraint 라고 한다.

E(Essential Matrix)

정규화된 이미지 평면에서의 매칭쌍들 사이의 기하학적 관계를 설명하는 행렬
3D 공간상의 한 점 P가 영상 1에서는 $m$ 에 투영되고, 영상 2에서는 $m'$ 에 투영됐다고 하면 아래 관계를 만족하는 행렬이 항상 존재한다는 것이 epipolar geometry의 핵심이다.