예전에 군대에 있을 때 블로그에 꽤나 기록을 했었는데, 기록을 한게 많이 부족하다고 생각해서 적었던 글을 다 삭제하였었다. 지금 생각해보면 남겨둘 걸이라고 아쉬움이 남기는 한다. 이번 기회에 딥러닝을 배울 기회가 생겨서 하는 김에 이번에는 제대로 블로그에 공부한 내용을 기록을 하려고 한다.
위에 보이는 서적은 라이브러리나 프레임워크에 의존하지 않고, 딥러닝의 핵심을 '밑바닥부터' 직접 만들어보며 즐거게 배울 수 있는 딥러닝 입문서라고 한다.
교수님께서 추천해주신 책이고, 평소에 딥러닝에 관심은 있었으나, 잘 몰랐기에 이번 기회에 블로그에 책의 내용을 정리하면서 배워보자.

하기에 앞서 Chapter1은 책에 대한 간략한 소개와 파이썬에 대한 소개이므로 생략을 하고 Chpater 2부터 하려고 한다.

Chapter 2

퍼셉트론(Perceptron)이란?

2장은 퍼셉트론에 대한 설명이다. 퍼셉트론의 유래는 Frank Rosenblatt 라는 인물이 1957년에 고안한 알고리즘이다.
딥러닝의 기원이 되는 알고리즘이기 때문에 책의 저자는 가장 첫 번째로 퍼셉트론을 먼저 언급한 것 같다.
먼저 정의를 한번 알아보자

퍼셉트론 : 다수의 신호를 입력으로 받아 하나의 신호를 출력한다.

여기서 말하는 신호는 전류나 강물처럼 흐름이 있는 것을 상상하면 좋다. 퍼셉트론 신호도 흐름을 만들고 정보를 앞으로 전달한다.
실제 전류와 달리 퍼셉트론 신호는 0 / 1 두개의 값만을 가진다.

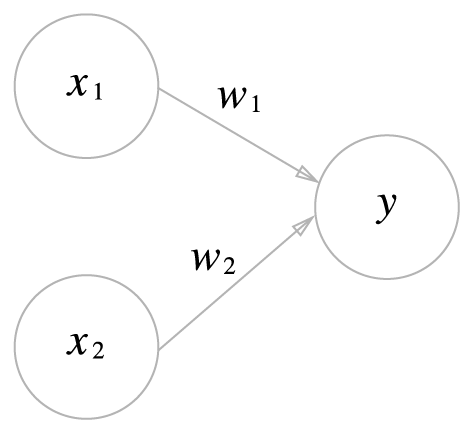
위의 사진은 입력이 2개인 퍼셉트론을 나타낸다. 원을 뉴런 혹은 노드라고 부른다. w 는 가중치(weight), x는 입력 신호이다.
뉴런에서 보내온 신호의 총합이 정해진 한계를 넘어설 때 1을 출력한다.그 임계값을 𝞱 라 한다.

여기서 𝞱를 -b 로 치환하면
b를 편향이라고 한다.

퍼셉트론의 한계

단층 퍼셉트론으로는 선형성을 가지고 있어, AND, OR, NAND 게이트는 표현할 수 있으나, XOR 게이트는 표현하지 못하게 된다.
이것을 해결하기 위해 다음 포스팅에서 얘기 할 다층 퍼셉트론이 나오게 된다. 다층 퍼셉트론으로는 비선형 영역도 표현을 할 수 있게 된다.