TIL_200908(Tree) Part 1

부트캠프 이머시브 9일차 TIL입니다.

오늘은 Tree와 Time Complexity에 대한 개념을 공부하고 직접 구현을 해보면서 배운 내용들을 정리 해보았습니다.

1. Tree에 대한 정리

1) Tree의 기본 개념 정리

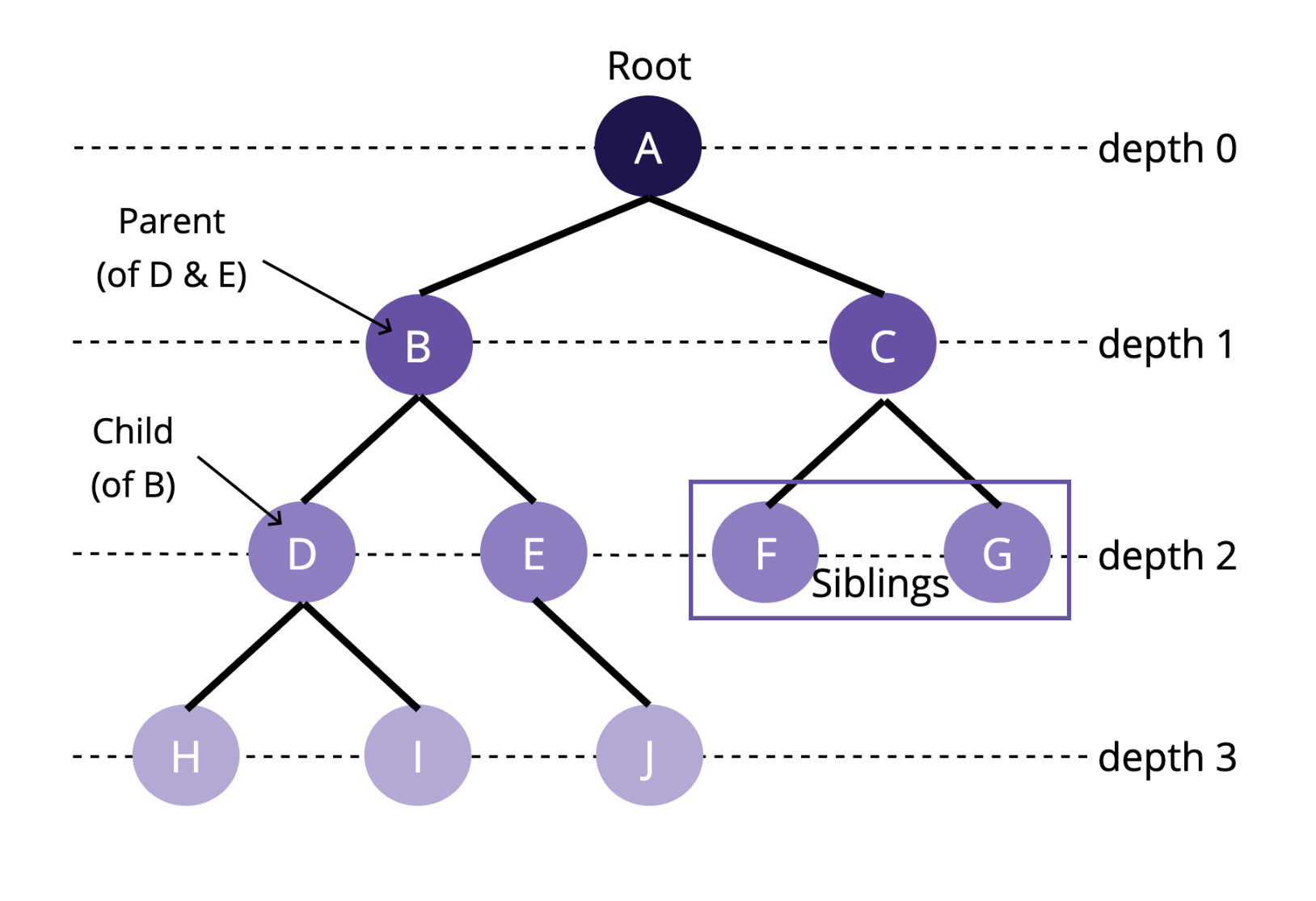
• Tree는 Node로 구성된 계층적 Data Structure임
• Node : 위 예시에서 A, B, C 등과 같이 트리의 구성요소임
• Root : A와 같이 최상단에 있는 노드임
• Depth : Root를 기준으로 다른 노드와의 접근 거리임
• Sibling : 같은 부모를 가지면서 같은 Depth에 존재하는 노드들은 Sibling 관계라고 함
• 그림에서 A는 B와 C의 Parent Node이고, B와 C는 A의 Child Node임
• Edge : 노드와 노드를 잇는 선
• Leaf : 자식이 없는 노드

2) Tree Depth & Height & Properties

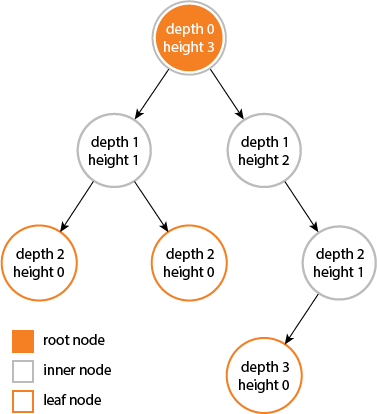
• Depth는 특정 노드에서 해당 Tree의 Root Node까지의 Edge갯수임
• Root Node의 Depth는 0임
• Height은 특정 노드에서 Leaf 노드까지 가장 긴 거리(Edge 갯수)임
• Tree의 Height은 Root Node의 Height 혹은 "Deepest Node"의 Depth와 같음
• Tree의 Diameter는 2개의 Leat Node간의 가장 긴 거리(Node의 갯수로서), 위 예시에서의 Tree의 Diameter는 6이라고 할 수 있음(각 Leaf Node도 Node의 갯수에 포함)

3) Tree와 Graph의 차이는?

• 그래프

  • 2개 이상의 경로가 가능하며, 노드들 사이에 무방향/방향에서 양방향 경로를 가질 수 있음
  • Self-loop뿐 아니라 Loop/Circuit도 가능
  • Root Node, Parent-Child Node 개념이 없음
  • 그래프의 순회는 Deep-Fist Search나 Breadth-First-Search로 진행
  • 그래프는 Cyclic 혹은 Acyclic || 방향 혹은 무방향 그래프로 구분할 수 있음
  • 간선의 유무는 그래프에 따라 다름
  • 그래프는 네트워크 모델임

• 트리

  • 트리는 그래프의 한 종류라고 할 수 있으며 "최소 연결 트리"라고도 불리며, 두 개의 정점 사이에 반드시 1개만의 경로를 가짐
  • Loop/Circuit/Self-loop이 불가능함
  • 각 노드들은 부모-자식 관계이므로 top-bottom 혹은 bottom-top으로 이뤄짐
  • Tree의 순회는 Pre-order, In-order, post-order 방식이 있음
    • 전위 순회(Preorder Traversal) : 부모 -> 좌 -> 우
    • 중위 순회(Inorder Traversal) : 좌 -> 부모 -> 우
    • 후위 순회(Postorder Traversal) : 좌 -> 우 -> 부모
  • Tree는 DAG(Directed Acyclic Graph)의 한 종류임
  • 간선은 항상 정점의 개수 - 1 만큼 가짐
  • 트리는 계층 모델이며, 그 종류로 이진트리, 이진탐색트리, AVL 트리, 힙 등이 있음

4) Binary Search Tree에 대한 기본 개념 정리

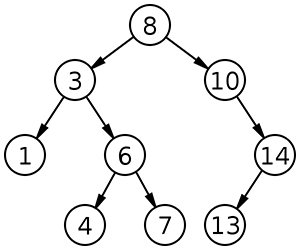
• 이진 탐색 트리는 각 노드별로 왼쪽 서브트리에 노드 값보다 작은 값을 가진 노드가, 오른쪽 서브트리에는 노드의 값보다 같거나 큰 값이 위치함
• 이진 탐색 트리는 최대 2개의 자식만 갖는 트리이며(눈치가 빠르다면 일반 트리는 2개 이상의 자식도 가질 수 있음을 알아야 함)
• 트리 구조는 재귀적이므로, 자식 노드 역시 최대 2개의 자식을 가질 수 있음

5) Binary Tree의 다른 종류들

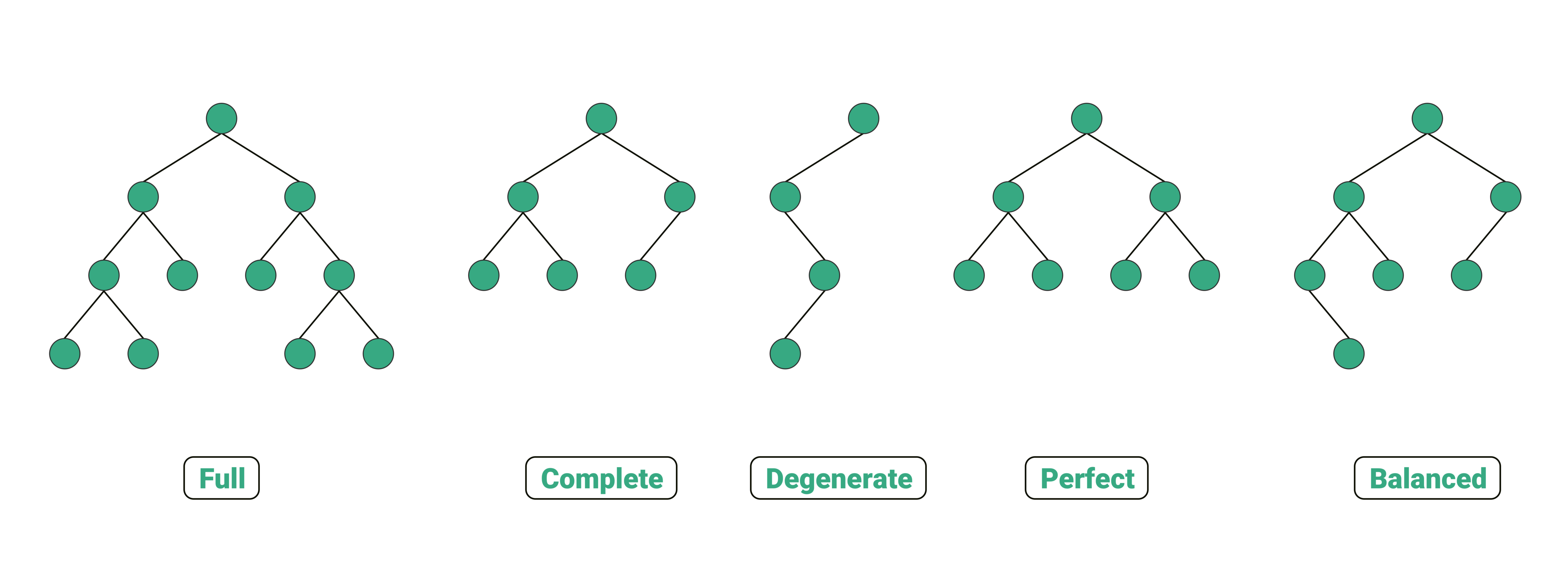
• 정 이진 트리(Full Binary Tree) : 모든 노드가 0 혹은 2개의 Child Node를 가진 Binary Tree(leaf node를 제외한 나머지 노드들이 2개의 children이 있다고 생각해도 됨)
• 완전 이진 트리(Complete Binary Tree) : A Binary Tree is a complete Binary Tree if all the levels are completely filled except possibly the last level and the last level has all keys as left as possible
• 포화 이진 트리(Perfect Binary Tree) : 모든 Internal Node가 2개의 children을 가지고 있고, 모든 leaf node가 같은 레벨에 있는 경우
• Balanced Binary Tree: n이 node의 갯수라고 한다면 Tree의 Height이 O(Log n)인 경우의 Binary Tree임
• Degenerate Tree: 모든 Internal Node가 1개의 child node만을 가진 경우를 말하며, 이 경우 performance 효율성은 Linked List와 동일하다고 보면 됨
• GeeksforGeeks 참조 링크