TIL_200907(Graph)

부트캠프 이머시브 8일차 TIL입니다.

오늘은 Graph에 대한 개념을 공부하고 직접 구현을 해보면서 배운 내용들을 정리 해보았습니다.

이번 TIL은 GeeksforGeeks 자료들을 참조하여 작성하였습니다.

---

1. Graph에 대한 정리

1) Graph의 기본 개념 정리

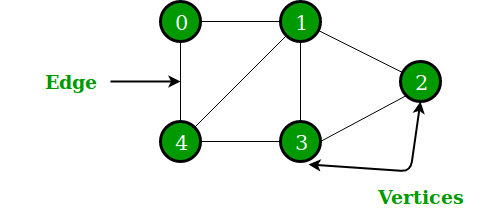
• Graph란 Vertex(정점)와 Edge(간선)로 구성된 한정된 자료구조임
• Vertex(정점)는 Node(노드)라고도 불리며, 위 예시에서는 "0", "1", "2", "3", "4" 등이 각각의 Node라고 할 수 있음.
• 위 노드들을 연결하는 선이 Edge임
• Graph는 무방향일 수 있는데, 이는 간선에 의해 연결된 2개의 노드가 대칭일 수 있다는 의미임
• Graph는 방향성을 가질 수도 있는데, 이는 비대칭 관계를 의미함
• Graph는 페이스북과 같은 SNS에서도 자주 이용되는 자료구조인데, 각각의 유저가 Node라고 한다면, 각 Node는 해당 유저의 ID, 성명, 젠더, 주거지 위치 등의 정보를 담고 있다고 생각하면 됨

2) 진입차수, 진출 차수에 대한 정리

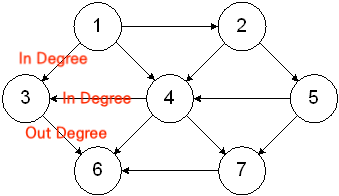
• 진입차수(In Degree)란 특정 Node로 갈 수 있는 간선의 수를 의미
• 진출 차수(Out Degree)란 특정 정점에서 갈 수 있는 간선의 수를 의미
• 위 예시의 경우 3번 노드로 들어오는 간선이 2개(In Degree는 2개)이고, 3번에서 6번 노드로 가는 간선 1개(Out Degree는 1개)임

3) 인접행렬(Adjacency Matrix)

다음과 같이 Graph가 있다고 가정해보겠습니다.

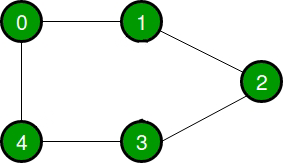
Graph를 구현할 때는 주로 인접행렬(Adjacency Matrix) 또는 인접 리스트(Adjacency List)를 활용한다고 하는데요.

먼저 인접 행렬에 대해서 살펴보겠습니다.

3-1) 인접 행렬에 대한 개념 정리

• 인접 행렬(Adjacency Matrix)이란 Vertex의 숫자인 V * V의 사이즈를 가진 2D Array임
• 2D Array는 adj[][]로 표현한다고 하면, adj[i][j]가 1일 경우 vertex i에서 vertex j 사이에 간선이 있다는 의미임
• 무방향 그래프를 구현한 인접 행렬의 경우 항상 두 노드는 대치형임
• 인접 행렬은 Weighted Graph를 구현할 때도 활용되며, adj[i][j] = w라고 할 때, vertex i와 vertex j 사이에 간선이 존재하며, 가중치는 w라는 의미임

3-2) 인접행렬의 시간/공간 복잡도

• 공간복잡도 : O(V^2)
  • 2D로 구현하면서 V * V 만큼의 공간이 소요 됨
• Vertex 추가(삭제) : O(V^2)
  • 새로운 Vertex를 추가하려면 저장 공간은 (V+1)^2으로 상승하기 때문에, 만일 공간을 늘리려면 전체 Matrix를 가져와야 하기 때문에 O(V^2)의 시간복잡도가 발생
• 간선 추가(삭제) : O(1)
  • matrix[i][j]의 값을 0에서 1로 수정하면 되기 때문에 시간 복잡도는 1임
• Querying(조회): O(1)
  • Vertex i와 Vertex j의 Index를 안 다면 시간 복잡도는 1이라고 할 수 있음

4) 인접 리스트(Adjacency List)

4-1) 인접 리스트에 대한 개념 정리

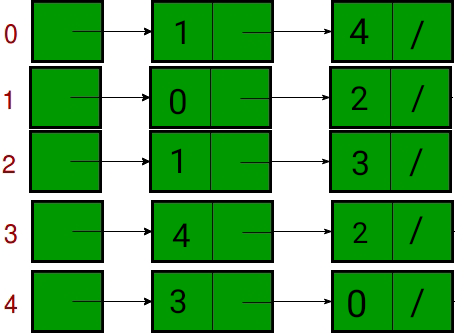
• 인접 리스트는 Linked List의 위치값으로 구성된 배열임
• Linked List의 첫 번째 Node는 Vertex라고 할 수 있고, 해당 노드에 연결된 나머지 노드들은 해당 노드와 연결된 다른 노드들이라고 할 수 있음
• 인접 리스트는 Weighted Graph를 구현할 때도 활용이 되는데, 각 간선의 가중치값을 저장하기 위해 Linked List에 일부 변화가 있을 수 있음.
• 그래프 예시와 비교를 해보면, 0번 Node는 1&4번 Node와 연결이 되었다는 것을 알 수 있는데, 인접 리스트에서도 마찬가지로 0번 Node와 1&4번 노드가 연결된 것을 확인할 수 있음.

4-2) 인접 리스트의 시간/공간 복잡도

• 공간복잡도 : O(V + E)
  • 전체 Vortex의 갯수 + 간선의 갯수를 구하면 됨
• Vertex 추가 : O(1)
  • 그냥 위 배열에 Vertex 한개를 추가하면 됨
• Edge 추가 : O(1)
  • Linked List에서 Edge만 추가하면 되기 때문에 O(1)임
• Vertex 삭제 : O(V + E)
  • 최악의 경우 모든 Vertex와 Edge를 조회한 후 삭제를 해야 할 수 있기 때문에 V + E임
• Edge 삭제 : O(E)
  • 최악의 경우 모든 Edge를 순회해야 할 수도 있기 때문에 Edge의 갯수임
• Querying(조회): O(V)
  • 최악의 경우 각각의 Vertex를 확인해야 하는 경우가 있기 때문에 Vertex의 갯수만금 Querying을 해야 함