[Algorithm] Dijkstra Alogorithm

Teddy_sh·2025년 8월 5일
Javaalgorithm

Algorithm

목록 보기
8/12
post-thumbnail

싸피에서 초반에 알고리즘 공부를 하며 내가 부족한 부분을 열심히 채우고있다. 어려운 알고리즘은 최대한 더 기억에 남고 응용할 수 있도록 기록을 해보려고한다.

추가적으로 나만의 알고리즘 학습법은 나는 어떤 알고리즘을 풀때 아예 그 유형의 기본적인 알고리즘 틀을 기본적으로 기억을 해두려고한다. BFS, DFS, TwoPointer 등 유형처럼 이미 틀이 정해져있는 알고리즘들은 거의 문제가 틀이 비슷하고 약간의 변형 응용같아서 이런식으로 진행해볼 예정이다.

다익스트라 알고리즘 (최단경로)

  • 시간 복잡도 : O(ElogV)
  • 한 시작점에서 모든 다른 정점까지의 최단거리를 구하는 그리디 알고리즘
    - 즉, 기본적으로 그리디 알고리즘이자, 다이나믹 프로그래밍 기법을 사용한 알고리즘이다.
  • 가중치 그래프 상에서 출발 노드에서 목표 노드까지 이동하는 가장 짧은 경로를 찾는 방법을 찾는다.
  • 하나의 출발 노드에서 다른 모든 노드로의 최단경로를 구할 수 있따.
  • 간선은 모두 양수여야한다.

다익스트라 알고리즘 동작 원리

1. 인접 리스트로 그래프를 구현한다.

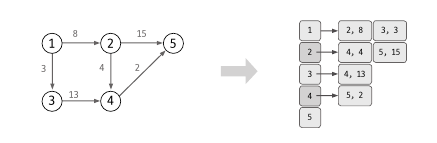
아래와 같이 Edge클래스를 만들어서 Edge형 ArrayList<>배열을 선언하여 구성한다.

ArrayList<Edge>[] graph;

class Edge{
	int targetNode; // 목표로 하는 노드.
    int weight; // 다음 노드로 가는데 필요한 비용 즉, 간선의 길이?
    public Edge(int targetNode, int wegith) {
    this.targetNode = targetNode;
    this.weight = weight;

2. 최단거리 배열 초기화 하기

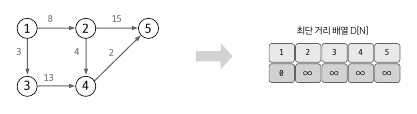
최단거리를 저장할 배열을 만들고, 출발 노드는0, 이외의 노드는 큰값 (Integer.MAX_VALUE)로 초기화한다.
노도 개수 +1의 배열을 만들어서 0번 인덱스를 사용하지 않는 방법을 이용하면 좋다.

int[] distance = new int[V + 1]; // V : 노드 개수
for(int i = 1 ; i <= V; i++ ){
	distance[i] = Integer.MAX_VALUE; // -> 모든 노드는 최대값으로 초기화
}

3. 현재 값이 가장 작은 노드를 고른다.

최단거리 배열에서 현재 값이 가장 작은 노드를 골라서 업데이트를 시작한다.

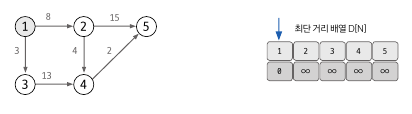
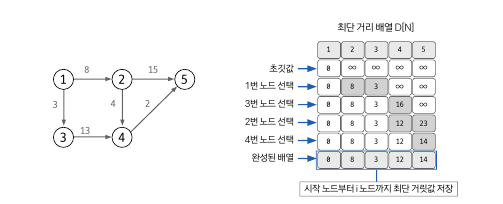
4. 최단거리 배열 업데이트

선택한 노드에 연결된 에지 값을 바탕으로 다른 노드의 최단거리 배열을 업데이트 한다.

현재 연결된 에지들은 모두 탐색하며, 최단거리 배열을 기존 값과 새로운 값중 더 작은 값으로 업데이트 한다.

if(distance[목표 노드] > distance[이전 노드] + 가중치 {
	distance[목표 노드] = distance[이전 노드] + 가중치;
}

5. 과정 3~4를 반복해서 최단거리 배열을 완성한다.

BOJ_1446 지름길

시행착오

  • 우선 우선순위 큐를 이용해서 가장 시간이 적게 걸리는 노드들을꺼내서 가장 짧은거리를 꺼내보도록 해보겠다.
  1. 우선순위큐 Node 클래스 삽입시 오류
  • 아래처럼 코드를 우선 짜보았다. 다음 target과 weight를 넣는데 문제가 생겼다.
  • 우선순위 큐에 크기순서대로 값을 넣어야하는데 어떤 값을 기준으로 비교할 Comparator이 존재하지 않아서 문제가 발생했다.

import java.io.*;
import java.util.*;

public class Main {

	class Node {
		int target;
		int weight;

		Node(int target, int weight) {
			this.target = target;
			this.weight = weight;
		}
	}

	static int shortcut, length;
	static PriorityQueue<Node> pq = new PriorityQueue<Node>();

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();
		StringTokenizer st = new StringTokenizer(br.readLine());

		shortcut = Integer.parseInt(st.nextToken());
		length = Integer.parseInt(st.nextToken());

		st = new StringTokenizer(br.readLine());

		for (int i = 0; i < shortcut; i++) {
			int target = Integer.parseInt(st.nextToken());
			int weight = Integer.parseInt(st.nextToken());
			pq.add(new Node(target, weight));
		}

	}

}

  • 해결

  • 아래와 같이 노드 클래스에 Comparable 인터페이스를 구현하여 가중치가 작은 순서대로 저장되도록 설계를 했다. 이러면 이제 가중치를 기준으로 저장을 할 수 있다.

++) 추가적으로 Node 클래스를 static 형태로 선언해 주었다.

	static class Node implements Comparable<Node>{
		int target;
		int weight;

		Node(int target, int weight) {
			this.target = target;
			this.weight = weight;
		}

		@Override
		public int compareTo(Node o) {
			return this.weight - o.weight;
		}
	}
  1. 기본 배열 선언
  • 아래와 같이 기초 거리들을 일단 0번 빼고 모두 Max값으로 초기화를 해준다. 
static int[] dist;
dist = new int[length + 1]; // 총 거리만큼 거리 배열 선언해주고
Arrays.fill(dist, Integer.MAX_VALUE); // 모든 배열을 최대값으로 설정해준다.
dist[0] = 0; // 시작 노드는 0
  • 아래와 같이 정적배열과 동적배열을 같이 선언해주고 정적배열마다 동적배열을 하나씩 할당해주었다.
static List<Node>[] graph; // 정적배열속 동적배열
graph = new List[length + 1];
for (int i = 0; i <= length; i++) {
	graph[i] = new ArrayList<>();
}
  1. 다익스트라 구현

package practice;

import java.io.*;
import java.util.*;

public class Main {

	static class Node implements Comparable<Node> {
		int target;
		int weight;

		Node(int target, int weight) {
			this.target = target;
			this.weight = weight;
		}

		@Override
		public int compareTo(Node o) {
			return this.weight - o.weight;
		}
	}

	static int shortcut, length;
	static PriorityQueue<Node> pq = new PriorityQueue<Node>();
	static int[] dist;
	static List<Node>[] graph; // 정적배열속 동적배열

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();
		StringTokenizer st = new StringTokenizer(br.readLine());

		shortcut = Integer.parseInt(st.nextToken());
		length = Integer.parseInt(st.nextToken());

		dist = new int[length + 1]; // 총 거리만큼 거리 배열 선언해주고
		Arrays.fill(dist, Integer.MAX_VALUE); // 모든 배열을 최대값으로 설정해준다.
		dist[0] = 0; // 시작 노드는 0

		graph = new List[length + 1];
		for (int i = 0; i <= length; i++) {
			graph[i] = new ArrayList<>();
		}

		for (int i = 0; i < length; i++) {
			graph[i].add(new Node(i + 1, 1)); // 다음 노드로 갈때마다 비용 1씩증가
		}

		for (int i = 0; i < shortcut; i++) {
			st = new StringTokenizer(br.readLine());
			int start = Integer.parseInt(st.nextToken());
			int target = Integer.parseInt(st.nextToken());
			int weight = Integer.parseInt(st.nextToken());

			if (weight < (target - start) && target <= length) { // 가중치가 해당 구간보다 비용이 적게들고,
				// 목표가 길이보다 길면안되겠지? -> 150까지 길인데 151이면 넘치니까 안넣음!
				graph[start].add(new Node(target, weight)); // 해당 시작점부터 다음 노드까지 몇 비용만큼의 지름길인지를 저장해준다.
			}

		}
		dijkstra();
		System.out.println(dist[length]);

	}

	static void dijkstra() {
		pq.add(new Node(0, 0));

		while (!pq.isEmpty()) {
			Node temp = pq.poll();

			int tempTarget = temp.target;
			int tempWeigth = temp.weight;

			if (tempWeigth > dist[tempTarget]) {
				continue;
			}

			for (Node next : graph[tempTarget]) {
				int newWeight = dist[tempTarget] + next.weight;
				if (newWeight < dist[next.target]) {
					dist[next.target] = newWeight;
					pq.add(new Node(next.target, newWeight));
				}
			}
		}
	}

}

SWEA 보급로 ( BFS + 다익스트라) 문제 이해를 위해 한 문제 더 해결하였습니다.

import java.io.*;
import java.util.*;
 
public class Solution {
 
    static int TC, N, ans;
    static int[][] map;
    static int[][] dist;
 
    static int[] dx = { 1, -1, 0, 0 };
    static int[] dy = { 0, 0, 1, -1 };
 
    static class Node implements Comparable<Node> {
        int x, y, cost;
 
        Node(int x, int y, int cost) {
            this.x = x;
            this.y = y;
            this.cost = cost;
        }
 
        @Override
        public int compareTo(Node o) {
            // TODO Auto-generated method stub
            return this.cost - o.cost;
        }
 
    }
 
    public static void main(String args[]) throws Exception {
 
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
 
        TC = Integer.parseInt(br.readLine());
 
        for (int k = 1; k <= TC; k++) {
 
            N = Integer.parseInt(br.readLine());
 
            map = new int[N][N];
            dist = new int[N][N];
 
            for (int i = 0; i < N; i++) {
                String input = br.readLine();
                for (int j = 0; j < N; j++) {
                    map[i][j] = input.charAt(j) - '0';
                    dist[i][j] = Integer.MAX_VALUE;
                }
            }
         
 
            ans = solution();
 
            sb.append("#").append(k).append(" ").append(ans).append("\n");
        }
        System.out.println(sb);
    }
 
    static int solution() {
        PriorityQueue<Node> pq = new PriorityQueue<Node>();
 
        dist[0][0] = map[0][0];
        pq.add(new Node(0, 0, map[0][0]));
 
        while (!pq.isEmpty()) {
            Node temp = pq.poll();
 
            int curX = temp.x;
            int curY = temp.y;
            int curCost = temp.cost;
 
            if (curCost > dist[curX][curY]) {
                continue;
            }
 
            for (int i = 0; i < 4; i++) {
                int nx = curX + dx[i];
                int ny = curY + dy[i];
                if (nx >= 0 && ny >= 0 && nx < N && ny < N) {
 
                    int newCost = dist[curX][curY] + map[nx][ny];
                    if (dist[nx][ny] > newCost) {
                        dist[nx][ny] = newCost;
                        pq.add(new Node(nx, ny, newCost));
                    }
                }
            }
 
        }
 
        return dist[N - 1][N - 1];
    }
}
profile
Teddy_sh
헬짱이 되고싶은 개발자 :)
이전 포스트

[Algorithm] Floyd Warshall Algorithm

다음 포스트

[Algorithm] 위상 정렬

0개의 댓글