[Algorithm] 위상 정렬

위상 정렬(Topological Sort)

사이클이 없는 그래프에서 노드의 순서를 찾는 알고리즘

• 그래프 내의 노드들 간의 선후 관계를 결정하여, 어떤 작업들이 먼저 수행되어야 하는지 순서를 정하는 것이 목표이다.
• 작업의 선후 관계를 결정해야 하거나 특정 순서로 작업을 처리해야 하는 문제에서 사용된다.
• 즉! 그래프에서 순서라는 단어가 나온다면 충분히 위상정렬을 생각 할 수 있다!

특징

• 위상 정렬을 방향 그래프에서 사용된다. 노드들 간의 방향성이 있는 의존관계를 표현하기 위해서 위상 정렬을 수행하는 것,
• 그래프에 사이클이 없어야한다! -> 사이클 존재시 위상정렬 불가.
  - 반대로 이 점을 사용하면 위상정렬을 수행해서 사이클을 탐지 가능
• 위상정렬 결과는 항상 유일하지 않다..
• 시간 복잡도 : O(V+E) -> V는 그래프 노드의 수, E는 간선의 수

위상 정렬 구하는 과정

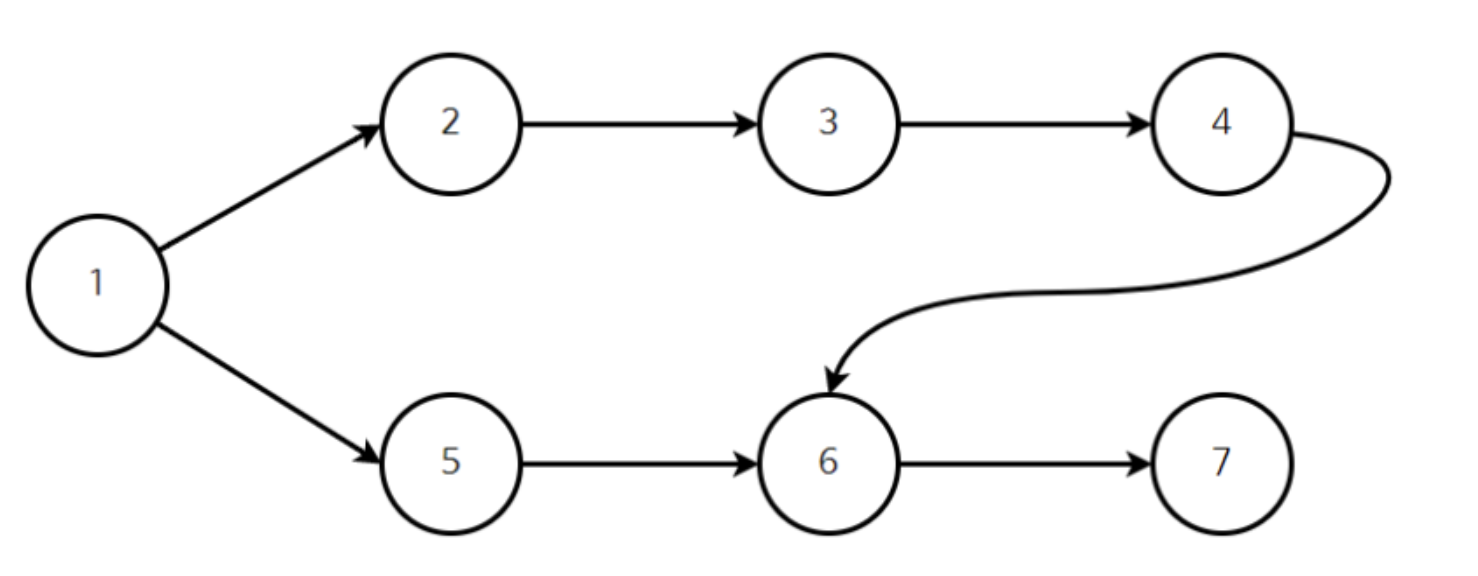
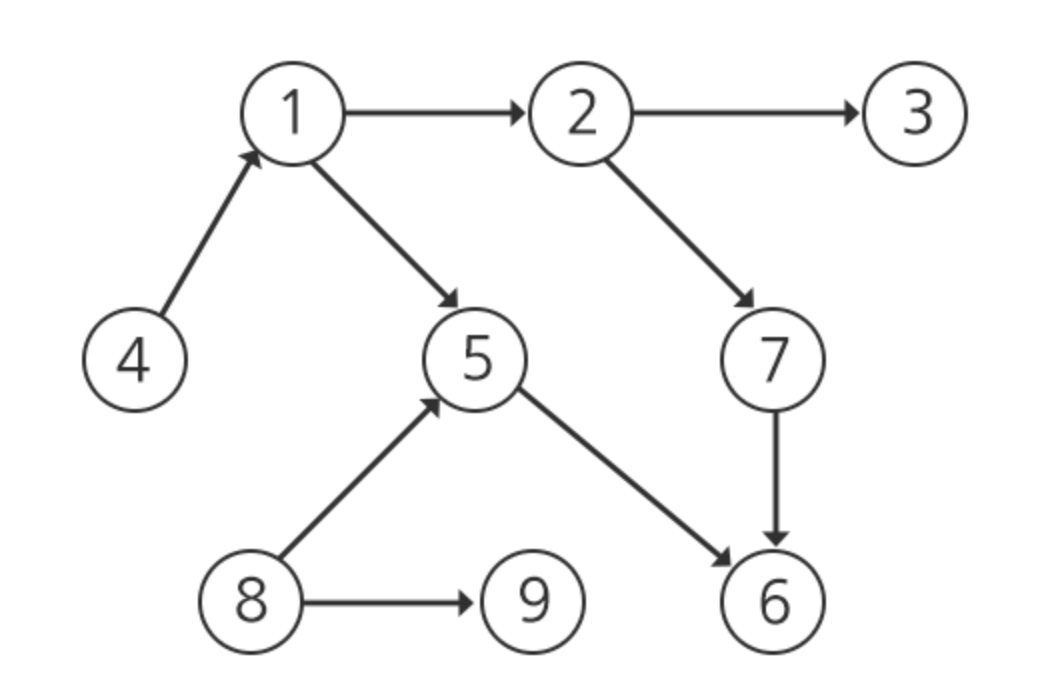
• 진입차수란? :부모노드의 개수 즉, 사진에서는 1번이 진입차수가 0이다. 2,5번은 1이고 6번 노드는 (5,4) 2개이다.

1. 진입 차수가 0인 정점을 큐에 삽입한다.
2. 큐에서 원소를 꺼내 연결된 모든 간선을 제거한다.
3. 간선 제거 이후에 진입차수가 0이 된 정점을 큐에 삽입한다.
4. 큐가 빌 때까지 2번~3번 과정을 반복한다. 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재하는 것이고, 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상 정렬의 결과이다.

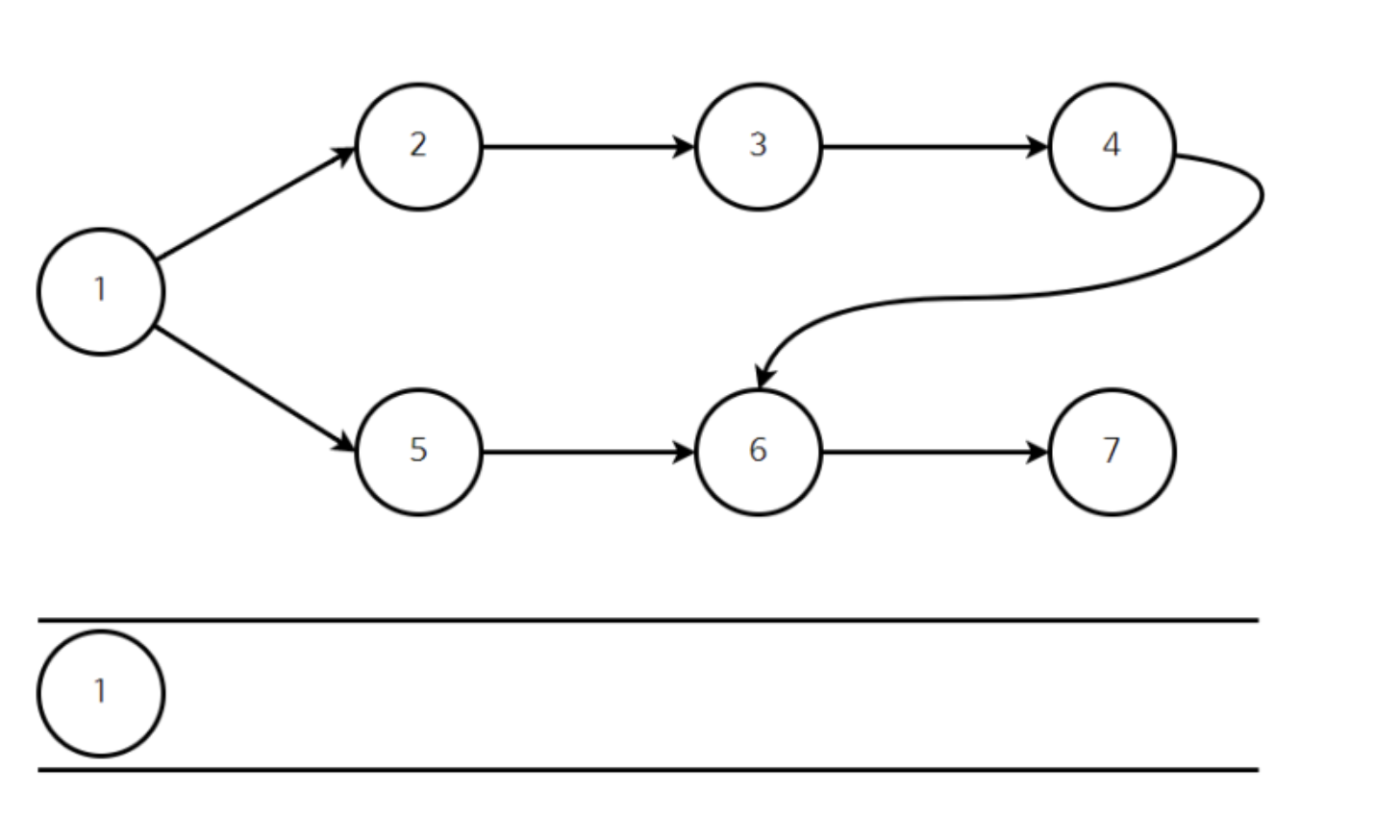
• 위와 같이 진입차수가 0인 정점 1을 큐에 삽입한다.

---

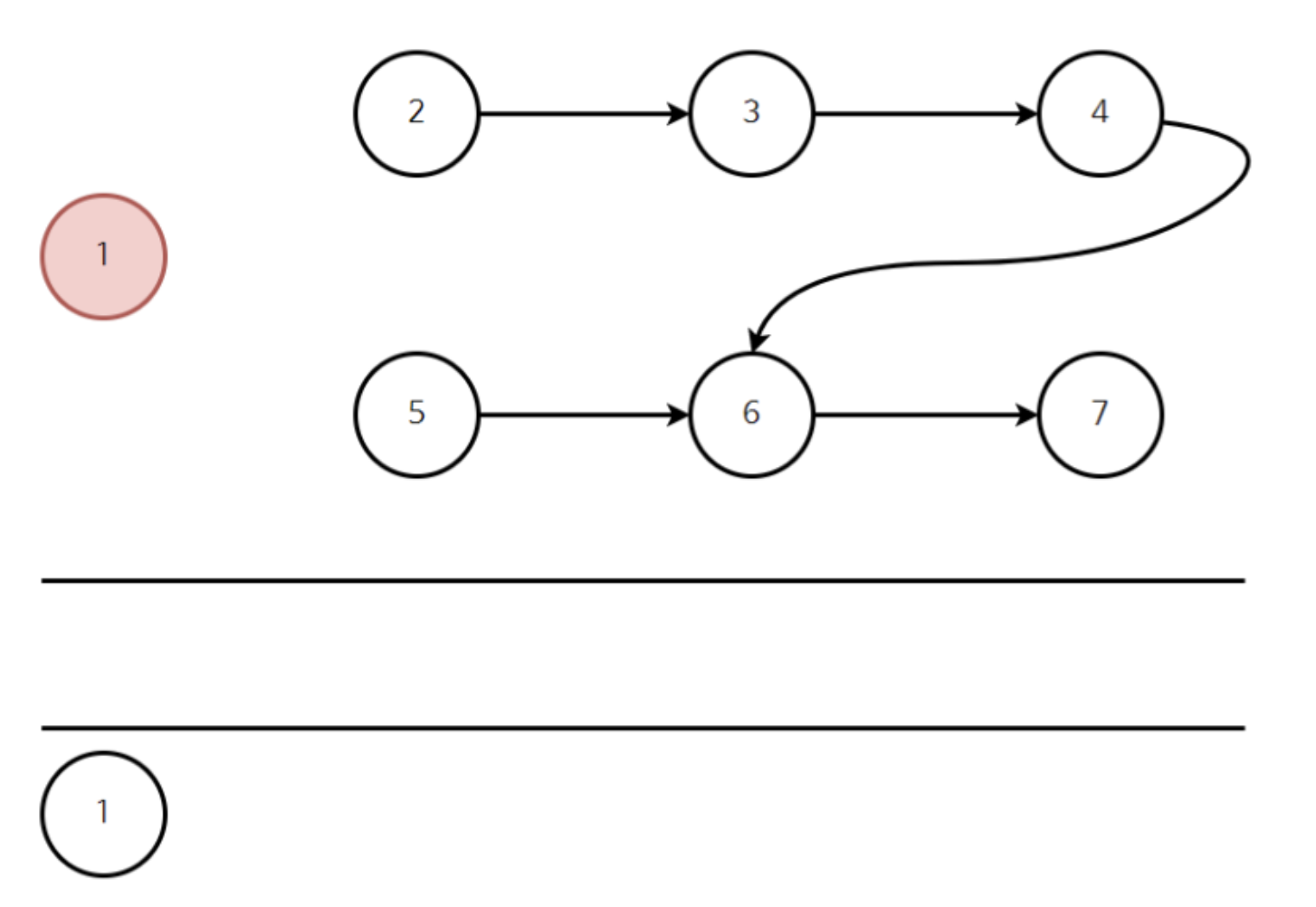
• 위와 같이 1을 큐에서 빼낸 뒤에 연결 되어있던 간선을 다 제거해준다.
  

---

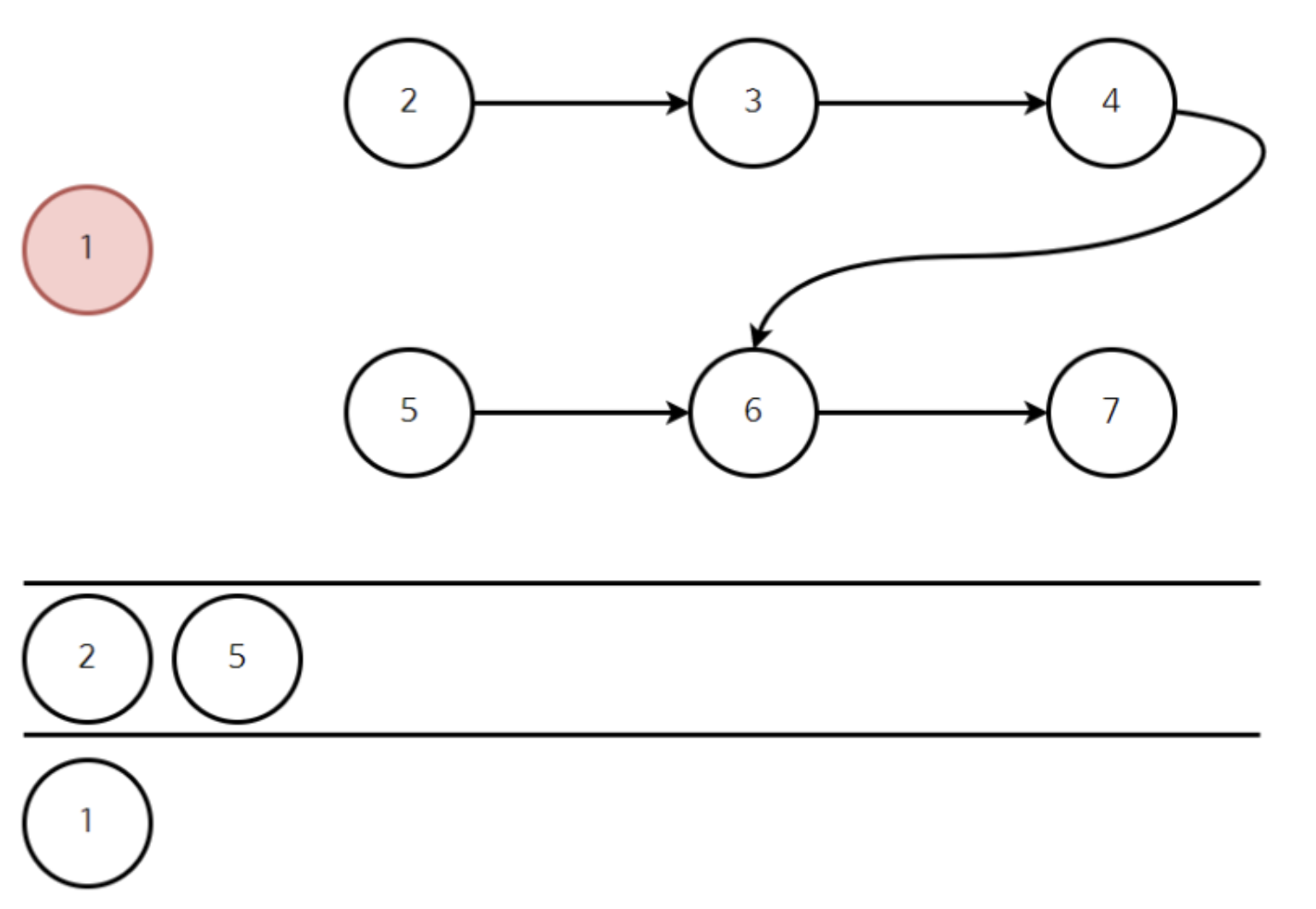
위처럼 이제 다시 큐에서 정점 2를 빼내주고 새롭게 3은 정점이 0이 될것이다. 이러한 과정을 반복해서 모두 큐에서 원소를 뺸 순서대로 나열한 것이 위상정렬이 된것이다.

• 이론적으로는 이해를 했으니 직접 문제를 풀며 코드를 작성해보겠습니다.

SWEA 작업순서 - D6

위 그래프 형태처럼 방향은 존재하고 사이클은 존재하지 않는 그래프를 위상정렬을 통해 값을 산출해내는 코드입니다.

import java.io.*;
import java.util.*;

public class SWEA_1267 {

	static int ans, V, E;
	static List<Integer>[] graph;
	static int[] inDegree;
	static List<Integer> result;

	public static void main(String[] args) throws Exception {

		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();

		for (int k = 1; k <= 10; k++) {

			StringTokenizer st = new StringTokenizer(br.readLine());
			V = Integer.parseInt(st.nextToken());
			E = Integer.parseInt(st.nextToken());

			graph = new ArrayList[V + 1];
			for (int i = 1; i <= V; i++) {
				graph[i] = new ArrayList<Integer>();
			}
			result = new ArrayList<Integer>();

			inDegree = new int[V + 1]; // 진입 차수 저장용
			st = new StringTokenizer(br.readLine());
			for (int i = 0; i < E ; i++) {

				int a = Integer.parseInt(st.nextToken());
				int b = Integer.parseInt(st.nextToken());
				graph[a].add(b);
				inDegree[b]++; // b에 들어오는 진입 차수가 추가되었으니 증가

			}

			topology();
			sb.append("#").append(k).append(" ");

			for (int i = 0; i < V; i++) {
				sb.append(result.get(i)).append(" ");
			}
			sb.append("\n");

		}
		System.out.println(sb);
	}

	static void topology() {

		Queue<Integer> q = new LinkedList<Integer>();

		for (int i = 1; i <= V; i++) {
			if (inDegree[i] == 0) {
				q.add(i); // 일단 진입차수 0인 애들 먼저 넣고
			}
		}

		while (!q.isEmpty()) {

			int temp = q.poll();
			result.add(temp);

			for (int i = 0; i < graph[temp].size(); i++) {
				inDegree[graph[temp].get(i)] -= 1; // 해당 노드랑 연결된 하위 노드들의 진입차수를 1 빼주고
				if (inDegree[graph[temp].get(i)] == 0) {
					q.add(graph[temp].get(i)); // 만약 진입차수 -1 했는데 0이면 q에 넣고
				}
			}

		}

	}

}