[Algorithm] 세그먼트트리

세그먼트 트리란

| 특정 구간 내 데이터에 대한 연산을 빠르게 구할 수 있는 트리,
| ex) 특정 구간 합, 최소값, 최대값, 평균 값 등...

시간 복잡도

• 데이터 변경 : O(logN)
• 연산 : O(logN)
• 데이터 변경할 때마다 M번 연산 : O((logN + logN)*M) = O(MlogN)

구조적 특징

• 완전 이진 트리 형태

• 각 노드는 특정 구간의 정보를 저장

• 리프 노드 : 원본 배열의 각 원소

• 내부 노드 : 자식 노드들의 정보를 합친 값
  

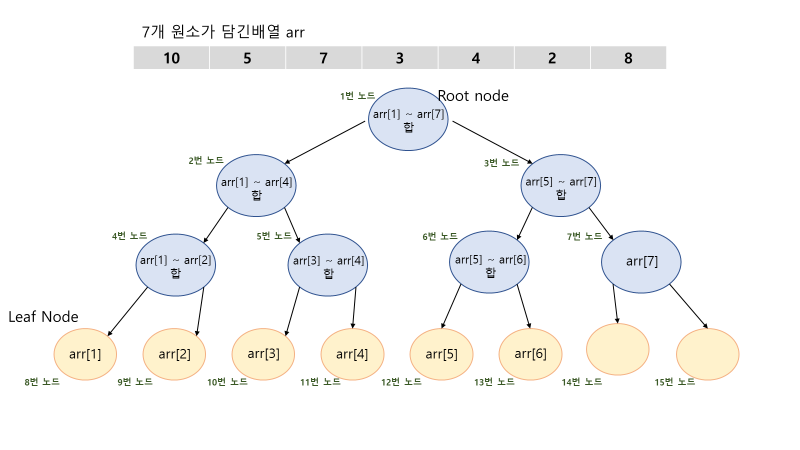
• 위 사진을 보면 우선 왼쪽 리프노드는 부모 노드의 번호의 2이다, 오른쪽 리프 노드는 부모 노드 번호의 2 +1 이다.

• 이를 통해서 해당 시작~ 해당 노드까지의 합, 해당 노드 ~ 끝 노드까지의 합을 구할 수 있다.

코드 구현

• 아래 코드는 트리를 구성하고, 구하고싶은 구간의 start, end를 입력하면 해당 구간의 합을 구하는 코드이다.

1. tree를 구성한다. build 배열을 통해 구성하는 것이다

• 우선 start == end라면 해당 노드의 값, 즉 arr[start] 를 반환하거나 end를 반환하면 된다.
• 아니라면 양쪽 구간합을 찾아와서 더해준것을 tree[node]에 넣어준다.

2. build를 통해 노드마다 구간합을 저장해 두었을 것이다.

• query를 통해 시작과 끝을 입력받고 모든 전체 구간에서 원하는 구간의 결과값을 찾으면 된다.
• 만약, 내가 찾는 right 값이 start보다 작다면, 혹은 left값이 end보다 크다면? 아예 겹치는 구간이 존재하지 않는것이다. 0을 반환한다.
• 만약, 내가 찾는 left값이 start보다 작거나 같고, end 값보다 right가 크다면 해당 구간합을 반환한다. -> 왜냐면 내가 찾는 구간의 사이에 껴있는 것이니까, 만약 일부만 겹친다면 해당 구간을 쪼개서 겹치는 부분만 반환한다!

public class SegmentTree {

	static long[] tree;
	static int N;

	public SegmentTree(int[] arr) {
		N = arr.length;
		tree = new long[4 * N];
		build(arr, 1, 0, N - 1);
	}

	// tree 배열을 구축
	private long build(int[] arr, int node, int start, int end) {
		if (start == end) {
			return tree[node] = arr[start];
		}

		int mid = (start + end) / 2;
		long leftSum = build(arr, node * 2, start, mid); // 왼쪽 합은 현재 노드의 번호 *2이며, 시작과 끝은 현재 위치부터 중간까지 
		long rightSum = build(arr, node * 2 + 1, mid + 1, end);
		return tree[node] = leftSum + rightSum; // 
	}

	public long query(int left, int right) {
		return query(1, 0, N - 1, left, right); // 모든 구간에서 / 찾는 구간 찾기,
	}

	private long query(int node, int start, int end, int left, int right) {
		if (right < start || end < left) { //  구간이 아예 안겹치는 경우 
			return 0;
		}
		
		if(left <= start && end <= right) { // 내가 찾는 구간이 start보다 작거나 같고, end보다 크거나 같으면 구간 일치, 그떄의 구간 합 반환 
			return tree[node];
		}

		int mid = (start + end) / 2;
		// 구간이 일부만 겹치면 양쪽자식을 탐색해서 얻어온다.
		long leftSum = query(node * 2, start, mid, left, right);
		long rightSum = query(node * 2 + 1, mid + 1, end, left, right);
		return leftSum + rightSum;

	}


	public static void main(String[] args) {
		int[] arr = { 75, 30, 100, 38, 50, 51, 52, 20, 81, 5 };
		SegmentTree seg = new SegmentTree(arr);

		System.out.println("구간 1 " + seg.query(1, 4));
		System.out.println("구간 2 " + seg.query(4, 8));

	}

}

---

백준 2357 최솟값, 최댓값 - 세그먼트 트리

• 이 문제에서는 똑같이 세그먼트 트리를 구현하고, 세그먼트 트리는 다양한 값들을 저장할 수 있다. 구간합, 최대 최소, GCD 등을 저장한다. 이 코드에서는 최대값, 최소값을 저장하는 코드이다.
• minTree, maxTree를 구성하고 세그먼트 로직 build를 할때 자식 노드중 가장 작은것들, 가장 큰것들을 갱신해주면서 트리를 구성해준다. 그리고 query문을 통해서 해당 내가 찾는 구간의 교집합들을 다 탐색하면서 그 구간의 가장 작은값, 큰값들을 갱신해주어 정답을 출력한다.
• 세그먼트 트리는 어려운 개념같다. 이번에 푸는걸로 만족하지 않고 이 게시물의 내용을 점차 늘려가보겠다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {

	static int[] minTree;
	static int[] maxTree;
	static int N;
	static int[] arr;

	Main(int[] arr) {
		N = arr.length - 1;
		minTree = new int[N * 4];
		maxTree = new int[N * 4];
		build(arr, 1, 1, N);

	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();
		StringTokenizer st = new StringTokenizer(br.readLine());

		int arrSize = Integer.parseInt(st.nextToken());
		int find_seg = Integer.parseInt(st.nextToken());

		arr = new int[arrSize + 1];

		for (int i = 1; i <= arrSize; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}

		Main seg = new Main(arr);
		for (int i = 0; i < find_seg; i++) {
			st = new StringTokenizer(br.readLine());
			int start = Integer.parseInt(st.nextToken());
			int end = Integer.parseInt(st.nextToken());

			sb.append(seg.queryMin(start, end)).append(" ").append(seg.queryMax(start, end)).append("\n");

		}
		System.out.println(sb);

	}

	public void build(int[] arr, int node, int start, int end) {
		if (start == end) {
			minTree[node] = arr[start];
			maxTree[node] = arr[start];
			return;
		}

		int mid = (start + end) / 2;
		build(arr, node * 2, start, mid);
		build(arr, node * 2 + 1, mid + 1, end);

		minTree[node] = Math.min(minTree[node * 2], minTree[node * 2 + 1]);
		maxTree[node] = Math.max(maxTree[node * 2], maxTree[node * 2 + 1]);
	}

	public int queryMin(int left, int right) {
		return queryMin(1, 1, N, left, right);
	}

	public int queryMax(int left, int right) {
		return queryMax(1, 1, N, left, right);
	}

	public int queryMin(int node, int start, int end, int left, int right) {
		if (end < left || right < start) {
			return Integer.MAX_VALUE;
		}

		if (left <= start && end <= right) { // 내가 찾는 구간사이에 start ~ end 가 있다면 반환,
			return minTree[node];
		}

		int mid = (start + end) / 2;
		int leftMin = queryMin(node * 2, start, mid, left, right);
		int rightMin = queryMin(node * 2 + 1, mid + 1, end, left, right);
		return Math.min(leftMin, rightMin);

	}

	public int queryMax(int node, int start, int end, int left, int right) {
		if (end < left || right < start) {
			return Integer.MIN_VALUE;
		}

		if (left <= start && end <= right) {
			return maxTree[node];
		}

		int mid = (start + end) / 2;
		int leftMax = queryMax(node * 2, start, mid, left, right);
		int rightMax = queryMax(node * 2 + 1, mid + 1, end, left, right);
		return Math.max(leftMax, rightMax);
	}

}