최소 신장 트리
- 그래프의 모든 정점을 사이클 없이 잇는(신장 트리)에서 간선의 가중치의 합이 최소가 되는 트리
-> 다익스트라는 해당 노드에서 다른 모든 정점까지의 최단거리를 구하는 것, MST는 A에서 목적지 B까지 가는 가중치의 값이 가장 작은 경로를 구하는 것
즉, 다익스트라는 모든 노드의 거리, MST는 A - B까지 하나의 경로
스패닝 트리 : 모든 노드는 연결되어 있지만, 사이클이 존재하지 않는 부분 그래프를 의미.
크루스칼 알고리즘이란?
- 간선 중심으로 최소 신장 트리를 구하는 알고리즘 ( 간선이 적을때는 크루스칼이 유리하다. )
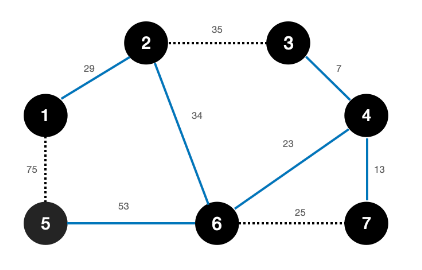
- 위와같은 그래프가 있다고 보자.
- 가장 간선의 가중치가 작은것부터 연결한다.
- 작은것부터 고르다가 만약 골랐을때 사이클이 발생한다면 고르지 않는다.
- union-find를 이용해서 만약 2개의 노드가 하나의 정점을 갖고있다면 -> 사이클이 발생 -> 합치지 않고 넘어간다.
아래 코드와 같이 정점이 같으면 false 아니라면 편향을 임시로 막기위해 더 find 값으로 노드를 합친다.
static boolean union(int x, int y) {
int nx = find(x);
int ny = find(y);
if (nx == ny)
return false;
if (nx > ny)
parent[ny] = nx;
else
parent[nx] = ny;
return true;
}
전체 코드를 통해 크루스칼 알고리즘을 알아보자
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
//신장 트리
//n개의 정점으로 이루어진 '무향' 그래프에서 n개의 정점과 n-1개의 간선으로 이루어진 트리
//최소 신장 트리
//무향 가중치 그래프에서 신장트리를 구성하는 간선들의 가중치의 합이 최소인 신장 트리
//------------
//KRUSKAL 알고리즘 -> Union-Find O(ElogE)
//간선을 하나씩 선택해서 MST를 찾는 알고리즘
//1. 최초, 모든 간선을 가중치에 따라 '오름차순'으로 정렬
//2. 가중치가 가장 낮은 간선부터 선택하면서 트리를 증가시킴
//3. n-1개의 간선이 선택될 때까지 2를 반복
//PRIM 알고리즘 -> 우선순위 큐 or 인접행렬 O(V^2) or O(ElogV)
//1. 임의의 시작 정점 선택
//현재 트리와 연결된 간선 중 최소 비용 간선 선택
//새로운 정점을 트리에 추가
//모든 정점이 포함될 때까지 반복
public class MST_KRUSKAL {
static class Edge implements Comparable<Edge> {
int from, to, weight;
public Edge(int from, int to, int weight) {
super();
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
// 10 - 20 : 음수 -> 뒤 값이 크다 : 그럼 그대로 위치 (교환 일어나지 않음)
// 20 - 10 : 양수 -> 앞 값이 크다 : 교환
return this.weight - o.weight; // 가중치 기준 오름차순 정렬 되도록 비교결과 리턴
// return Integer.compare(this.weight, o,weight); 간선에 음수값이 있을 수 있어서 이렇게도 가능
}
}
static Edge[] edgeList;
static int[] parent;
static int V, E;
public static void main(String[] args) throws Exception {
parent = new int[V];
for (int i = 1; i <= V; i++) {
parent[i] = i;
}
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
edgeList = new Edge[E];
for (int i = 0; i < E; i++) {
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
edgeList[i] = new Edge(from, to, weight);
}
Arrays.sort(edgeList);
int result = 0;
int cnt = 0;
for (Edge edge : edgeList) {
if (!union(edge.from, edge.to))
continue;
result += edge.weight;
if (++cnt == V - 1)
break;
}
System.out.println(result);
}
static boolean union(int x, int y) {
int nx = find(x);
int ny = find(y);
if (nx == ny)
return false;
if (nx > ny)
parent[ny] = nx;
else
parent[nx] = ny;
return true;
}
static int find(int x) {
if (x == parent[x]) {
return x;
}
return parent[x] = find(parent[x]);
}
}
- Edge클래스에다가 시작, 끝, 가중치를 담아준다. compare을 이용해서 가중치가 작은 순으로 저장을 해준다. 이때 꼭 Arrays.sort를 해서 가중치순으로 정렬을 해주자.
- union을 하며 union이 성공할때마다 해당 가중치를 정답에 더해주고, cnt를 증가시킨다.
- 만약 cnt 값이 정점 -1개만큼 되었다면, 모두 연결되었다는 뜻이고 종료하여 정답을 출력한다.
- 크루스칼 알고리즘은 Union-find 알고리즘을 이용해서 '간선'의 값을 기준으로 최소신장트리를 구성하는 그리디기반 알고리즘이다.
프림 알고리즘이란?
-
프림 알고리즘은 최소 신장트리를 구하는 또하나의 알고리즘이다. 하나의 시작 '정점'을 기준으로 가장 작은 간선과 연결된 정점을 선택하여 스패닝 트리가 될 때까지 모든 노드를 연결시킨다.
-
프림알고리즘은 간선의 개수가 많은 경우에는 정점 위주의 프림이 유리하다.
동작과정
- 임의의 간선을 선택.
- 선택한 간선의 정점으로부터 가장 낮은 가중치를 갖는 정점을 선택.
- 모든 정점에 대하여 2번의 과정을 반복한다.
import java.io.*;
import java.util.*;
//신장 트리
//n개의 정점으로 이루어진 '무향' 그래프에서 n개의 정점과 n-1개의 간선으로 이루어진 트리
//최소 신장 트리
//무향 가중치 그래프에서 신장트리를 구성하는 간선들의 가중치의 합이 최소인 신장 트리
//------------
//KRUSKAL 알고리즘 -> Union-Find O(ElogE)
//간선을 하나씩 선택해서 MST를 찾는 알고리즘
//1. 최초, 모든 간선을 가중치에 따라 '오름차순'으로 정렬
//2. 가중치가 가장 낮은 간선부터 선택하면서 트리를 증가시킴
//3. n-1개의 간선이 선택될 때까지 2를 반복
//PRIM 알고리즘 -> 우선순위 큐 or 인접행렬 O(V^2) or O(ElogV)
//1. 임의의 시작 정점 선택
//현재 트리와 연결된 간선 중 최소 비용 간선 선택
//새로운 정점을 트리에 추가
//모든 정점이 포함될 때까지 반복
public class MST_PRIM {
static int TC, V, E;
static long ans;
static List<Edge>[] adjList;
static boolean[] visited;
static class Edge implements Comparable<Edge> {
int to;
long weight;
Edge(int to, long weight) {
this.to = to;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
// TODO Auto-generated method stub
return Long.compare(this.weight, o.weight);
}
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
TC = Integer.parseInt(br.readLine());
for (int k = 1; k <= TC; k++) {
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
ans = 0;
visited = new boolean[V + 1];
adjList = new ArrayList[V + 1];
for (int i = 0; i < V + 1; i++) {
adjList[i] = new ArrayList<Edge>();
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
long weight = Integer.parseInt(st.nextToken());
adjList[from].add(new Edge(to, weight));
adjList[to].add(new Edge(from, weight));
}
prim(1);
sb.append("#").append(k).append(" ").append(ans).append("\n");
}
System.out.println(sb);
}
static void prim(int start) {
PriorityQueue<Edge> pq = new PriorityQueue<>();
pq.add(new Edge(start, 0));
while (!pq.isEmpty()) {
Edge edge = pq.poll();
int to = edge.to;
long weight = edge.weight;
if (visited[to])
continue;
visited[to] = true;
ans += weight;
for (Edge e : adjList[to]) {
if (!visited[e.to]) {
pq.add(new Edge(e.to, e.weight));
}
}
}
}
}
- 우선 정점을 방문했는지 체크하는 visited 배열을 선언해준다.
- Edge클래스는 해당 정점은 알고있으므로, 목적지와 가중치만을 갖고있는 Class를 선언해준다.
- 인접리스트를 선언하여 양방향 그래프로 이어준다.
- 우선순위큐를 선언해서 해당 노드부터 시작하여 다음 가중치의 값이 가장 작은것부터 이어주고 방문처리를 해준다.

