[1주차] Examples and Technologies of Censored Data

참고교재

• Groeneboom and Jongbloed (2014), Nonparametric Estimation under Shape Constraints, Cambridge University Press.
• Wooldridge (2010), Econometric Analysis of Cross Section and Panel Data, 2nd Edition, MIT Press.

참고자료

[Lecture Note] https://scholar.harvard.edu/files/montamat/files/nonparametric_estimation.pdf
[Github Docs] https://reliability.readthedocs.io/en/latest/What%20is%20censored%20data.html

 

1. Nonparametric Estimation

Nonparametric Estimation (비모수적 추정)이란 관측치의 분포 함수에 대한 최소한의 가정을 기반으로 분포 함수를 추정하는 방법이다. 관측치가 특정 분포를 따른다는 강력한 가정을 갖는 Parametric Estimation과 달리, 관측치의 분포에 대해 함부로 단정지을 수 없는 경우에 사용한다.

대표적인 Nonparametric Estimation의 예시로

• Kernel Estimation : Density Function의 각 함숫값을 결정할 때, 각 점의 local한 범위 내의 값이 전체 관측치에서 얼마나 관측되었는지 그 비율을 함숫값으로 결정하는 기법

이 있다. local한 범위 안에서 관측치가 중심점과 얼마나 멀리 있느냐에 따라 가중치를 부여하기도 하며, 관측치마다의 가중치를 계산하는 함수를 Kernel function이라 한다. 범위와 그에 따른 가중치를 어떻게 잡느냐에 따라 Uniform Kernel, Normal Kernel 등으로 세분화될 수 있다. 의미상으로는 Neural Network의 Kernel과 일맥상통하는 듯 하다.

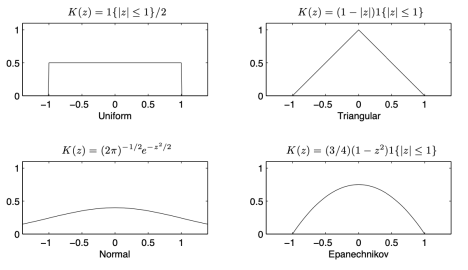
교재에 소개된 몇 가지 예시 상황을 살펴보자.

 

1.1 Is There a Warming-up of Lake Mendota?

Lake Mendota는 미국에 위치한 호수로, 1800년대부터 연구가 시작되어 오랜 기간 데이터를 축적한 좋은 샘플이다. 예시로 살펴볼 데이터는 1855년부터 157년간 측정한 Lake Mendota가 얼어있는 일 수이다.

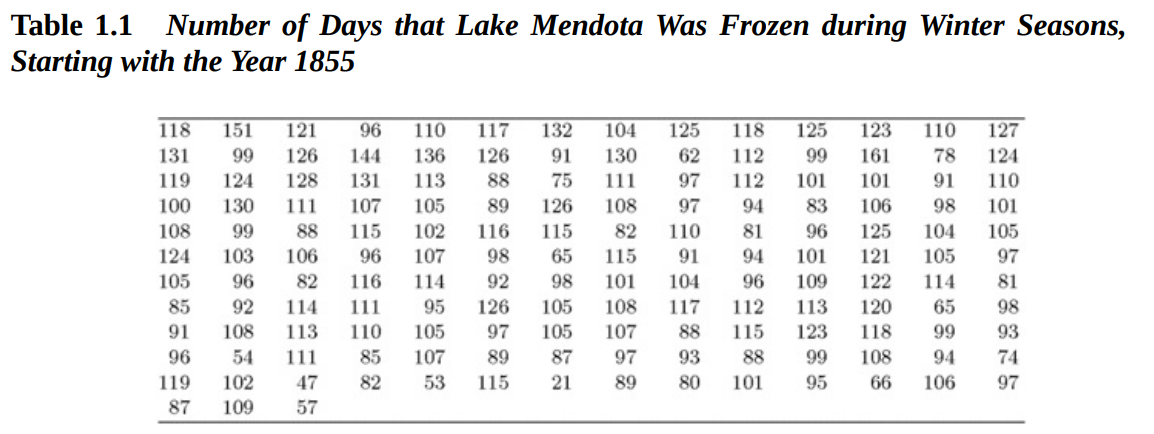
$i$의 증가를 연도의 증가(=시간의 흐름)로 볼 때, 호수가 얼어있는 일 수 $v_i$를 모델링하고자 한다. 이 때 호수가 얼어있는 일 수가 점점 짧아질 것이라고 가정하여 (혹은 선행 분석을 통해 감소추세임을 밝혀내어)

을 만족한다고 하자. 157년간 관측된 데이터를 $Y_i$라 할 때,

을 최소화하는 것이 목표가 되겠다. 이렇게 단조증가/단조감소하는 estimator를 Isotonic estimator라 하고, 이를 모델링하는 과정을 Isotonic regression이라 한다.

$v_i$를 추정하기 위한 실질적인 방법으로

의 (least) concave majorant의 left derivative를 활용할 수 있다.(이론적 근거는 2주차에 계속) 이로부터 추정한 $v_i$는 아래 (a)의 실선과 같고, 이를 smooth하게 이은 결과는 아래 (b)의 실선과 같다.

 

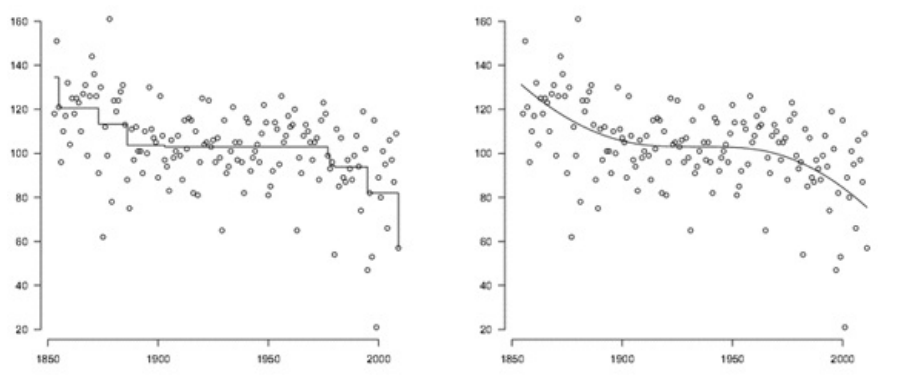
1.2 Onset of Nonlethal Lung Tumor

두 그룹의 쥐의 수명을 측정한 데이터를 살펴보자. 한 그룹은 무균 환경, 다른 한 그룹은 일반 환경에 놓여있으며, 관심분포는 RFM type의 폐 종양이 쥐에게 발병하는 나이이다.

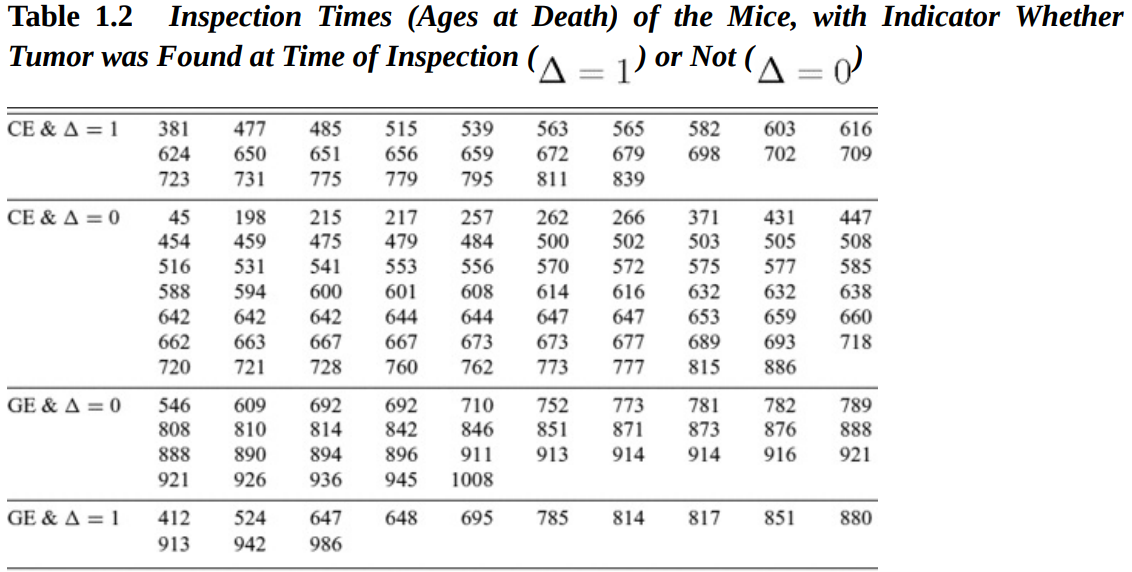
CE(=Conventional Environment, 일반 환경)과 GE(=Germ-free Environment, 무균 환경)에서 쥐의 수명(일 수)을 폐 종양 발병 여부($\Delta=1$ : 발병, $\Delta=0$ : 발병하지 않음)에 따라 분류한 데이터다. 당시 연구자들은 폐 종양이 쥐에게 치명적이라는 가정 하에, 두 그룹에서 쥐에게 폐 종양이 발병하는 나이를 모델링하였다. 이를 위해 Kaplan-Meier estimator를 사용하였으며, 그 결과 아래 실선(일반환경)과 점선(무균환경)과 같이 나타났다.

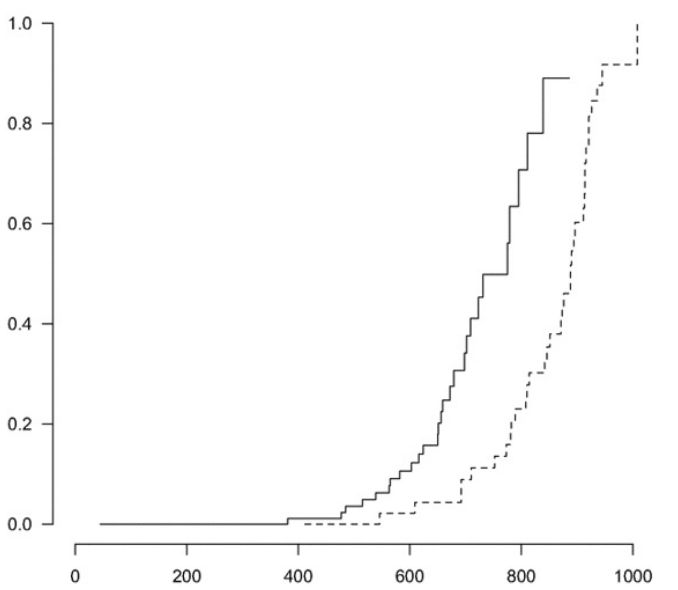
이로부터 무균 환경에서 쥐의 폐 종양 발병 나이는 일반 환경보다 확연히 늦다는 결론을 얻을 수 있었지만, 사실 이는 잘못된 과정이었다. 폐 종양이 쥐에게 치명적이라는 가정이 잘못되었고(사실은 치명적이지 않다고 한다), 폐 종양이 발견된 쥐($\Delta=1$)의 수명이 곧 폐 종양의 발병 나이와 유사할 것이라는 가정이 잘못된 것이다.

이를 옳게 추정하는 과정은 다음과 같다. 각각의 쥐($i$)를 관측한 순간(=쥐가 사망한 순간)($T_i$), 쥐는 폐 종양에 걸려있거나($\Delta_i=1$) 걸려있지 않다($\Delta_i=0$). 즉, 폐 종양에 걸린 나이($X_i$)는

를 만족한다. 쥐가 사망한 순간에만 폐 종양 여부가 관측되었기 때문에, 쥐의 폐 종양 발병 나이의 누적분포함수 $F$를 추정하기 위해

와 같이 log likelihood function을 정의한다. $l(F)$를 최대화하는 $\hat{F}$를 추정하기 위해

의 (greatest) convex minorant의 left derivative를 활용할 수 있다.(이론적 근거는 2주차에 계속) 이번 예시도 앞선 것과 유사한 맥락을 갖는다.

 

1.3 The Transmission Potential of a Disease

마지막으로 살펴볼 예시는 불가리아의 A형 간염에 감염된 인구 수이다. A형 간염과 같은 전염성이 있는 바이러스는 '얼마나 잘 전염되는가'가 주목해야 할 특징이다. 이를 Transmission Potential이라 하며, 이 값이 1보다 클 경우 감염병 유행의 위험이 있다.

짧은 감염 주기를 갖는 전염병의 Transmission Potential $R_v$는

를 따르며 $\lambda$는 감염 강도, $V(x)$는 나이가 $x$살인 사람에게 항체가 없을 확률, $\mu$는 사망률이다. 추정하고자 하는 것은 감염 강도 $\lambda$이며, 1.2에서의 절차와 유사하게 어느 한 시점에 표본 집단에 대해 항체 보유 여부를 조사함으로써 항체를 보유하면 이미 감염되었고, 항체를 보유하지 않으면 잠재적으로 감염되거나 아예 감염되지 않을 사람으로 판단할 수 있다.

---

 

2. Censored Data

Censored Data (중도절단 데이터)란 정확한 사건 발생 시점을 알 수 없는 데이터이다. 일반적으로 사건 발생 시점을 아는 데이터인 Complete Data와는 반대로, '실패' 또는 '죽음'을 관찰하는 경우(Ex. 수명, 어떤 약의 지속시간 등) 관측하는 시점마다 각 객체는 '아직 실패하지 않음'과 '실패'의 상태 중 한 가지로 나타난다. 아직 실패하지 않은 경우 실패(=사건의 발생)의 순간이 해당 시점 이후의 어딘가에 존재할 것이라고 짐작할 수 있다. 이러한 경우는 Censored Data와 Complete Data가 혼재된 형태로 나타난다.

Right Censored Data는 직전에 설명한 바와 같은 Censored Data의 한 유형이다. 시간이 흐름(오른쪽 방향)에 따라 각 객체에서 사건이 발생함으로써 더 이상 '생존하지 않은' 상태가 된다. 관측 시점에서는 중도 절단된 '실패' 데이터와 '아직 생존한' 데이터를 볼 수 있다. '아직 생존한' 데이터의 경우 실패 시점을 정확히 알 수 없으며, 어떤 구간 안에 실패 시점이 존재할 것이라고 추측할 수 있다.

Left Censored Data는 테스트 시작 전에 이미 '실패'한 데이터이다. Interval Censored Data 중 구간의 낮은 쪽이 0인 데이터이며, 현실에서 거의 찾아보기 힘든 유형이다.

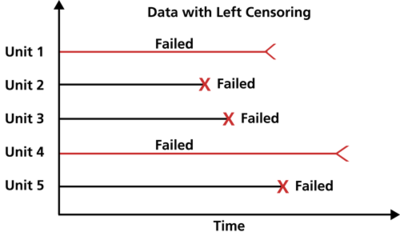
Interval Censored Data는 사건 발생 시점의 하한과 상한까지 알려진 Censored Data의 한 유형이다. 실험 객체에 대해 여러 번 관측을 할 때, $i$ 시점에서는 실패하지 않았지만 $i+1$ 시점에서는 실패한 경우 사건 발생 시점(=데이터)을 하나의 구간으로 나타낼 수 있다.

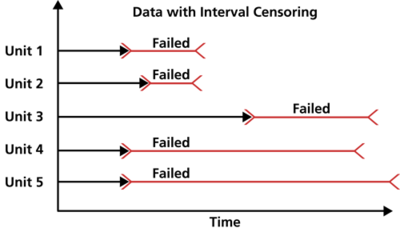
Type I Censored Data는 미리 정해둔 시간이 다 되어 테스트가 중단되는 경우이다. 이때 종료 시점까지 실패가 발생하지 않은 데이터는 종료시점에 Right-censoring 되어, 실패 시점이 구간으로 나타나게 된다.

Type II Censored Data는 미리 정해둔 실패 횟수가 다 되어 테스트가 중단되는 경우이다. 이때 종료 시점까지 실패 횟수에 도달하지 않은 데이터는 종료시점에 Right-censoring 된다.

지금부터 여러 유형의 Censoring 모델을 살펴보자.

2.1 Binary Censoring

어떤 상품이나 서비스에 대한 지불할 의향이 있는 금액(Willing To Pay, 이하 WTP)을 모델링하자. 같은 상품이라도 지불 주체($i$)마다 생각하는 '구매하기에 합리적인 가격의 최댓값'($y_i$)가 존재하며, 상품 가격($r_i$)보다 높을 경우 해당 제품을 구매할 것($w_i=1$)이다. 즉,

$w_i$ : 구매 의향 (구매한다($w_i=1$), 구매하지 않는다($w_i=0$)
$r_i$ : 판매자가 제시하는 상품 판매 가격
$y_i$ : 구매자가 생각하는, 상품을 구매하기에 합리적인 가격

이며, $P(y_i =r_i)=0$이라 가정하자. 판매자의 입장에서 가장 알고 싶은 정보는 $y_i$이며, $y_i$의 추정값을 $r_i$로 설정할 것이다. 고객의 정보($x_i$)를 바탕으로 $y_i$를 추정하는 가장 간단한 모델 형태는

을 만족하는 Linear Model이다. noise인 $u_i$가

을 만족한다고 가정하면, 제시된 가격에 고객이 상품을 구입할 확률을 다음과 같이 모델링할 수 있다.

하지만 $u_i$의 이분산성과 비정규성을 무시하는 가정은 Binary Censoring 과정에서 우려되는 것이 타당하다고 한다.(함부로 가정하기 어렵다는 의미인 듯 하다) 또한 $y_i \ge0$이 가정된 상황에서 Linear Model을 적용하는 것은 이상적이지 못하여

와 같이 Type I Tobit Model을 적용하거나

와 같이 $y_i \ge 0$을 유지하면서도 WTP가 0인 고객을 충분히 모델링할 수 있는 형식이 필요하다. 이를 바탕으로 구성한 '제시된 가격에서 고객이 상품을 구매할 확률'은

로 나타난다.

 

2.2 Interval Coding

2.1에서와 유사하게, 알려지지 않은 $y_i$를 추정하고자 한다. 달라진 점은 $y_i$의 정확한 값을 추정하는 것이 아닌, 미리 설정한 특정 구간 안에 속하도록 모델링하는 것이다. 즉,

으로 정의하고, 각각의 $j=0,~1,~\cdots,~J$마다, $y_i$가 $j$ 구간에 속할 확률인 $\mathrm{P}(w_i=j~|~\mathbf{x}_i)$를 아용하여 $y_i$를 모델링하는 것이다. 이러한 데이터를 Interval Censored Data라 한다.

위와 같은 interval censored data인 $y_i$를 $y_i=\mathbf{x}_i\beta+u_i$를 만족하는 선형모델로 모델링해보자. 즉 $y_i$를 결정하는 요소인 $\beta$,$\sigma$를 추정하는 것이다. ($u_i~|~\mathbf{x}_i,~r_i~\sim~N(0, \sigma^2)$임을 기억하자) $\beta$,$\sigma$에 대한 maximum likelihood function은 다음과 같이 구성된다.

 

2.3 Censoring from Above and Below

관측할 데이터에 상한 또는 하한을 설정하여 Right Censored Data 또는 Left Censored Data로서 관측할 수 있다. 예를 들어 사람들의 재산을 조사한다고 할 때, 너무 큰 금액대를 조사하는 것은 큰 의미가 없어보인다. Right Censored Data의 분포 함수를 추정하는 방법을 구체적으로 알아보자.

상한값($r_i$)에 대하여, 본래 관측치($y_i$)는

인 $w_i$로 대체된다. $w_i$는 상한값($r_i$)을 초과한 값을 갖지 않는 Right Censored Data이며, $w_i$의 cdf($F$)와 pdf($f$)를 추정하고자 한다. 자명하게도 $w_i \le r_i$이며, $w_i$의 Support를 $w<r_i$와 $w=r_i$인 경우로 나누어 생각할 수 있다.

• $w<r_i$인 경우
  관측치($y_i$)가 상한($r_i$)에 닿지 못했음을 의미하므로
  $\mathrm{P}(w_i \le w~|~\mathbf{x}_i,~r_i) = \mathrm{P}(y_i \le w~|~\mathbf{x}_i) = F(w~|~\mathbf{x}_i~;~\theta)$ 로 나타난다.

• $w=r_i$인 경우
  관측치($y_i$)가 상한($r_i$) 이상임을 의미하므로
  $\mathrm{P}(w_i=r_i~|~\mathbf{x}_i,~r_i) = \mathrm{P}(y_i \ge r_i~|~\mathbf{x}_i) = 1-F(r_i~|~\mathbf{x}_i~;~\theta)$ 로 나타난다.

위의 과정에서 $y_i$와 $r_i$의 독립성이 가정된다. 의미상으로 보아도 두 변수는 독립임이 자명하다. (상한값이 관측치에 영향을 받진 않으므로) 이를 바탕으로, $w_i$의 pdf($f$)를 추정하는 log likelihood function을 다음과 같이 구성할 수 있다.

이때 $y_i~|~\mathbf{x}_i~\sim N(\mathbf{x}_i\beta,~\sigma^2)$이 가정된다면 위의 과정을 거친 모델을 Censored Normal Regression Model이라 한다. 정규성이 가정된 상태에서 $w_i$의 pdf($f$)를 추정하는 log likelihood function은 다음과 같이 구성될 수 있다.

($\phi$는 표준정규분포의 pdf, $\Phi$는 표준정규분포의 cdf이다.)