[2주차] Nonparametric MLE for the type-I interval censored data

참고교재

• Groeneboom and Jongbloed (2014), Nonparametric Estimation under Shape Constraints, Cambridge University Press.

 

1. Monotone Regression

$x_i$가 고정값이며 증가함에 따라 $y_i$가 확률변수

의 실현값이라 하자. 여기서 $r$은 $x_i$를 통해 $Y_i$를 설명하고자 하는 함수이며, $\epsilon_i$는 $\mathrm{E}(\epsilon_i)=0$을 만족하는 확률변수(노이즈)이다. 우리의 목표는 단조함수 $r$을 추정하는 것이다. (단조 증가 or 단조 감소)

단조 증가가 가정된 함수 $r$을 추정한다고 하자. 관측에 의해 얻어진 실현값은 노이즈($\epsilon_i$) 때문에 단조성이 나타나지 않을 수 있다. ($y_i > y_{i+1}$인 실현값이 존재할 수 있다) 그럼에도 실현값만을 참고하면서, 실현값을 가장 잘 설명하는 단조 증가함수가 무엇일지 추정하는 과정이다.

 

다음 데이터를 예시로 살펴보자. 12세~18세 여자 아이들의 신장을 조사한 데이터다.

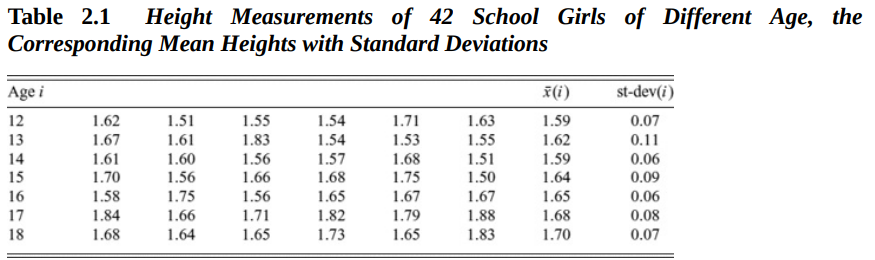
이때, 나이에 따른(12세~18세) 여자 아이들의 신장의 경향성을 설명하는 함수 $r$을 모델링하고자 한다. 그러한 $r$을 가장 잘 나타낸 $\hat{r}$은 다음과 같이 나타낼 수 있다.

즉, 단조 증가하는 함수 중 위의 quadratic form을 최소화하는 $r$이 우리가 원하는 함수라는 뜻이다. $\hat{r}$을 찾기에 앞서, 위 식은 오직 함수 $r$의 이산적인 함숫값에 의해서만 결정된다. 즉 $x_i$가 아닌 곳에서의 함숫값은 위 식의 최소화에 영향을 주지 않으므로, $x_i$가 아닌 점에서 $r$의 함숫값은 상수함수라 가정한다.

Lemma 2.1에서는 위와 같은 상황에서 $\hat{r}$의 필요충분조건을 서술한다. 어차피 $\hat{r}$의 $x_1,~x_2,~\cdots,~x_n$에서의 함숫값만 결정하면 되므로 $\hat{r}=(\hat{r}(x_1),~\hat{r}(x_2),~\cdots,~\hat{r}(x_n))$인 벡터를 추정하는 것으로 생각할 수 있다.

Lemma 2.1
$\hat{r}$이 convex cone $C=\{(r_1,~r_2,~\cdots,~r_n)\in\reals^n ~|~ r_1 \le r_2 \le ~\cdots r_n\}$에서 strictly convex function

을 최소화하는 것의 필요충분조건은

이다.

위 필요충분조건이 말하는 바는, 기본적으로 $i=1,~2,~\cdots,~n$일 때 부등식이 성립하면서도 추가로 $\hat{r}_{i+1}>\hat{r}_n$이거나 $i=n$일 때는 등식까지 성립한다는 것이다.

Lemma 2.1 Proof
1. 부등식($\Leftrightarrow$)
벡터 $v^{(i)}=(0,~\cdots~0,~,1~,~\cdots,~1)$ ($i^{th}$ 성분까지 $0$, 그 이후로는 $1$, $1 \le i \le n$)을 정의하자. 그렇다면 모든 $i$와 모든 $\epsilon>0$에 대하여 $\hat{r}-\epsilon v^{(i)} \in C$이다. $Q(r)$이 strictly convex 함수이므로

는 자연스럽다. ($Q(r)$을 최소화하는 $\hat{r}$에서 어떤 방향으로든($\epsilon v^{(i)}$) 벗어나면 $Q(r)$의 값은 커진다.)

이때, $Q(r)$의 정의에 의해

이므로

이다.

2. 등식($\Leftrightarrow$)
$\hat{r}_{i+1}>\hat{r}_i$ 조건 하에, 충분히 작은 $\epsilon>0$에 대하여 $\hat{r}_i+\epsilon<\hat{r}_{i+1}$이 성립하므로 $\hat{r}+\epsilon v^{(i)} \in C$이다. 따라서

이고,

이다. 1에서 증명한 사실에 의해

이다.

 

Lemma 2.1에 의해,

를 만족하는 $\hat{r}$을 정의할 수 있다면 이것이 곧 $Q(r)$의 최소화원이 된다. 이때 $\hat{r}$을

의 convex minorant의 left derivative로 정의한다면 위 조건을 만족하게 되어, $Q(r)$의 최소화원이 될 수 있다. 12세~18세 여자 아이들의 평균 신장의 편차($\bar{x}_i-\bar{x}$) 데이터를 기반으로 점들을 정의하고, 이것의 convex minorant을 그린 결과는 다음과 같다.

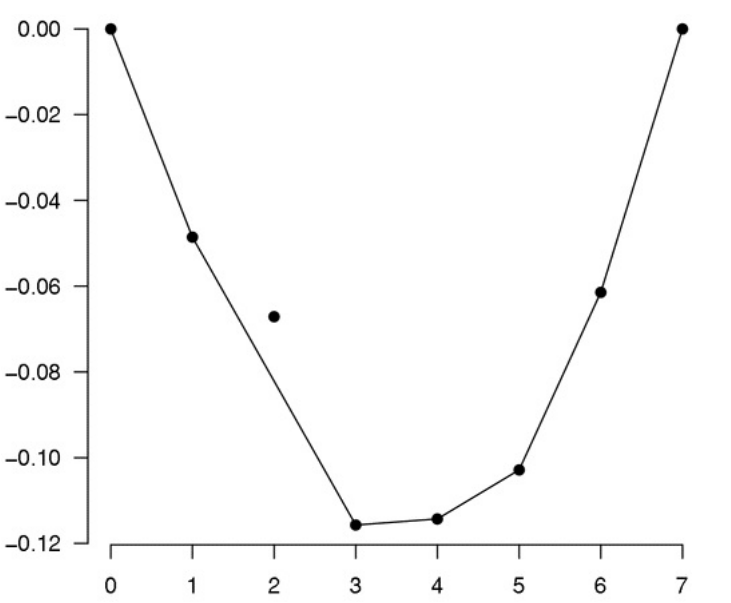
convex minorant는 convex한 꼴을 이루기 때문에, 실선의 기울기는 단조 증가한다. 따라서 단조 증가하는 $r$의 추정치로서 사용하기에 적합하며, Lemma 2.1은 이 기울기가 최소화원임을 보장한다.

일반적으로는 평균 신장의 편차가 아닌, 평균 신장 데이터를 기반으로 convex minorant를 그리지만, 명확한 시각화를 위해 편차를 활용하였다. 편차를 이용하더라도 원래 구하고자 하던 기울기는 어렵지 않게 구할 수 있다.

 

2. Estimation from Current Status Data

이번에 살펴볼 데이터는 1988년 오스트리아 남성 230명을 대상으로 조사한 Rubella(풍진) 발병 여부 데이터다.

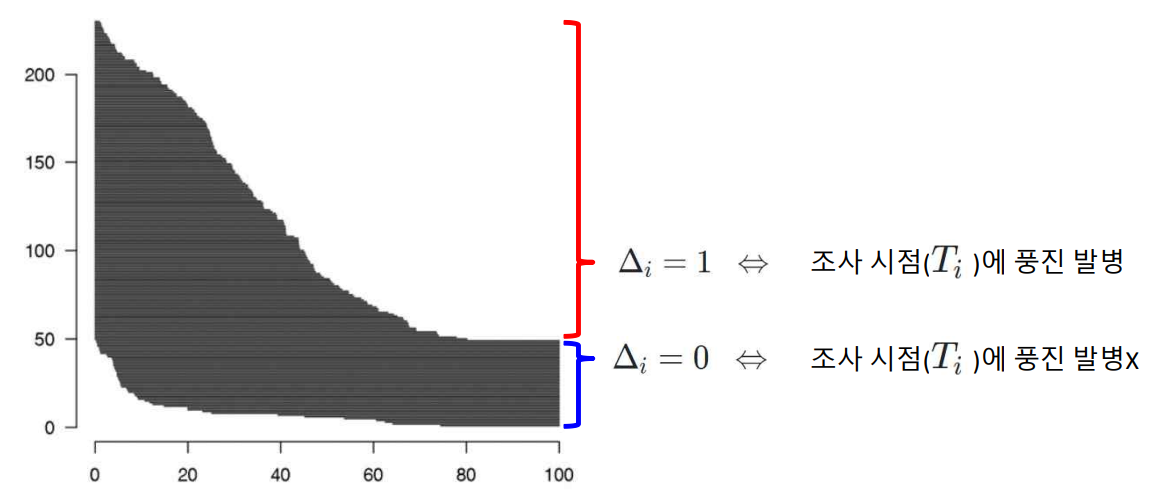
$T_i$ : [관측] 각 남성의 태어난 연도로부터의 조사 시점(years)
$\Delta_i$ : [관측] 풍진 발병 여부 (발병했다($\Delta_i=1$), 발병하지 않았다($\Delta_i=0$))
$X_i$ : [추정] 오스트리아 남성에게 풍진이 발병하는 나이(years)
$F$ : [추정] 나이에 따른 풍진 발병 분포 함수(CDF)

이로부터 오스트리아 남성의 풍진 발병 나이 함수($F$)를 추정하자. 질병의 특성을 고려하여, 풍진이 한 번 발병하면 평생 지속된다고 가정한다. 관측 데이터 $t_i$를 $t_1<t_2<\cdots<t_n$이 되도록 재배열한다.

각 데이터(남성)에 대하여, 조사 시점에 풍진이 발병되었을 확률은

이며, 조사 시점에 풍진이 발병되지 않았을 확률은

이다. 이로부터 $F$에 대한 log likelihood function을

로 정의할 수 있다. 이제 문제는 $l(F)$를 최대화하는 $\hat{F}$를 찾는 것이다.

앞선 예시에서와 같은 이유로 $\hat{F}$는 $t_i$ 이외의 점에서 상수함수로 가정할 수 있다. Lemma 2.3은 이러한 문제에서 최대화원 $\hat{F}$이 무엇인지 알려준다.

Lemma 2.3
다음과 같이 $P_i$를 정의하자.

$\hat{F}(t_i)$를 $P_i$로 만든 convex minorant의, $P_i$에서의 left derivative로 정의하면 $\hat{F}$는 $l(F)$의 유일한 최대화원이다.

Lemma 2.3 Proof
1. 최대화원
$l(F)$를 잘 정의하기 위해 다음 두 가지를 가정하자.

• $\delta_1=1$
• $\delta_n=0$
  $P_i$의 정의에 의해, $P_i$로 만든 convex minorant의 기울기는 $0$ 이상 $1$ 이하임을 알 수 있다. $\delta_1=1$을 가정하여 $\log F(t_1)$을, $\delta_n=0$을 가정하여 $\log F(t_n)$을 잘 정의하도록 한다.

$l(F)$는 strictly concave 함수이므로, $F(t_1) \le F(t_2) \le \cdots \le F(t_n)$을 만족하는 모든 $F$에 대하여

임을 보이면 $\hat{F}$이 $l(F)$의 최대화원임이 증명된다. 위 부등식의 의미는, $\hat{F}$로부터 어떤 방향으로라도 멀어진다면 $l(F)$의 기울기가 감소(or 0)한다는 뜻이다.

이므로, $I_1-I_2 \le 0$임을 보이자. $P_i$로 만든 convex minorant에서 꺾이는 점(=convex minorant가 지나는점)을

이라 정의하자. $t_i$ 이외에서 $\hat{F}$는 상수함수라고 정의하였으므로

가 성립한다.

1-1. $I_1 \le 0$

이고, $F(t_1) \le F(t_2) \le \cdots \le F(t_n)$의 특성에 의해 어떤 $\alpha_m \ge 0$에 대하여

로 나타낼 수 있다. 따라서

이고, $I_1 \le0$이다.

1-2. $I_2 = 0$

이다. $i_{j-1}<i\le i_j$에서 $\sum_{i=1}^n \delta_i$는 직각삼각형의 높이이고, $\hat{F}(t_i)$는 기울기가 되어 $\sum_{i=1}^n\hat{F}(t_i)$는 (기울기 $\times$ 밑변 $=$ 높이)가 되어 $\sum_{i=1}^n \delta_i$와 같아진다.

위의 두 사실로부터

이 성립한다.

2. 유일성
최대화원 $\hat{F}$가 유일하기 위해선

가 성립해야 한다. 즉, 등호가 성립할 수 없음을 보일 것이다.

이고, 이는 convex minorant가 모든 $P_i$를 지나는 것과 동치이고, 모든 $i$에서 $\delta_i=1$임과 동치다. 이는 앞서 세운 가정인 $\delta_n=0$에 모순이므로,

은 불가능하다. 따라서 최대호원 $\hat{F}$는 유일하다.

 

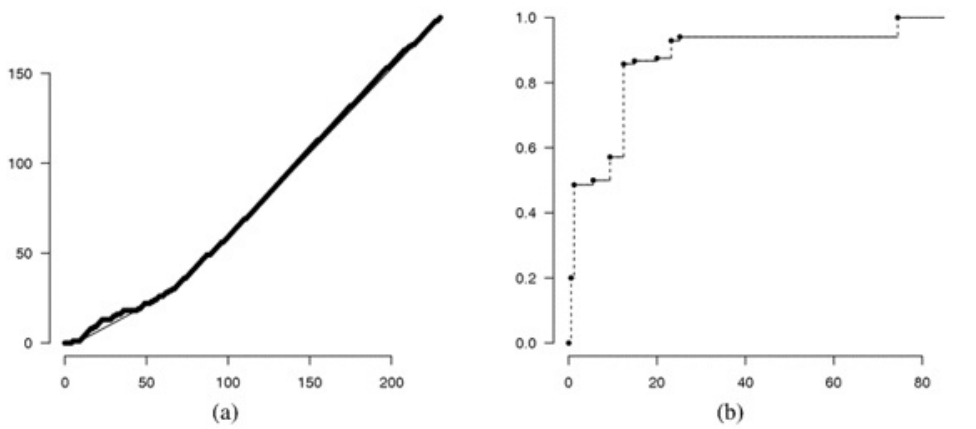
풍진 발병 데이터의 $P_i$와 이들로 만든 convex minorant는 (a)와 같고, 이로부터 추정한 풍진 발병 나이 분포함수(CDF) $\hat{F}$는 (b)와 같다. 대부분 20대 이후에는 풍진 바이러스를 보유함을 알 수 있다.