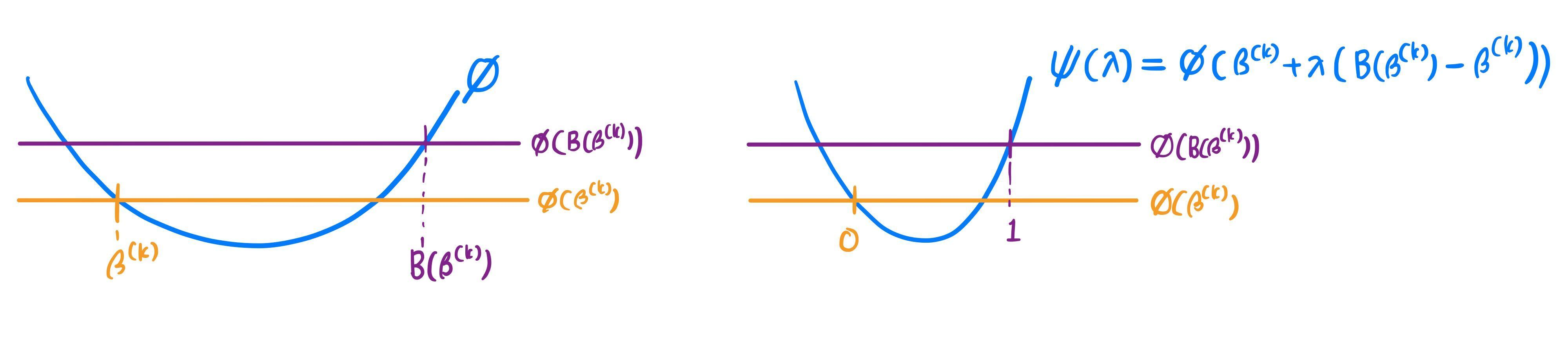참고교재
- Groeneboom and Jongbloed (2014), Nonparametric Estimation under Shape Constraints, Cambridge University Press.
1. Review
지난 2.1절에서는 단조 증가하는 함수 r을 추정하는 방법을 알아보았다.
Lemma 2.1
r^이 convex cone C={(r1, r2, ⋯, rn)∈Rn ∣ r1≤r2≤ ⋯rn}에서 strictly convex function
Q(r)=21i=1∑n(ri−yi)2wi
을 최소화하는 것의 필요충분조건은
j=1∑ir^jwj{≤∑j=1iyjwj=∑j=1iyjwjfor i=1, 2, ⋯, nif r^i+1>r^i or i=n
이다.
r의 추정함수 r^을
(0,0), (w1, w1y1), ⋯, (j=1∑nwj, j=1∑nwjyj)
의 convex minorant의 left derivative로 정의한다면 Lemma 2.1의 등식/부등식 조건을 만족하여, Q(r)의 최소화원으로서 역할을 할 수 있었다. 여기서 기억해야 할 점은, 우리가 Q(r)과 같은 quadratic form의 최소화원을 알고 있다는 것이다.
2. Newton Algorithm
Newton Algorithm은 (convex) function의 최소화원을 찾기 위한 알고리즘이다. 즉, 어떤 (convex) function ϕ:Rn→R를 최소화하는 θ^∈Rn를 찾는 알고리즘이다. 알고리즘은 θ(0), θ(1),θ(2),⋯와 같이 점진적으로 θ^를 찾아가게 된다.
- 초기값 θ(0)를 설정
- k≥0에 대하여, θ(k+1)=A(θ(k))
=θargmin(ϕ(θ(k))+(θ−θ(k))T∇ϕ(θ(k))+21(θ−θ(k))T∇2ϕ(θ(k))(θ−θ(k))) 으로 정의
- 종료조건 달성 시까지 2를 반복
하지만 Newton Algorithm은 ϕ의 실제 최소화원으로 수렴을 보장하지 못한다는 단점이 있다. 이는 ϕ가 convex function이더라도 보장되지 않는다.
3. Iterative Convex Minorant Algorithm
Newton Algorithm을 보완할 새로운 알고리즘을 알아보자. 이 알고리즘은 convex function이 유일한 최소화원을 갖는다면, 반드시 그 최소화원으로의 수렴성을 보장하는 알고리즘이다. 다음과 같이 용어를 정의하고, 3가지를 가정하자.
ϕ : 목적함수(objective funtion) - 최소화되길 원하는 함수
C={r∈Rn : r1≤r2≤⋯≤rn} : convex set
- ϕ : convex, continuous on C
- ϕ : continuously differentiable on {β∈Rn : ϕ(β)<∞}
- β^ : unique minimum of ϕ on C exist
이로부터 다음 동치관계가 성립한다.
β^=β∈Cargmin ϕ(β) ⇔ {<β^, ∇ϕ(β^)>=0<β, ∇ϕ(β^)>≥0 for all β∈C
이는 왼쪽과 같이 convex set 내부에 global minimum이 존재한다면 ∇ϕ(β^)=0이 되어 등식/부등식이 성립하고, 오른쪽과 같이 convex set 외부에 있더라도 최소화원은 convex set의 경계에 위치하게 되어 등식/부등식이 성립한다.
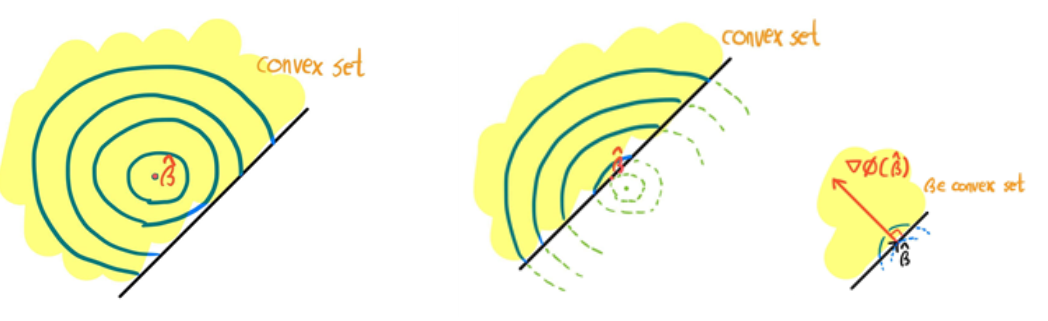
위 동치조건은 추후 Modified Iterative Convex Minorant Algorithm의 종료 조건으로 사용된다.
Iterative Convex Minorant Algorithm (이하 ICM)은 Newton Method와 유사한 방식으로 최소화원을 찾아간다.
- 초기값 β(0)을 설정
- 이전 값(β(k))에서의 함수 ϕ의 근사 함수의 최소화원을 다음 값(β(k+1))으로 설정
- 종료조건 달성 시까지 2를 반복
2번에서의 근사함수는 다음과 같이 정의된다. γ∈C 근방의 임의의 β에 대하여, ϕ(γ+(β−γ))의 근사함수는
ϕ(γ+(β−γ))≈ϕ(γ)+(β−γ)T∇ϕ(γ)+21(β−γ)TD(β−γ)=ϕ(γ)+21(β−γ+D−1∇ϕ(γ))TD(β−γ+D−1∇ϕ(γ))−21∇ϕ(γ)T(β−γ+D−1∇ϕ(γ))+21∇ϕ(γ)T(β−γ)=ϕ(γ)+21(β−γ+D−1∇ϕ(γ))TD(β−γ+D−1∇ϕ(γ))+cγ
where cγ=−21∇ϕ(γ)T(β−γ+D−1∇ϕ(γ))+21∇ϕ(γ)T(β−γ)=−21∇ϕ(γ)TD−1∇ϕ(γ),
D:positive diagonal matrix
이고, 이러한 근사 함수를 최소화하는 최소화원 B(γ)는
B(γ)=β∈Cargmin(ϕ(γ)+21(β−γ+D−1∇ϕ(γ))TD(β−γ+D−1∇ϕ(γ))+cγ)=β∈Cargmin(21(β−γ+D−1∇ϕ(γ))TD(β−γ+D−1∇ϕ(γ)))=β∈Cargmin(21i=1∑n(βi−γi+di1∂βi∂ϕ(γ))2di)
where di=Di,i
이다. B(γ)는 quadratic form이므로, 앞선 Lemma 2.1에서와 같이 convex minorant를 이용하면 B(γ)를 구할 수 있다.
이러한 알고리즘은 ϕ를 최소화하는 것이 아닌, ϕ의 근사함수를 최소화하는 과정을 나타낸다. 그렇다면 근사함수를 최소화하는 것이 ϕ를 최소화하는 것에 도움이 될까? Lemma 7.1은 그에 대한 일부 답변을 제시한다.
Lemma 7.1
앞선 가정을 만족하는 ϕ와, ϕ(β)<∞을 만족하는 모든 β∈C∖{β^}에 대하여, 충분히 작은 λ>0가 존재하여
ϕ(β+λ(B(β)−β))<ϕ(β)
가 성립한다.
즉, ICM의 방법이 ϕ를 최소화하는 방향임은 보장한다.
Lemma 7.1 Proof
ψ : [0,1]→R를 다음과 같이 정의하자.
ψ(λ)=ϕ(β+λ(B(β)−β))
[Claim] : ψ′(0+)=(B(β)−β)T∇ϕ(β)<0
만약 위 Claim이 증명된다면
ψ′(0+)≈λψ(0+λ)−ψ(0)<0,
ψ(0+λ)−ψ(0)=ϕ(β+λ(B(β)−β))−ϕ(β)<0
와 같이 Lemma 7.1이 증명된다.
다음 두 사실로부터,
B(β)T(D(β)(B(β)−β)+∇ϕ(β))=0
βT(D(β)(B(β)−β)+∇ϕ(β))≥0
다음 부등식이 성립한다.
(B(β)−β)TD(β)(B(β)−β)+ψ′(0)≤0
하지만 β∈C∖{β^}이므로 D(β)는 positive definite이고, 따라서
(B(β)−β)TD(β)(B(β)−β)>0 ⇒ ψ′(0)<0
가 성립한다.
Lemma 7.1은 감소 방향에 대한 해답은 주지만, β^까지 감소하는지에 (=최소화원으로의 수렴성) 대해서는 보장하지 않는다. 이를 보완하는 알고리즘을 소개한다.
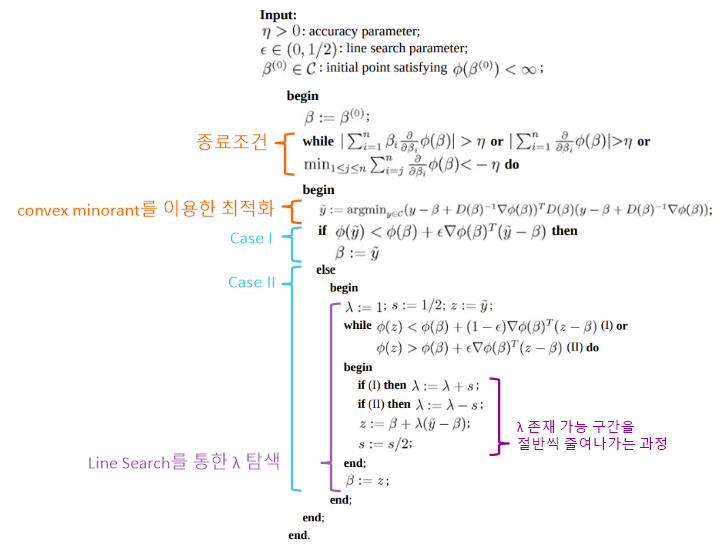
4. Modified Iterative Convex Minorant Algorithm
Modified Iterative Convex Minorant Algorithm (이하 MICM)은 ICM의 알고리즘에 β^으로의 수렴성을 더한 방법이다. ICM에서의 방법과 같이 β(0),β(1),β(2),⋯으로 β^를 점진적으로 찾아가며, 그 관계는 다음과 같다.
β(k+1)=C(β(k))={B(β(k)) if ϕ(B(β(k)))<ϕ(β(k))+(1−ϵ)∇ϕ(β(k))T(B(β(k))−β(k))x∈{y∈seg(β(k), B(β(k))) ∣ (1−ϵ)∇ϕ(β(k))T(y−β(k))≤ϕ(y)−ϕ(β(k))≤ϵ∇ϕ(β(k))T(y−β(k))} else
where ϵ∈(0, 0.5)
위 관계식을 그림으로 살펴보자. ϕ를 최소화하는 것이 목표지만, 이를 ψ 관점에서 살펴볼 것이다.
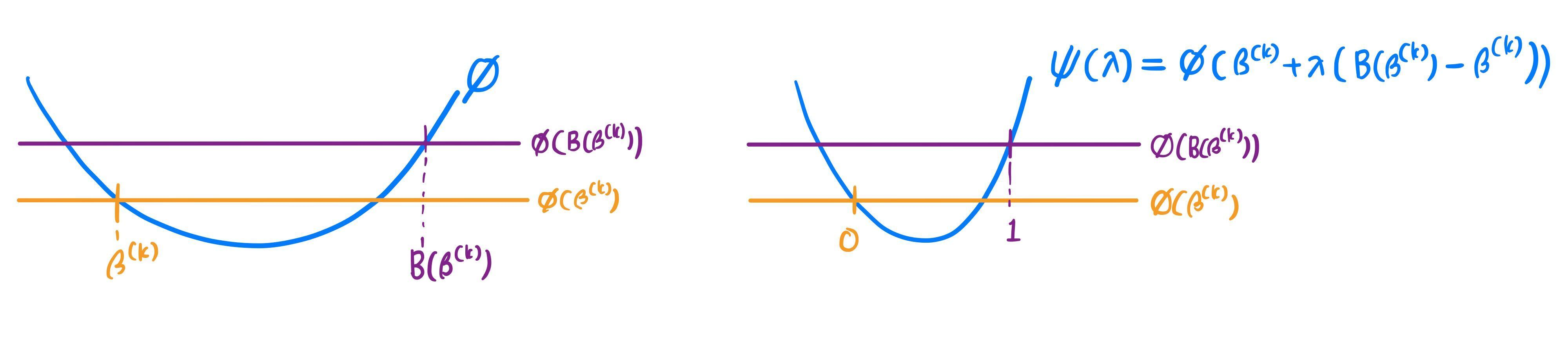
1) ϕ(B(β(k)))<ϕ(β(k))+(1−ϵ)∇ϕ(β(k))T(B(β(k))−β(k))
부등식의 오른쪽 항은 ϕ(β(k))+(1−ϵ)ψ′(0)과 같다. 이는 아래와 같이 기울기가 (1−ϵ)ψ′(0)이고 (0,ϕ(β(k)))를 지나는 직선이 λ=1에서의 함숫값과 같다.
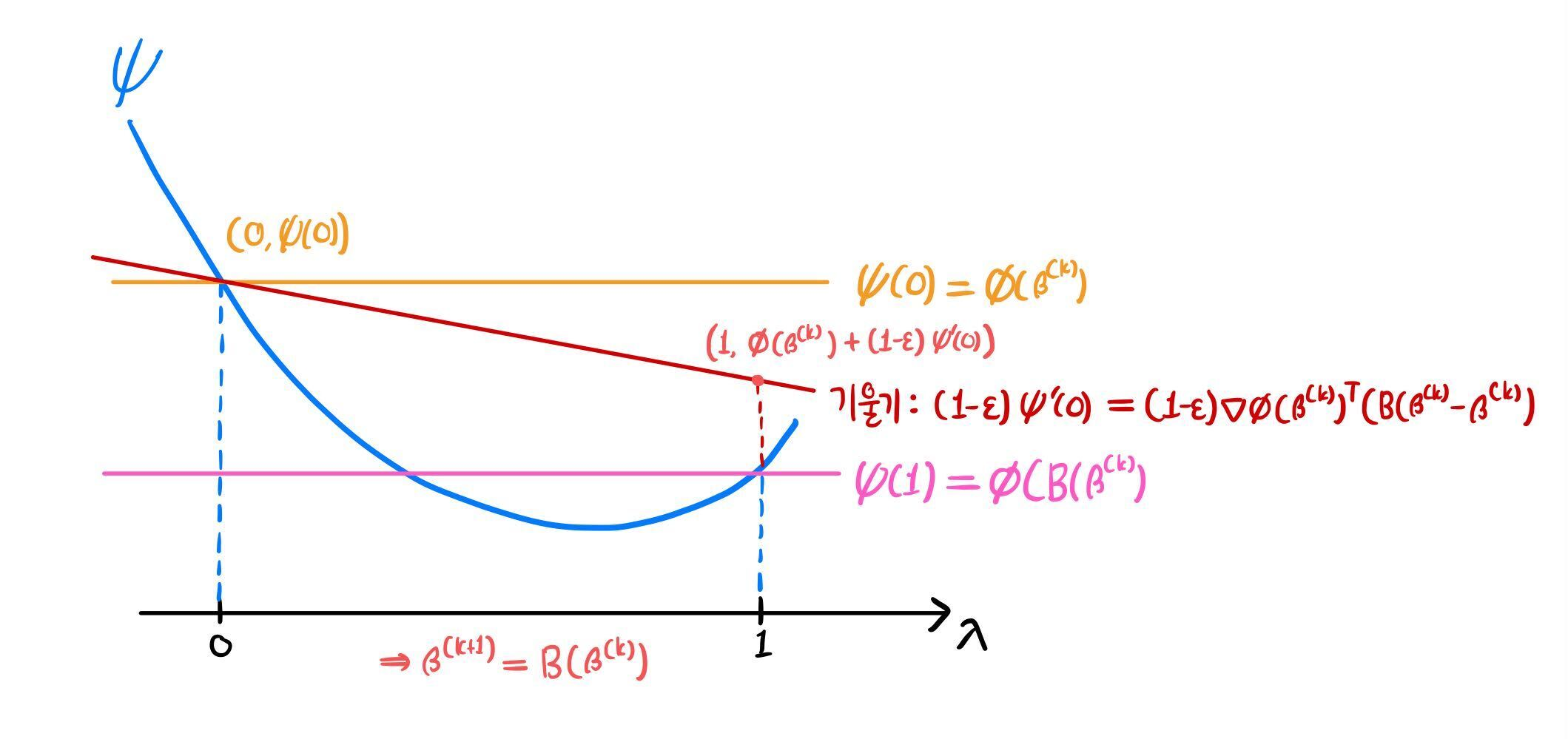
이 직선은 항상 감소하며, 기울기에 1−ϵ을 곱함으로써 그래도 이 직선보다는 더 감소했으면 좋겠다의 정도로 해석할 수 있다. 부등식 조건에서는 ϕ(B(β(k)))가 직선보다 아래에 위치하므로 충분히 감소했다고 판단하여 β(k+1)=ϕ(B(β(k)))로 정의하였다고 볼 수 있다.
2) ϕ(B(β(k)))≥ϕ(β(k))+(1−ϵ)∇ϕ(β(k))T(B(β(k))−β(k))
1)의 해석에 따라, 기대한 만큼 충분히 감소하지 못했을 경우다. 아래 그림은 그럼에도 ϕ(B(β(k)))<ϕ(β(k))인 상황이지만, 일반적으로 이렇다고 보장할 수 없다. 따라서 어떤 적절한 0<λ<1을 선택하여, 그 때의 ψ(λ)를 β(k+1)로 선정할 것이다.
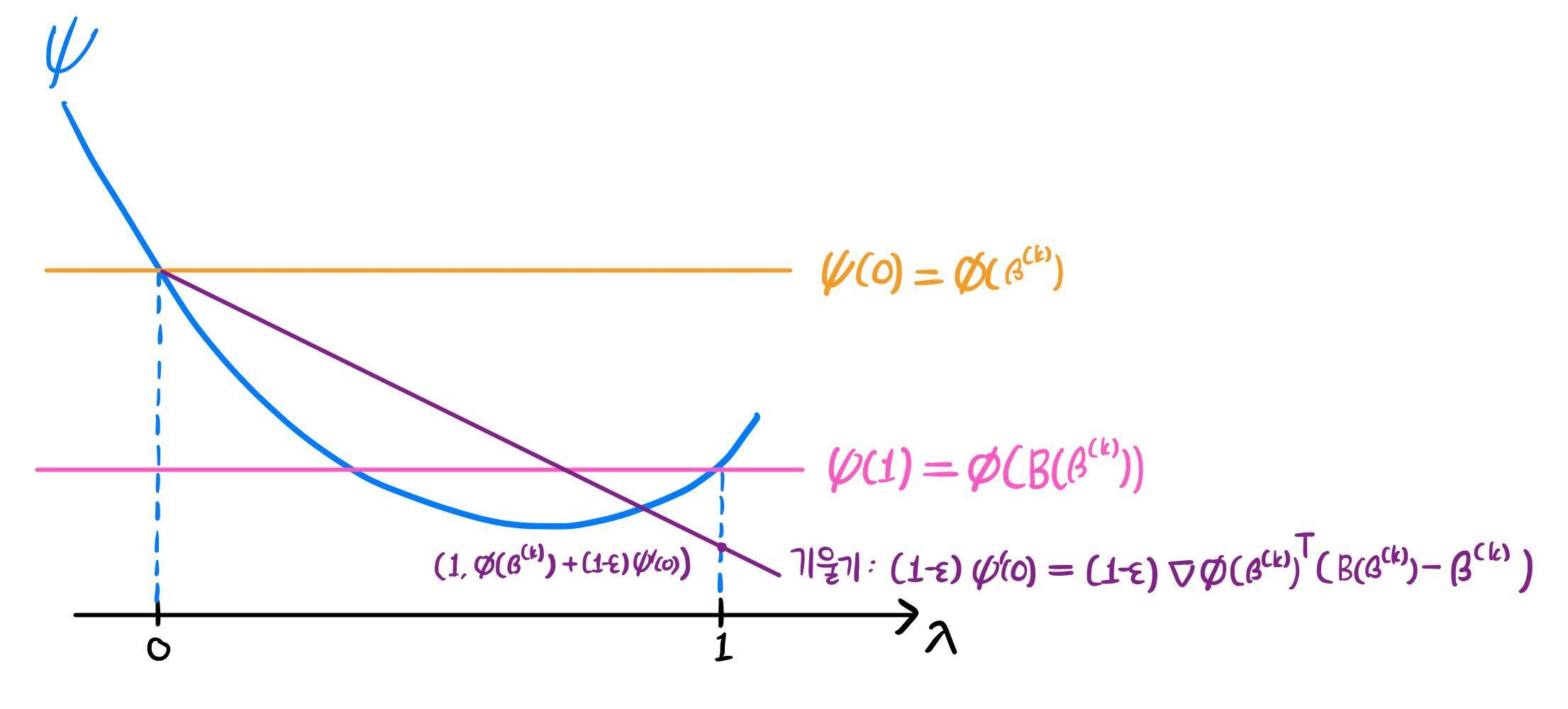
기대한 만큼 충분히 감소한 결과를 원하므로, 기울기가 (1−ϵ)ψ′(0)이고 (0,ϕ(β(k)))을 지나는 직선보다 아래 영역에서 λ를 선택할 것이다. 대신 너무 조금 감소하는 경우를 배제하기 위해 기울기가 ϵψ′(0)이고 (0,ϕ(β(k)))을 지나는 직선보다 위 영역으로 λ 범위를 제한한다. 아래 그림에서의 연두색 영역과 같다.
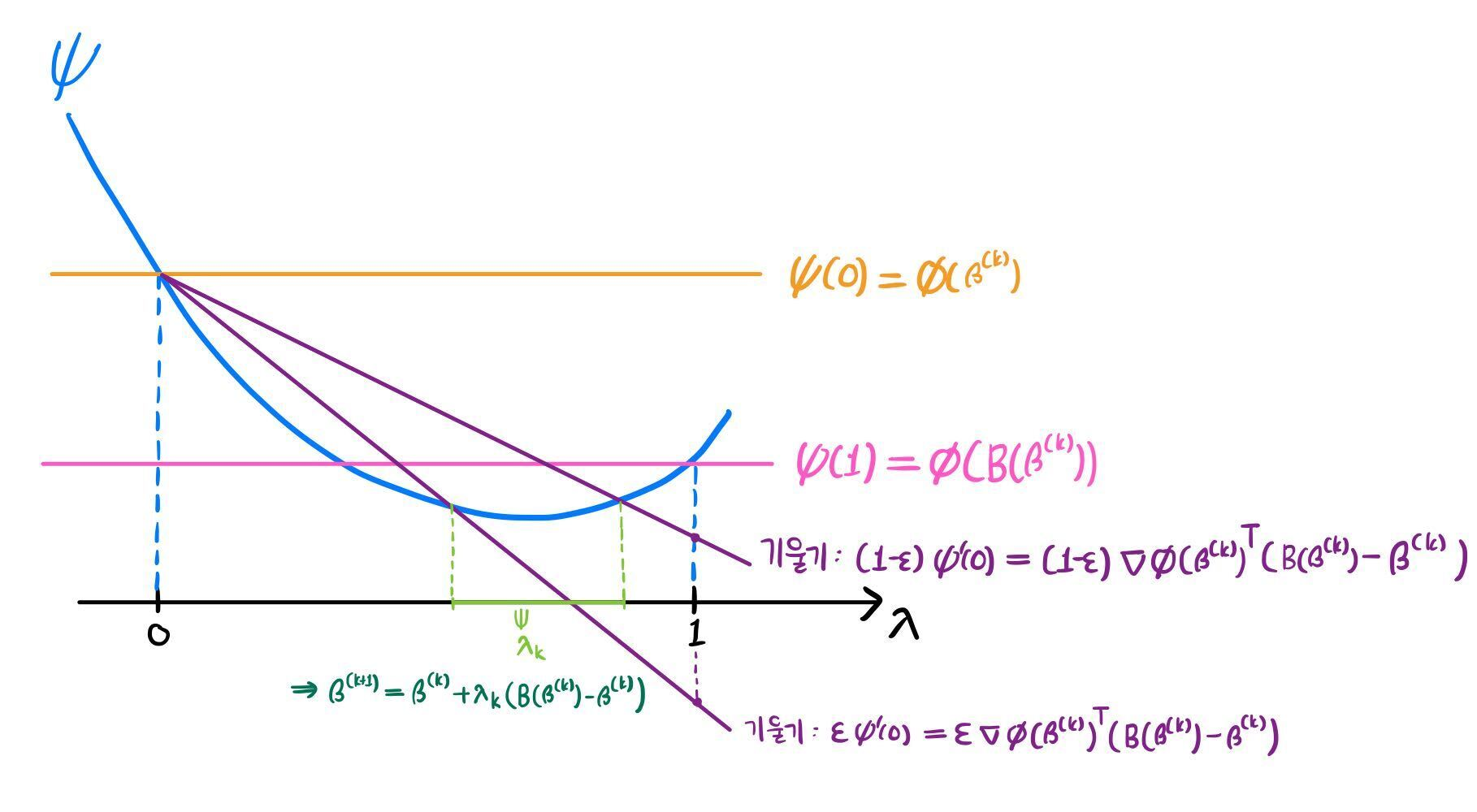
해당 영역 내의 아무 λk를 선택하여 β(k+1)=ψ(λk)=β(k)+λk(B(β(k))−β(k))로 정의한다.
이러한 알고리즘의 종료 조건은 다음과 같다.
i=j∑n∂βi∂ϕ(β^){≥0 for 1≤j≤n=0 for j=1
이는 다음 동치관계를 기반으로 결정되었다.
<β, ∇ϕ(β^)>≥0 for all β∈C ⇔ i=j∑n∂βi∂ϕ(β^){≥0 for 1≤j≤n=0 for j=1
Theorem 7.3은 MICM에 의해 β^으로 수렴함을 보인다.
Theorem 7.3
앞선 조건을 만족하는 ϕ:Rn→(−∞,∞]와, ϕ(β(0))<∞을 만족하는 β(k)∈C에 대하여, mapping β↦D(β)이 집합 K={β∈C : ϕ(β)≤ϕ(β(0))}에서 연속이 되도록 하는 positive definite diagonal matrix D를 선택하면, Iterative Convex Minorant Algorithm은 β^로 수렴한다.
Theorem 7.3 Proof
모든 k≥0에 대하여 β(k)∈K고, K는 compact이다.
⇒ [Enough to Show] : 모든 β∈K∖{β^}에서 Modified ICM 함수 C가 닫혀있다.
만약 닫힘성(closedness)가 증명되면 7.1절의 Theorem 7.1에 의해 수렴성이 보장된다. (교재 참고)
임의의 β∈K∖{β^}와 β(k)→β인 β(k)∈K에 대하여, γ(k)를
γ(k)∈C(β(k)), γ(k)→γ for some γ∈K
로 정의하자.
⇒ [Enough to Show] : γ∈C(β)
다음 사실로부터,
∇ϕ(β(k))→∇ϕ(β), B(β(k))→B(β)
1) ϕ(B(β(k)))≤ϕ(β(k))+(1−ϵ)∇ϕ(β(k))T(B(β(k))−β(k))
γ(kj)=B(β(kj)) for each j≥0
C(β)={B(β)} as β(k)→β
가 성립하므로
γ(kj)→B(β) as j→∞
γ=B(β)∈C(β)
가 성립한다.
2) ϕ(B(β(k)))>ϕ(β(k))+(1−ϵ)∇ϕ(β(k))T(B(β(k))−β(k))
MICM에 의해
ϕ(γ(k))−ϕ(β(k))∈[(1−ϵ)∇ϕ(β(k))T(γ(k)−β(k)), ϵ∇ϕ(β(k))T(γ(k)−β(k))]
이고, 충분히 큰 k에 대하여
β(k)→β, γ(k)→γ, ∇ϕ(β(k))→∇ϕ(β)
가 성립하므로
ϕ(γ)−ϕ(β)∈[(1−ϵ)∇ϕ(β)T(γ−β), ϵ∇ϕ(β)T(γ−β)]
이고, 따라서
γ∈C(β)=seg(β, B(β))
가 성립한다.
MICM의 전체 과정은 다음과 같다.