이번 블로깅에선 자료구조 중에서도 정말 자주 나오는 복잡도 에 대해 알아보자.

시간 복잡도

우선, 시간 복잡도란 무엇일까?

시간 복잡도란, 문제를 해결하는 데 걸리는 시간과 입력의 함수 관계 를 나타낸다.

쉽게 말해 우리가 만든 코드가 일을 끝마치는데 얼마나 걸리는지에 대한 척도이다.
어떠한 알고리즘의 로직이 얼마나 오랜 시간 이 걸리는지에 대한 척도로 기억해주면 좋을 것 같다.

빅오 표기법

보통 위에서 설명한 시간 복잡도를 빅오 표기법으로 나타낸다.
그렇다면 빅오 표기법이 무엇일까?
아래와 같은 코드가 있다고 가정해보자.

for(var i =0;i<10;i++){
    for(var j = 0; j<n;j++){
        for(var k =0;k<n;k++){
            if(true) console.log("빅오 표기법");
        }
    }
}

for(var i = 0;i<n;i++){
    if(true) console.log("빅오 표기법");
}

만약 위에 코드는 n의 입력을 받는다고 가정해볼때, 빅오 표기법 얼마나 출력될까?
바로 10n^2 + n 만큼이 출력될 것이다. 이때 n이 무한대로 뻗어나간다고 생각해보자. 그렇다면 저값은 어디에서 가장 영향을 많이 받을까?
바로 n^2이다. 다른 값들은 n-> ∞ 간다고 생각했을때 거의 값에 영향을 주지 않는다. 무시할만큼 미미하다.

n-> ∞
10n^2 + n = n^2에 논리이다.

그래서 이를 O(n^2) 이라고 나타내고, 이러한 방법을 빅오 표기법 이라고 한다.

시간 복잡도의 존재 이유

그렇다면 이러한 시간 복잡도 를 왜 구하는걸까?
이는 당연하게도 효율적인 코드로 개선하는데 쓰이는 척도가 된다.
O(n^2)의 시간 복잡도를 가지는 알고리즘과 O(n)의 시간 복잡도를 가지는 알고리즘 중에 어떤 것을 써야할까?

당연하게도 시간 복잡도가 적은 O(n)의 알고리즘을 사용해야한다.

Worst Case를 고려하는 시간복잡도

우선 아래 표는 시간 복잡표에 대한 평균 시간 복잡도와 최악의 시간 복잡도이다.

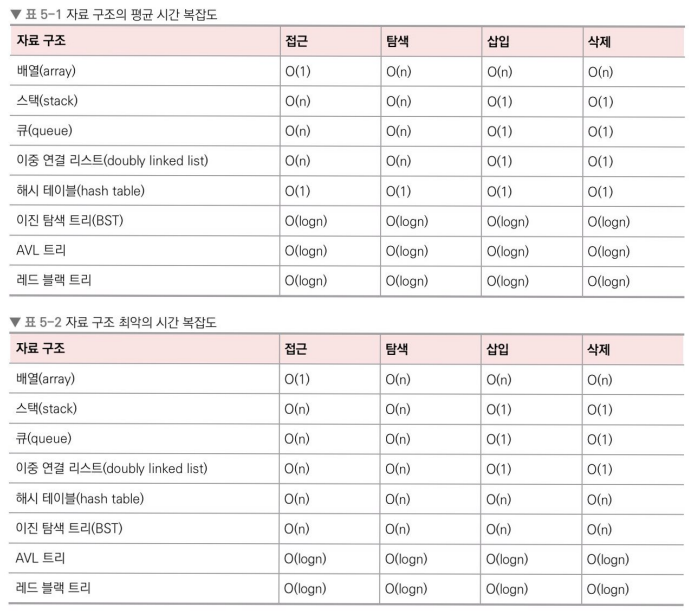
위에서 처럼 왜 n-> ∞ 보내면서 시간복잡도를 구할까?
우리가 개발자라면 best Case보단 worst Case 를 고려해야 한다.
당연하게도 대부분이 된다고 해도 worst Case에서 코드가 돌아가지 않는다면 이는 돌아가는 코드라고 할 수 없다.
이를 위해 n을 무한대로 보내 worst Case 를 만들어놓고 이를 시간복잡도로 규정하는 것이다. 최악의 경우를 대비하여 성공하면 당연하게도 다른 케이스들은 성공한다.

공간 복잡도

위에서 시간 복잡도에 대한 이해가 갔을 것이라고 생각한다.
우리가 알고리즘을 수행하기 위해 얼마나 걸리는지 시간에 대한 것이 시간 복잡도 구나!!

그렇다면 공간 복잡도 란 무엇일까?

공간 복잡도는 프로그램을 실행 시켰을 때 필요로 하는 자원 공간의 양을 말한다. 정적으로 변수 말고도, 동적으로 재귀적 함수를 인해 공간을 계속해서 필요로 하는 경우도 포함한다.

한마디로 코드를 돌릴때 필요로 하는 필요로 하는 공간의 양을 말하는 척도이다.

int a[1004];

예를 들어 이러한 코드가 있다면 가정해보면,
int형이 들어갈 공간 1004개가 필요로 되어진다.
바이트 기준으로는 1004 * 4 바이트의 크기를 가지게 된다. 이렇게 필요로 되어지는 메모리 양을 공간복잡도 라 한다.

마무리

이번 블로깅에선 복잡도 에 대해 알아보았다. 이 블로깅의 목적은 깊게 배우는 것이 아니라 개발자 대회에 낄 정도의 넒고 얕은 지식을 목표로 하고 있다. 이 블로깅을 통해서 전체적인 복잡도 에 대해 잡았으면 좋겠다. 그리고 감을 잡았고 좀 더 깊게 배우고 싶다면 이 블로깅의 키워드를 길로 잡아서 하나씩 공부해 나간다면 매우 도움이 될 것이라고 생각한다.

좀더 이야기를 붙이자면 시간 복잡도의 경우 빅오 표기법 말고도 더 다양한 방법이 있다. 이러한 부분도 공부하는 것이 깊이 있게 배우는데 도움을 줄 것이다.