들어가기 전

이번 블로깅에선 자료구조 중에서도 선형 자료 구조에 대해 집중적으로 넓고 얕게 배워보려 한다. 한번 차근차근 가보자.

선형 자료 구조란?

선형 자료 구조란, 요소가 일렬로 나열되어 있는 자료 구조를 말한다.

일자로 연결되어 있어서 선형 자료 구조 라는 말이 붙었다.
그렇다면 이에 대한 종류에는 어떤 것이 있는지 알아보자.

1. 연결 리스트

연결리스트는 데이터를 감싼 노드를 포인터로 연결해서 공간적인 효율성을 극대화 시킨 자료구조이다.
이게 무슨 말이냐면 데이터 형태가 데이터와 다른 데이터를 연결 짓는 부분으로 나뉘어져 있다. 이때 이 연결짓는 부분이 하나라면 싱글 연결 리스트 (Single Linked List)라고 하면 두개라면 이중 연결 리스트 (Double Linked List) 라고 한다.

조금 더 부연 설명을 하자면 데이터와 다른 데이터를 연결 짓는 포인터가 합쳐진 형태를 노드 라고 부르며 이 노드들이 연결 되어 있는 것을 연결 리스트 라고 부른다.
이때 가장 앞에 있는 노드를 head 라고도 부른다.
각각의 노드를 어떤 식으로 연결하나야 따라서 연결리스트의 종류가 변한다. 아래 그림을 참고하면 이해가 쉬울 것이다.

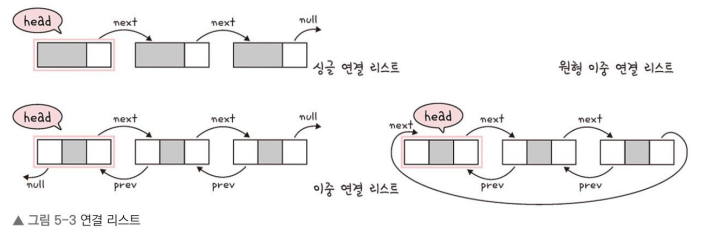
1. 싱글 연결 리스트 (Single Linked List)
   next 포인터만을 가지면서 현 노드에서 다음 노드만을 가리키는 형태이다.
2. 이중 연결 리스트 (Double Linked List)
   next 포인터와 prev포인터 두개를 가진 형태를 말하며 next 포인터는 다음 노드, prev 포인터는 이전 노드를 가리키는 형태이다.
3. 원형 이중 연결 리스트 (Circular Linked List)
   이는 이중 연결 리스트와 유사하지만 위에 그림처럼 마지막 노드가 헤드 부분을 가리키면서 순환이 가능하게 끔 만들었다. 이를 원형 이중 연결 리스트라고 부른다.

이 자료구조의 특징은 삽입과 삭제가 O(1) 이 걸리고, 탐색에는 O(n) 이 걸린다.
삽입과 삭제는 node를 그 부분을 끊고 새롭게 연결 시키면 끝이기 떄문에 상수 시간이 걸리며, 탐색의 경우는 데이터를 찾기 위한 기준이 없어서 head에서부터 그 노드를 탐색해야 되기 때문에 O(n)시간이 걸린다.

2. 배열

배열 (Array)는 같은 타입의 변수들 을 모아둔 집합의 형태이다.

크기가 정해져 있으며, 인접한 메모리 위체 있는 데이터를 모아놓은 집합이다. 또한 중복을 허용하고 순서가 있다.

탐색은 index기준으로 탐색하는 랜덤 접근이 가능하여 O(1) 시간이 걸린다. 배열의 가장 큰 특징은 이 index 부분에 있다. 이를 통해 빠르게 검색하고 데이터를 간닿게 쌓고 싶을 때 사용된다.

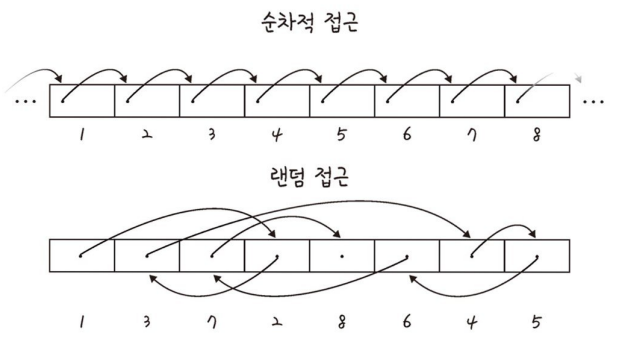
랜덤 접근 (Random Access)

랜덤 접근이라는 단어가 생소한 경우가 많을 것이다.
랜덤 접근은 임의의 인덱스에 해당하는 데이터에 접근할 수 있는 기능을 말한다. 이는 연결리스트처럼 검색 시 데이터를 순서대로 검색하는 순차적 접근 과 대조를 이룬다.

배열 VS 연결 리스트

그렇다면 위에서 설명한 두개의 차이가 뭘까? 비슷해 보이는데..
1. 접근 방법
첫번째로 바로 랜덤 접근과 순차적 접근이다.
배열은 몇 번째인지만 알면 바로 접근이 가능한 랜덤 접근 방법을 채택한다.
그에 비해 연결리스트는 요소를 알기 위해서는 순차적으로 확인해봐야 하는 순차적 접근을 사용해야 한다.
2. 데이터 추가 및 삭제
위에처럼 들어보면 그러면 배열 쓰면 좋은 거 아니야? 싶겠지만 데이터를 추가하고 삭제하는 부분은 연결리스트에서 강점을 가진다.
배열의 경우, 값을 추가하려면 그 값을 넣기 전에 한칸씩 뒤로 미는 과정이 필요하다. 그에 비해 연결리스트는 노드를 끊고 거기에 이어주면 그만이다.

이처럼 각각의 장단점이 있다.

3. 벡터

벡터(Vector)는 동적으로 요소를 할당할 수 있는 동적 배열이다.
기존 배열의 경우에는 크기가 정해져 있어서 이를 넘기면 작동이 불가능하다. 하지만 벡터는 이를 초월한 동적 배열의 형태를 가지고 있다.
보통은 배열의 형태를 따라간다. 이도 배열처럼 랜덤 접근이 가능해서 탐색은 O(1)이 걸린다. 또 삽입과 삭제는 O(n)이 걸린다.

여기서 하나 알아두면 좋은 것이 맨뒤에 요소를 삽입할때 O(1)의 시간이 걸린다.
이 이유가 벡터 같은 경우에는 크기를 증가시키는 것의 시간 복잡도가 amortized 복잡도 를 따른다.

amortized 복잡도 란 해당 연산의 최악의 경우에 해당하는 연산 순서열(operation sequence)를 수행했을 때의 연산의 평균적인 시간복잡도를 말한다.

이것이 무슨 말일까? 아래 그림을 봐보자.

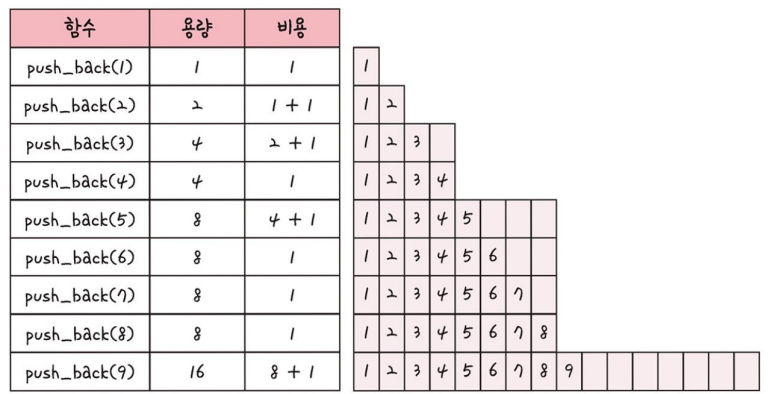
벡터는 크기가 유동적으로 바뀌는 구조인데, 이것이 값이 증가될때 계속 크기를 1씩 증가시키는 것이 아니다.
실제로는 위의 그림과 같이 2^n + 1 일 때, 크기를 증가시킨다.

뒤에 값을 붙이는 과정을 n번 했다고 가정하면 식은 아래와 같아진다.

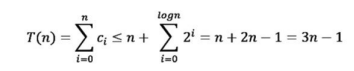
이를 n으로 나누면 평균적인 시간이 나오는데 이것이 3인 상수 시간이 걸리게 된다. 따라서 뒤에 요소를 붙이는 것은 배열과 다르게 O(1)시간이 걸린다는 점을 알아두면 좋다.

4. 스택

스택은 프링글스 통을 생각해보자.

포장할때 제일 먼저 들어간 과자는 제일 나중에 나오게 된다. 반대로 제일 나중에 들어간 과자는 제일 먼저 나오게 된다.

이처럼 스택은 가장 마지막으로 들어간 데이터가 가장 첫 번째로 나오는 성질(LIFO, Last In First Out)을 가진 자료 구조이다.

이는 재귀적 함수에 대표적으로 사용되며, 일상적인 상황에서는 뒤로가기를 위한 저장이나 웹 브라우저 방문 기록 등에 쓰인다.

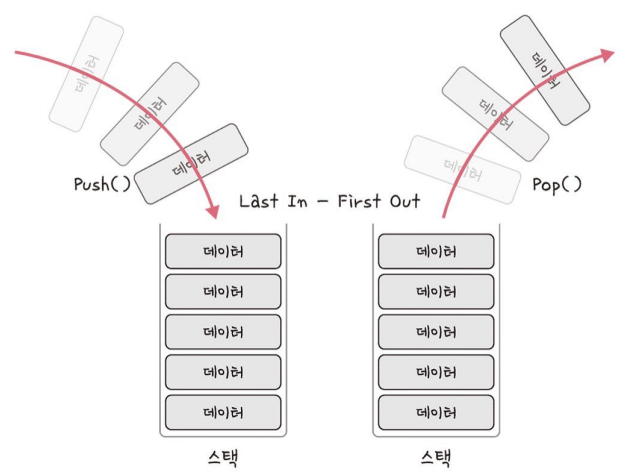
데이터가 삽입되고 나가는 부분을 top 이라고 부른다.
이를 통해서 삽입과 삭제는 O(1)이 걸린다. 탐색은 모두 돌아보면서 데이터를 찾아야 되기 때문에 O(n)이 걸린다.

5. 큐

큐는 우리가 가게 줄을 설 때를 생각해보자.

가장 먼저 온 사람이 가장 먼저 들어간다. 반대로 가장 나중에 온 사람이 나중에 들어간다.

이처럼 큐는 먼저 집어넣은 데이터가 먼저 나오는 성질(FIFO First In First Out)을 지니는 자료구조이다.

큐는 삽입하는 부분인 Back 과 나가는 부분인 Front 가 존재한다. 이 또한 삽입과 삭제는 O(1), 탐색은 O(n)의 시간이 걸린다.
이는 CPU 작업을 기다리는 프로세스, 네트워크 접속을 기다리는 행렬, 캐시 등등에서 많이 쓰인다. 일상생활 속에서는 티켓팅을 할때 접속 대기 순위가 뜨는데 이것이 큐의 예시가 될 수 있다.

마무리

이번 블로깅에선 선형 자료 구조 에 대해 알아보았다. 이 블로깅의 목적은 깊게 배우는 것이 아니라 개발자 대회에 낄 정도의 넒고 얕은 지식을 목표로 하고 있다. 이 블로깅을 통해서 전체적인 선형 자료 구조 에 대해 잡았으면 좋겠다. 그리고 감을 잡았고 좀 더 깊게 배우고 싶다면 이 블로깅의 키워드를 길로 잡아서 하나씩 공부해 나간다면 매우 도움이 될 것이라고 생각한다.