B트리,B+트리, B*트리 개념 정리

오늘은 트리 종류 중 하나인 B트리 시리즈를 정리해보려고 한다.
C로 구현도 해볼 건데, 구현 코드는 다른 포스팅에서 한번 더 정리할 예정이다. 이 포스팅에서는 B트리 개념에 대해서 알고가자.

B트리를 이해하기 전에 먼저 디스크 구조부터 이해하자.

디스크 관련 내용 참조 강의 : https://www.youtube.com/watch?v=aZjYr87r1b8&ab_channel=AbdulBari

• 디스크는 섹터와 트랙으로 나뉘어져있음.
• 섹터는 디스크 영역을 파이처럼 나눔.
• 트랙(레벨)은 디스크의 깊이.
• 블럭은 특정 트랙의 섹터
  • 블럭이 512 바이트로 이루어져있다고 하면, 0부터 511까지 1바이트씩 이루어져있는데, 1바이트는 각자의 주소를 가지고있다.(그걸 offset이라고 한다.)
• 디스크의 특정 지점을 읽으려면 섹터,블럭,offset을 알아야 한다.

데이터가 흐르는 과정 : 메인 메모리에서 프로그램을 돌리려면 데이터를 디스크에서 가져온다 → 결과가 나오면 그걸 디스크에 다시 담는다.

메인 메모리 내의 프로그램이 쓰는 데이터의 집합을 data structure라고 부른다. 데이터를 디스크에서 효율적으로 조직하는걸 DBMS라고 부른다.

예를들어 데이터베이스가 있고, Employee라는 테이블이 있다고 가정하자.

Employee

• eid - 10byte
• name - 50 byte
• dept - 10byte
• section - 8byte
• add -50 byte

총 128byte

• 데이터 베이스에는 100개의 record가 있는데, 1개의 record는 128byte라고 간주한다.
• 블록 1개가 512byte니까 1개의 블럭에 4개의 record를 넣을 수 있는 것이다. 디스크에 100개의 레코드를 넣으려면 총 25개의 블록이 필요하다.
• 이 데이터베이스에서 특정 데이터를 찾으려면 현재 상황으로는 25개의 블록을 하나씩 다 찾아봐야 한다. 운이 없으면 모든 블록을 다 탐색해야 한다.
• 그래서 빠른 탐색을 위해서 indexing을 해야 한다. index에는 eid와 pointer 가 존재한다. 각각의 pointer는 각각의 eid가 속한 레코드를 가리킨다.(레코드 포인터)
• 그러면 index는 어디에 저장되어있는가? index 또한 디스크에 저장되어있다. 단 데이터베이스와 따로 저장되어 있다. 100개의 인덱스를 저장하는데에는 4개의 블록이 필요하다.
• 이제 데이터 탐색을 할 때 인덱스에 접근한다. 인덱스는 4개의 블록에 있으니까 4개의 블록을 탐색한다. 그리고 특정 인덱스에서 포인터를 찾아서 그 포인터가 속한 블록으로 들어간다. 그러면 5개의 블록을 탐색하는거다.

멀티 인덱스

• 만약 레코드가 많아져서 1000개가 됐다고 생각해보자.
• 그럼 인덱스를 구성하는 블록의 개수도 40개로 많아진다. 인덱스 탐색의 효용이 작아진다.

그러면 어떻게 해야 하는가?

• 인덱스를 위한 인덱스를 만들면 된다. 한 개의 블록에 32개의 인덱스가 들어가니까,
• 인덱스 of 인덱스에서 1번째 인덱스는 1번째 블록에 들어갈 진입포인트, 2번째 인덱스는 2번째 블록에 들어갈 진입포인트... 등으로 구성한다.
• 인덱스 of 인덱스는 2개의 블록으로 구성된다.

즉, 총 필요한 블록은 92 블록이다.

• 인덱싱 of 인덱싱이 깊어지면 레벨이 생길 것이다. 그걸 트리형태로 표현하면 그게 B 트리의 원형이 된다. (이런 인덱싱 관리를 매번 수동으로 할 수 없으니 자동으로 self manage high level indexing을 하려고 한게 B트리이다.)

우선, B Tree를 알기전에 M-way Search Tree를 알고가자.

M-way search tree(MST)

이진 탐색 트리의 특성을 띄어서 자식 노드를 구성할 때 작은 건 왼쪽, 큰건 오른쪽에 오는 트리이다. 한 개의 키에 2개의 자식 노드가 있다.

MST는 한개의 노드에 여러개의 키가 있을 수 있다. 자식 노드에도 여러 개의 키가 들어갈 수 있다.

예를 들어 한 개의 노드에 2개의 키가 들어가면, 자식 포인터는 3개를 가질 수 있다. 이걸 3-way search tree라고 한다.

4-way search tree 같은 경우 3개의 key가 들어가고 4개의 자식을 가질 수 있다.

노드 구성1 ⬇️

예시1 : child pointer | key1 | child pointer | key2 | child pointer | key3 | child pointer

이 구성을 가지고 멀티 인덱싱 용도로 응용해보자. 결국 인덱싱은 레코드를 포인팅해야하니까 레코드 포인터도 필요하다.

노드 구성2 ⬇️

예시2 : child pointer | key1 | record pointer | child pointer | key2 | record pointer | child pointer | key3 | record pointer | child pointer

B Tree

M-way tree의 차수가 많아지면 트리의 높이도 n이된다. 커지면 비효율적이게 되는 것이다. 그래서 B트리라는 걸 만들어서 규칙이 있는 m-way search tree를 구상했다.

[규칙]

• 루트를 제외한 모든 노드는 ⌈m/2⌉ 만큼의 자식 포인터를 가져야 한다. 차수가 10이면 한 개의 노드가 자식 포인터를 최소 5개 가져야한다.
• 루트 노드는 최소 2개의 자식 포인터를 가져야 한다.
• 모든 리프 노드는 똑같은 레벨이어야 한다.
• creation process는 bottom-up이라고 생각하면 된다.

Creation process

데이터가 10,20,40,50이 있다. 차수는 4이다.(= 노드의 데이터는 3개 들어갈 수 있다.)

• 처음 노드에 10,20,40 키를 넣는다.

• 이제 50을 넣으려고 하는데 노드에 자리가 없다. 그래서 노드를 하나 옆에 추가하고, 50을 거기 넣는다.

• 그리고 1번째 노드에서 40을 빼서 부모 노드로 만든다.

• 40의 왼쪽 자식 노드는 (10,20)이 되고, 오른쪽 자식 노드는 (50)이 된다.

  40
  ↙️ ↘

(10,20) (50)

• 이렇게 계속 위로 가기 때문에 bottom-up creation process이다.

B Tree에서 레코드 포인팅 하는법

결국 노드들은 데이터베이스의 레코드를 가리켜야 한다. B 트리에서는 각 노드마다 레코드 포인터가 존재한다.

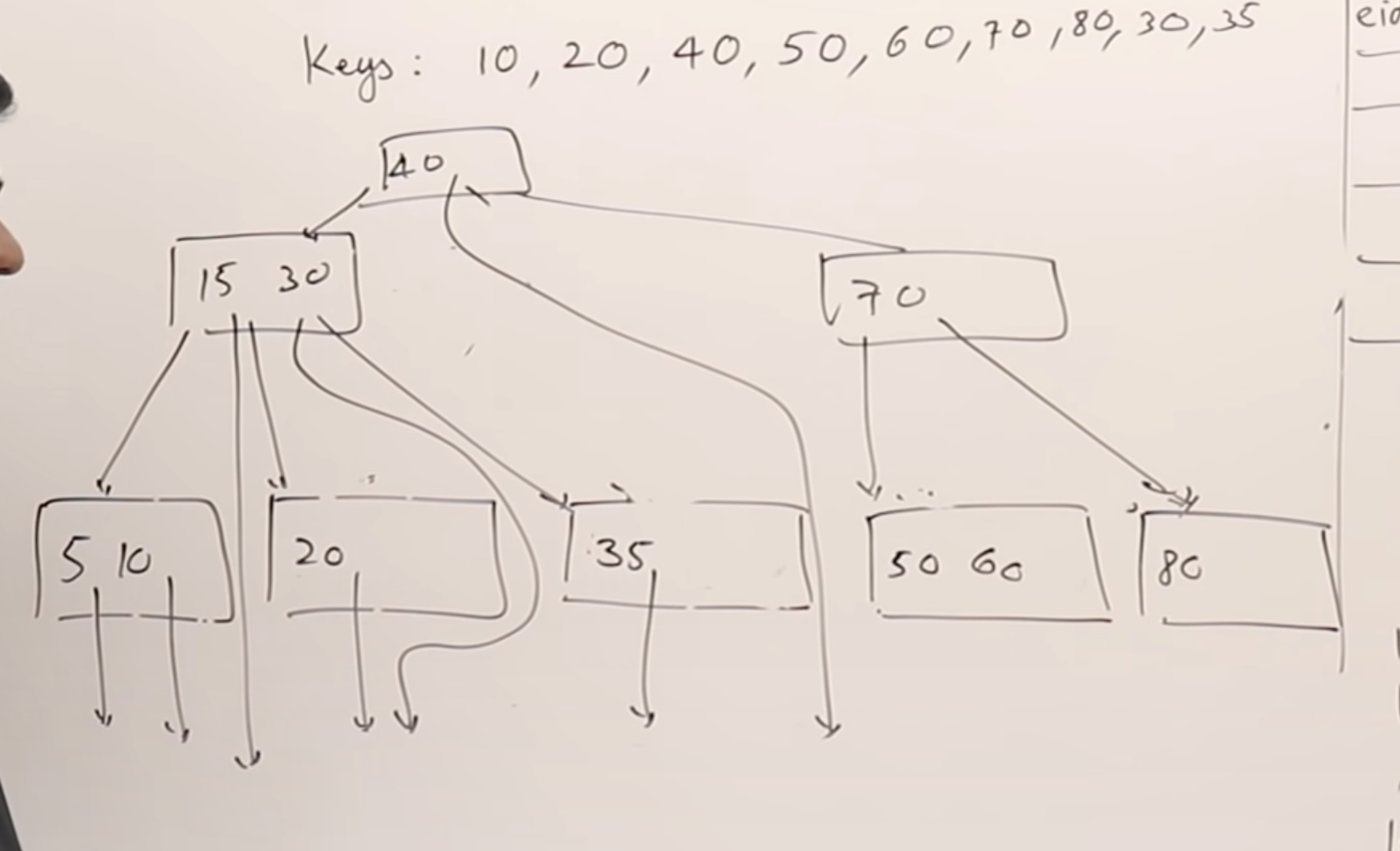
B+ Tree

• B tree는 모든 노드에 레코드 포인터를 가지지만, B+ Tree는 오직 리프 노드에서만 레코드 포인터를 가진다. 그래서 대신에 리프 노드에 모든 키들이 존재해야 한다.(부모노드에도 존재한다.)
• 모든 리프노드는 왼쪽에서 오른쪽으로 연결되어있다. (연결리스트 활용)

---

추가 개념 정리

B-트리

이진트리의 확장된 버전으로 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 m원 탐색 트리 자료구조이다.

노드의 자식 노드 레벨 규칙을 두어 전체적으로 트리의 균형을 유지하기 때문에 기본적인 m원 탐색 트리보다 향상된 탐색 성능을 가지고 있다고 볼 수 있다. B트리의 특징을 열거하면 아래와 같다.

• 노드가 삽입되거나 삭제될 때, 내부 노드는 자식 노드의 수를 만족시키기 위해 분리되거나 혹은 다른 노드와 합쳐진다.
• 루트와 잎 노드를 제외한 트리의 노드는 최소 ⌈m/2⌉개의 서브트리를 가져야 한다. 여기서 m은 차수를 의미하는데 예를 들어 m이 3이면, 내부노드는 최소 ⌈3/2⌉ = 2개의 서브트리를 가져야 한다는 뜻이다. 차수가 3이기 때문에 각각의 노드는 2개의 키를 가진다.
• 루트 노드는 최소 2개의 자식(서브 트리)을 가져야 한다.
• 트리의 모든 잎 노드는 같은 레벨에 있어야 한다. 이는 내부 노드에 있는 자식 노드의 수를 최대화함으로써 트리의 높이는 감소하며, 균형 맞춤은 덜 발생하고, 효율 증가를 가져다 준다.
• 모든 삽입은 잎 노드에서 시작해야 한다. 삽입을 할 때는 삽입할 위치를 찾기 위해 노드를 왼쪽에서 오른쪽으로 탐색하며 들어갈 자리를 찾는다. 분리가 필요하면, 노드를 2개로 분리하고 키값과 포인터를 분리한 노드에 분배한다.
• 분배 시 중간 값을 가지는 노드는 부모 노드에 삽입한다.
• 삭제를 할 때는 먼저 삭제할 키값을 가지고 있는 노드를 찾아야 한다. 그 노드가 잎 노드일 경우, 키값을 삭제하고 필요 시 노드들을 재배열한다.
  • 그 노드가 내부노드일 경우, 키값을 삭제하고 잎 노드에서 삭제된 자리에 올 키 값을 옮긴다. 삭제된 자리로 옮길 잎 노드가 정해진 개수의 키 값을 갖지 않으면 트리를 재배열 한다.

B*트리

B-트리를 변형시킨 트리로서 공집합이거나 높이가 1 이상인 m원 탐색 트리이다.(m은 차수).

루트 노드가 아닌 노드는 노드의 2/3 이상이 채워져야 하는 특징이 있다. 루트노드가 가지는 자식노드의 갯수 범위는 2 ≤ x ≤ 2⌊(2m-2)/3⌋ +1 (x는 개수).

• 루트 노드와 잎노드가 아닌 노드는 최소 ⌈(2m-1)/3⌉ 개의 자식 노드를 가져야 한다. 차수가 m이기 때문에 잎노드가 아닌 노드는 포인터가 m개, 키 개수는 m-1개를 갖는다.

B*트리 또한 노드 삽입/삭제가 가능한데, 삽입 시 노드가 꽉 차더라도 바로 분리하지 않고, 키값과 포인터를 재분배하여 형제 노드로 이동시키는 구조를 갖고 있다. 만약 형제노드가 꽉 차있는 경우 노드를 분리한다.(2개 → 3개) 분리한 노드는 노드의 약 2/3가 차있어야 한다. 새로운 노드를 위해 새 메모리를 할당하는게 아니라 기존에 있는 노드로 이동시키기 때문에 '분리'보다 비용이 적게 든다.

삭제는 B-트리의 방법과 동일하지만, 삭제될 자리로 옮길 잎 노드가 정해진 개수의 키 값을 갖지 않을 때 형제 노드로부터 키 값을 재분배한다. 재분배 할 수 없는 경우 노드를 합친다(3개 → 2개).

B+트리

B-트리의 특징을 가지고 있지만, 모든 키 값들이 잎 노드에 정렬되어있는 트리 구조이다. 잎 노드를 순차적으로 연결하는 포인터 집합을 가지고 있다.

이런 특성 때문에 인덱스 된 순차 파일을 구성하는데 사용된다. 순차 처리 시 포인터를 이용할 수 있기 때문에 키 값을 모두 일일이 비교하지않고 다음 데이터에 접근해서 처리할 수 있기 때문이다.

따라서 모든 키 값은 잎 노드가 가지고 있으며, 키 값의 실제 데이터 주소도 잎 노드만 가지고 있다.

• B-트리와 동일하게 루트와 잎 노드를 제외한 트리의 노드는 최소 ⌈m/2⌉개의 서브트리를 가져야 한다. 루
• 트 노드 또한 최소 2개의 서브트리를 가져야 한다.
• 노드에 빈 자리가 있으면 삽입을 하고, 노드에 빈 자리가 없으면 노드를 분리하고 중간 값을 가진 노드를 부모 노드에 삽입한다.
• 삭제 시에는 잎 노드에서만 키 값을 삭제한다.
  • 만약 삭제로 인해 잎 노드가 없어지게 되면 형제 노드를 확인해 형제 노드를 재분배해 작은 키 값을 삭제한 노드 위치에 둔다.
  • 인접 형제 노드가 재분배 할 수 없으면 삭제할 키 값의 잎 노드와 형제노드를 병합한다.

B+ 트리의 검색,삽입,삭제

일반적인 노드 구조

n-1개의K와n개의 포인터 P(팬아웃)로 구성.  (Pi는 Ki를 가지는 레코드(i = 1 ~ n-1))

P1 | K1 | P2 | ··· | Pn-1 | Kn-1 | Pn

노드 안의 K값은 정렬된 순서로 유지. 한 노드에 저장되는 최대 포인터의 개수는 n.

검색

검색 연산은 순차 세트에 도달하여 K에 해당하는 레코드 포인터를 획득하는 것으로 종료.

예 : K값 JPL15에 대한 검색 연산 시행

• n = 3, 탐색 시점의 노드는 Y

1. Y(루트노드)를 조사해서 JPL15과 같거나 JPL15보다 큰 K 중 가장 작은 K를 찾음.
2. K가 해당 노드에 아무것도 없기때문에 오른쪽 포인터를 따라가게 됨
3. 중간 노드 진입, JPL15보다 큰 K 중 가장 작은 K 탐색
4. 해당 K = POC12, POC12의 왼쪽 포인터를 따라감
5. 단말노드 진입, 해당 노드의 처음부터 살펴서 JPL15가 있는지 확인
6. JPL15가 존재하므로 JPL15의 왼쪽 포인터에 접근해 블록에 담긴 레코드 탐색
7. 5번 시점에 해당 노드가 단말노드가 아니면 1부터 반복.
   

삽입

레코드 삽입은 새로운 K에 대한 인덱스 엔트리를 반영하는 과정.

삽입 시 해당 노드에서 유지해야 할 K와 포인터 수가 증가하는지에 따라 노드 분할 여부가 나뉨.

예시 :  n = 3, K값은 ‘GGL12’만 존재. GGL22삽입 요청.

1.GGL22이 속해야 할 단말 노드 탐색. 새 K값을 저장해야 할 노드에 빈 공간이 남아있는지 탐색.

2.루트노드에 공간이 남아있으므로 삽입. 분할은 발생하지 않음.

3.노드 내의 K들의 순서 유지.

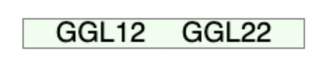
4.GGL50을 추가 삽입 요청

5.루트 노드에 저장 공간이 없으므로 분할 진행.(이유 : n= 3, 가능한 K 수 = 2)

6.분할 전 순서를 유지한 K 기준으로 부모 노드에 GGL22를 올림. (n은  3이기 때문에 1번째 index(2번째 K))

부모노드 선택 :

• ⌈n/2⌉=t 라고 정의. / t는 0부터 시작
• n 이 홀수 : 상위에 t-1 번째 index
• n 이 짝수 : 상위에 t 번째 index

자식 포인터 연결  :

• 부모노드의 왼쪽 자식노드는 부모노드보다 작게 연결 되어야 함.
• 오른쪽 자식노드는 부모노드와 같거나 크게 연결 되어야 함.

6. GGL22보다 작은 GGL12가 왼쪽 자식노드(단말노드). GGL22와 GGL50은 오른쪽 자식노드(단말노드)
   

7.GGL70, JPL15를 차례대로 삽입

8.JPL15 추가 시 부모노드에 추가할 공간이 없기 때문에 부모노드 레벨에서 분할 수행.(중간노드 생성, 루트노드는 GGL50)

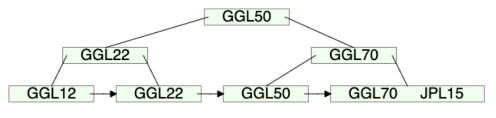
삭제

레코드 삭제는 삭제할 K와 포인터를 포함하는 단말노드를 검색하고 해당 K와 포인터를 삭제하는 과정.

예 : GGL70 삭제

1.GGL70 검색 후 해당 K, 연관된 포인터 삭제

2.삭제한 엔트리의 오른쪽에 있는 엔트리들은 빈 공간이 발생하지 않게 왼쪽으로 이동.

3. GGL22, GGL24 차례대로 삭제

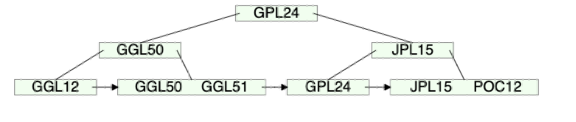
4.GGL12삭제

5.GGL12이 속한 노드가 공백상태가 됨 & K 개수도 ⌈(차수-1)/2⌉개 보다 적어짐.

6.다음 이웃 단말 노드인 GGL50, GGL51의 키를 재분배, JPL15의 부모노드를 재분배. (2번 과정 포함)

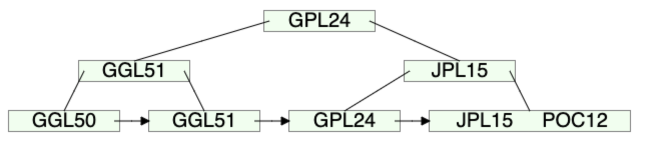
7.GPL24, POC12, JPL15를 차례대로 삭제

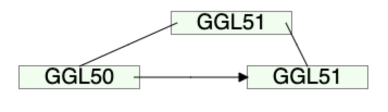
8.JPL15의 다음 이웃 단말 노드가 ⌈(n-1)/2⌉ 개보다 K값이 적음. GGL51과 이웃 단말 노드와의 병합.