최강 증가 부분 수열(LIS) 알고리즘

최장 증가 부분 수열(LIS) 알고리즘

---

최장 증가 부분 수열(Longest Increasing Subsequence)이란?

원소개 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중, 각 원소가 이전 원소보다 크다는 조건을 만족하고, 그 길이가 최대인 부분 수열을 최장 증가 부분 수열이라고 한다.

일반적으로 LIS의 간편한 방법에는 DP가 있다.

for (int k=0; k<n; k++){
	length[k] = 1;
	for (int i=0; i<k; i++){
		if(arr[i] < arr[k]){
			length[k] = max(length[k], length[i] + 1);
		}
	}
}

위의 코드에서 length[I]는 i번째 인덱스에서 끝나는 최장 증가 부분 수열의 길이를 의미한다.

업데이트하는 기준은,

1. i번째 인덱스에서 끝나는 최장 증가 부분 수열의 마지막에 arr[k]를 추가했을 때의 LIS 길이와
2. 추가하지 않고 기존의 length[k]값
3. 둘 중에 더 큰 값으로 length[k]값을 업데이트 한다.

허나 위 알고리즘의 시간복잡도는 O(n^2)이다. 굉장이 비효율적이라고 할 수 있다.

이분탐색을 활용한 LIS

LIS의 형태를 유지하기 위해 주어진 배열의 인덱스를 하나씩 살펴보면서 그 숫자가 들어갈 위치를 이분탐색으로 탐색해서 넣는다.
이분탐색은 일반적으로 시간복잡도가 O(logn)으로 알려져 있으므로, 위의 문제를 O(blogs)의 시간복잡도로 해결할 수 있게 된다.

int n;
int arr[40001];
int lis[40001];

int binarySearch(int left, int right, int target){
	int mid;
	while(left<right){
		mid = (left+right)/2;
		if(lis[mid] < target){
			left = mid+1;
		}
		else{
			right = mid;
		}
	}
	return right;
}

int main(){
	int n;
	cin >> n;
	for(int i=0; i<n; i++){
		cin >> arr[i];
	}

	int j=0;
	lis[0] = arr[0]
	int i=1;
	while(i<n){
		if(lis[j] < arr[i]){
			lis[j+1] = arr[i];
			j+=1
		}
		else{
			int pos = binarySearch(0,j,arr[i]);
			lis[pos] = arr[i];
		}
		i+=1;
	}
	cout<< j+1;
	return 0;
}

위의 코드는 단순히 LIS의 길이를 구하는 방법이다.
만약 실제 LIS를 구하고 싶다면 다음과 같은 방법을 사용해야 한다.

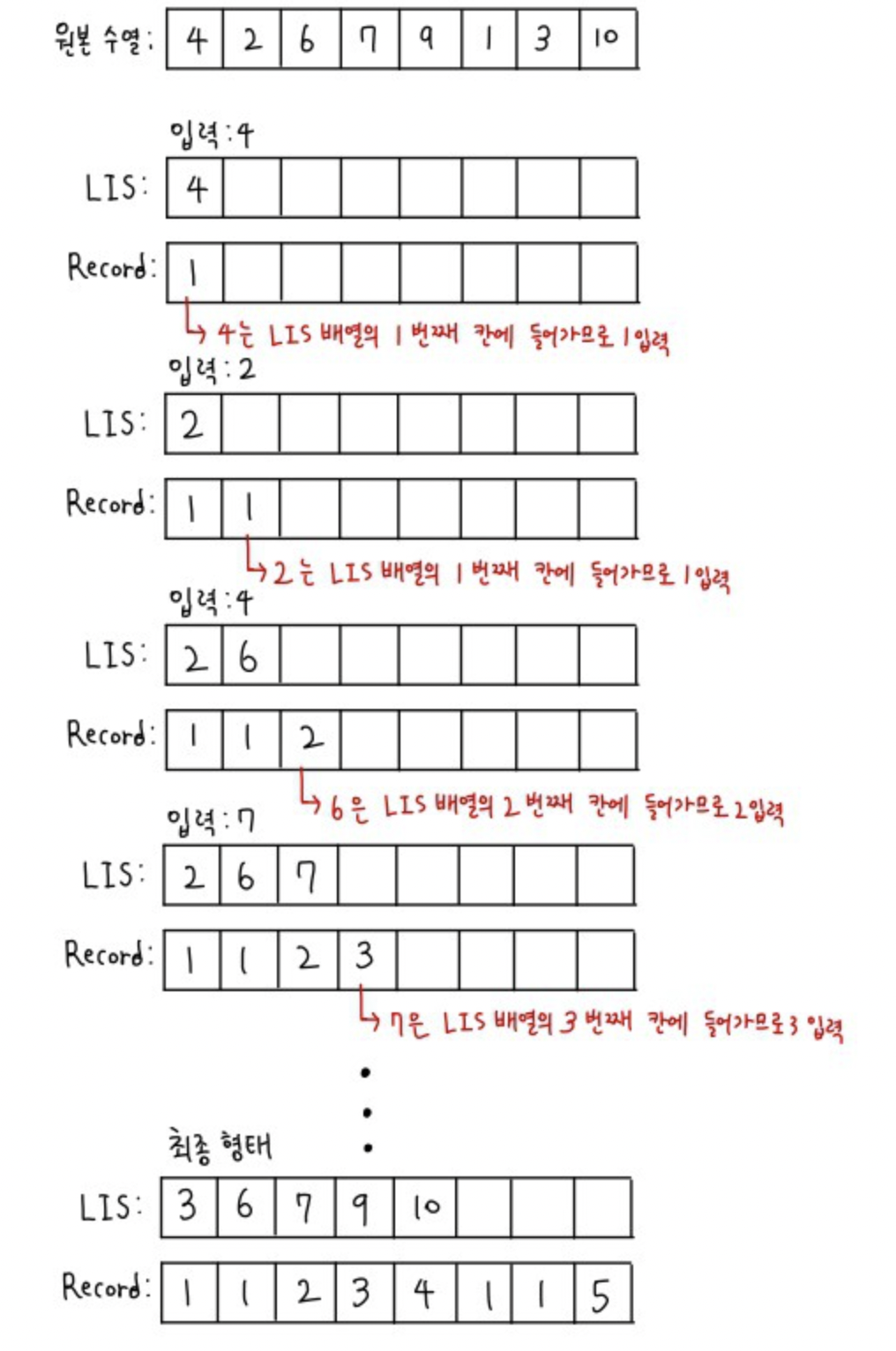
1. 각 수가 LIS 배열에 들어갈 때 몇번째 인덱스에 들어가는지를 record라는 리스트에 저장을 한다.
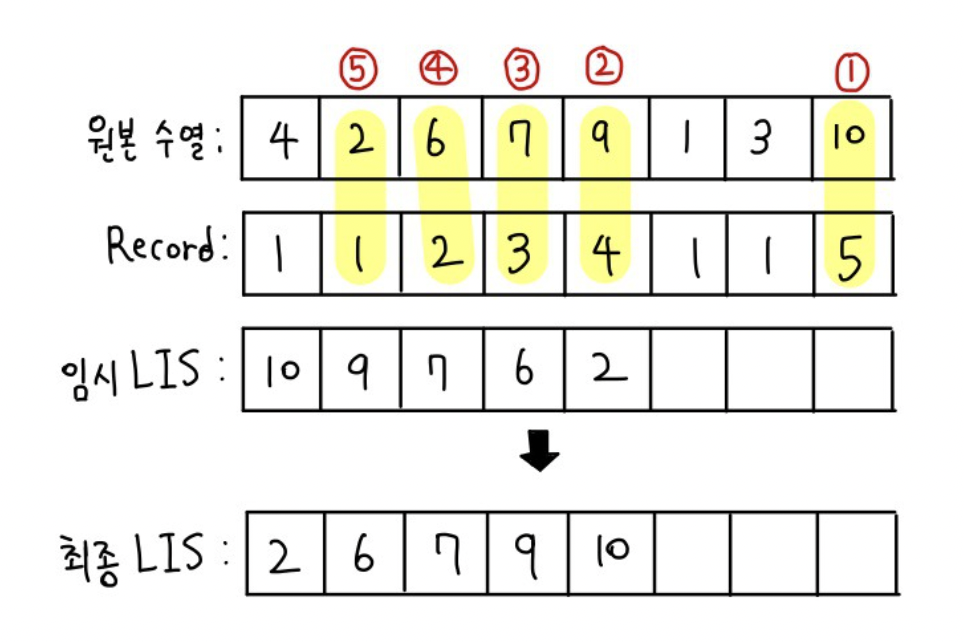
2. 이후에 record가 다 차면 record의 최대값으로부터 역순으로 순회하여 그 인덱스에 해당하는 값을 LIS Result에 저장한다.
3. LIS Result를 오름차순으로 정렬한다.
4. 실제 LIS가 완성된다.

REFERENCE

---

이미지 출처 : https://yhwan.tistory.com/21