최소 공통 조상 LCA

문제

https://www.acmicpc.net/problem/11438

개요

트리의 최소 공통 조상이란 Lowest Common Ancestor을 의미하며 LCA로 알려져 있다.

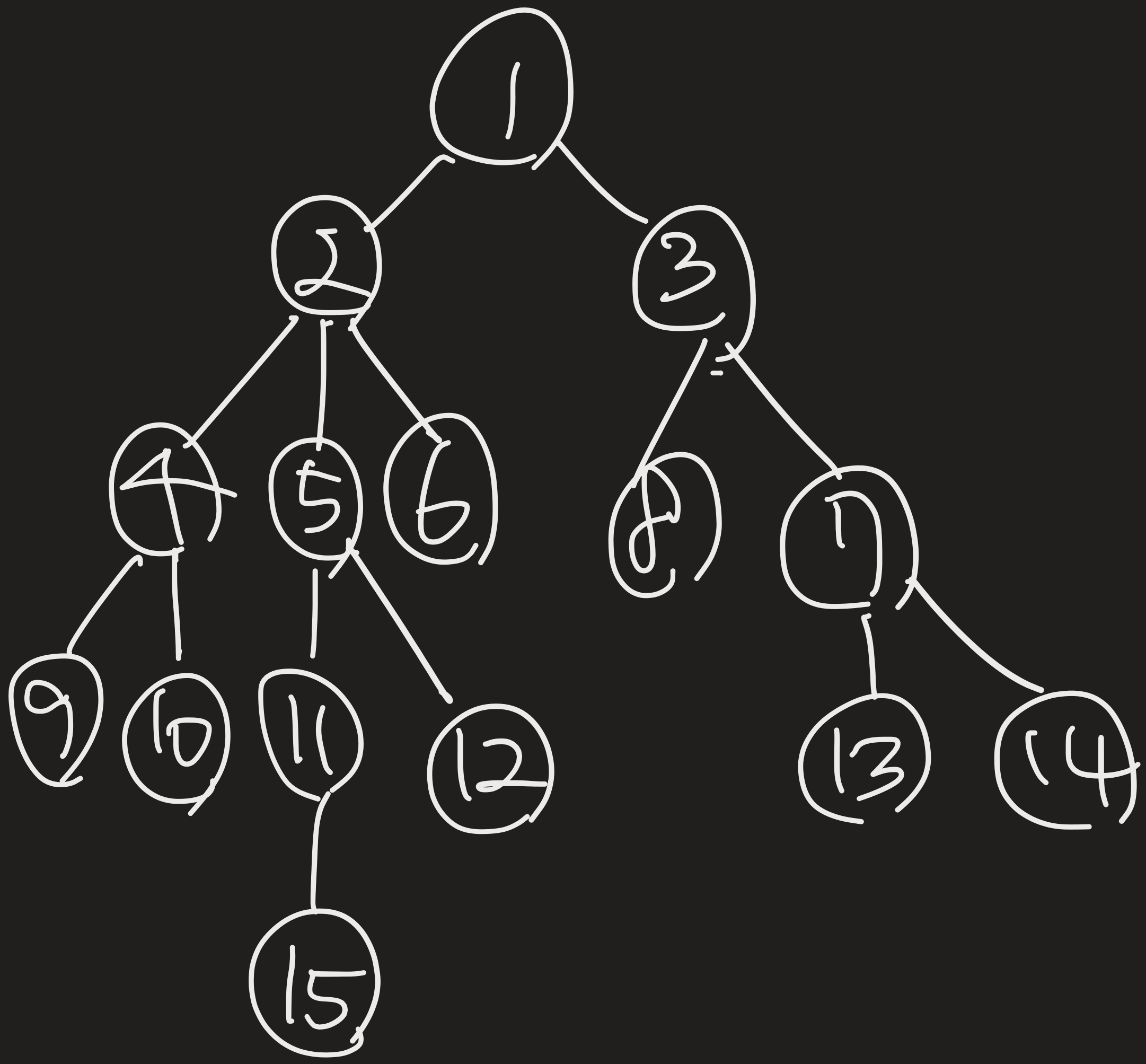
예를 들어 위와 같은 트리에서는

LCA(2, 3) = 1
LCA(6, 7) = 1
LCA(15, 11) = 11 이다.

풀이

LCA를 찾는 방법은 Linear하게 $O(N)$만에 찾는 방법과 $O(logN)$만에 찾는 방법이 있다.
물론 노드의 개수가 많으면 많을 수록 $O(logN)$을 쓰는 것이 훨씬 효율적이고 그 방법을 써야만 한다.
이 글은 $O(logN)$만에 찾는 방법을 설명하는 것에 중점을 둔 글이므로 Linear하게 찾는 방법은 간단히 설명하고 넘어가겠다.

LCA를 찾는 Linear한 방법 :
1. 두 노드의 깊이를 동일하게 맞춰준다.
2. 같은 깊이에서 선형적으로 부모를 타고 올라간다.
3. 부모 노드의 번호가 같을때 그 번호가 LCA이다.

이어서 $O(logN)$에 찾는 방법을 알아보자.
$O(logN)$ 만에 찾는 방법에서도 두 노드의 깊이를 동일하게 맞춰주는 과정을 거친다.
단, Linear한 방법과는 달리 $O(logN)$ 만에 깊이를 동일하게 맞출 수 있다.

예를 들어 두 노드의 깊이 차이(depthDiff)가 15라고 하자.
15은 이진수로 1111(2) 이다.그러므로 1111(2) 의 어느 자리에서 1이 등장하는지 파악하고 1이 등장하는 위치의 값만큼 노드를 이동시키는 계산을 해주면 된다.

이 개념은 15 = 1+2+4+8 로 표현하여 15를 계산하는 수행을 4번만에 완료하는 방법과 같은 맥락이다.

이 과정을 수행하기 위해서는 Sparse Table이 필요하다.
Sparse Table은 각 행이 노드의 번호를 의미하고 각 열은 2의 지수를 의미한다.
따라서 다음의 정보를 담은 2차원 Table을 만들 수 있다.

sparseTable[i][k] = i번 노드의 $2^k$번째 부모노드
ex) sparseTable[i][0] = i번 노드의 $2^0$번째 부모노드 = i번 노드의 1번째 부모노드

Tip : 모든 자연수는 2의 거듭제곱으로 표현할 수 있다.
따라서 어떤 노드의 모든 n번째 부모 노드의 정보를 Sparse Table로 알아낼 수 있다.

풀이의 전체적인 흐름은 다음과 같다.

1. 입력값을 통해서 트리를 전처리 해준다.
2. 전처리 해줄 때는 dfs, bfs 둘다 상관 없다. 단 현재 노드의 부모노드를 sparseTable[node][0]에 저장해주면서 진행한다.
3. 트리에서 노드의 깊이를 depth[node]에 저장해주면서 진행한다.
4. sparseTable[n][k] = sparseTable[ sparseTable[n][k-1] ][ k-1 ] 를 이용해서 SparseTable을 채워준다.
5. 입력 받는 쿼리(노드1, 노드2)에서 두 노드의 깊이 차이를 계산한다.
6. 더 깊은 노드를 logN만에 더 얕은 깊이와 동일한 깊이의 새로운 노드로 끌어올릴 수 있다.
7. 이제 두 노드의 깊이가 동일하므로 spaseTable을 이용해서 LCA를 찾는다.

위 흐름에서 핵심은 4번 과정이다. 아래 그림을 보면서 이해해보자

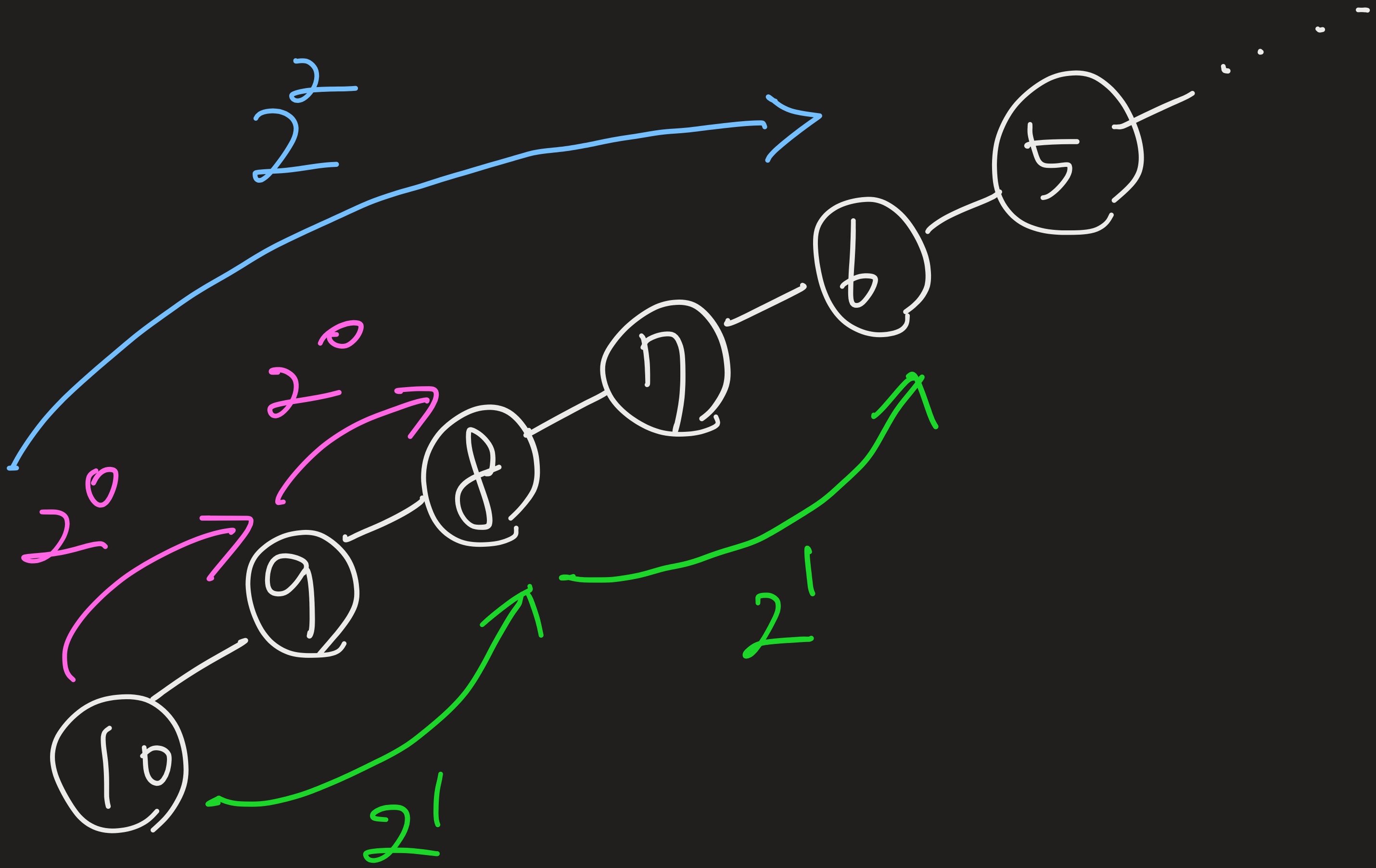
10번 노드에서 8번노드는 $2^1$ 번째 부모노드이다.
8번 노드는 9번노드에서 $2^0$ 번째 부모노드이다.
---> dp[10][1] == dp[ dp[10][0] ][ 0 ]

10번노드에서 6번 노드는 $2^2$ 번째 부모노드이다.
6번 노드는 8번 노드에서 $2^1$ 번째 부모노드이다.
---> dp[10][2] == dp[ dp[10][1] ][ 1 ]

즉 sparseTable[n][k] = sparseTable[ sparseTable[n][k-1] ][ k-1 ]이다.

이제 서로 다른 깊이의 노드를 logN만에 동일하게 맞추는 방법을 이해해보자.

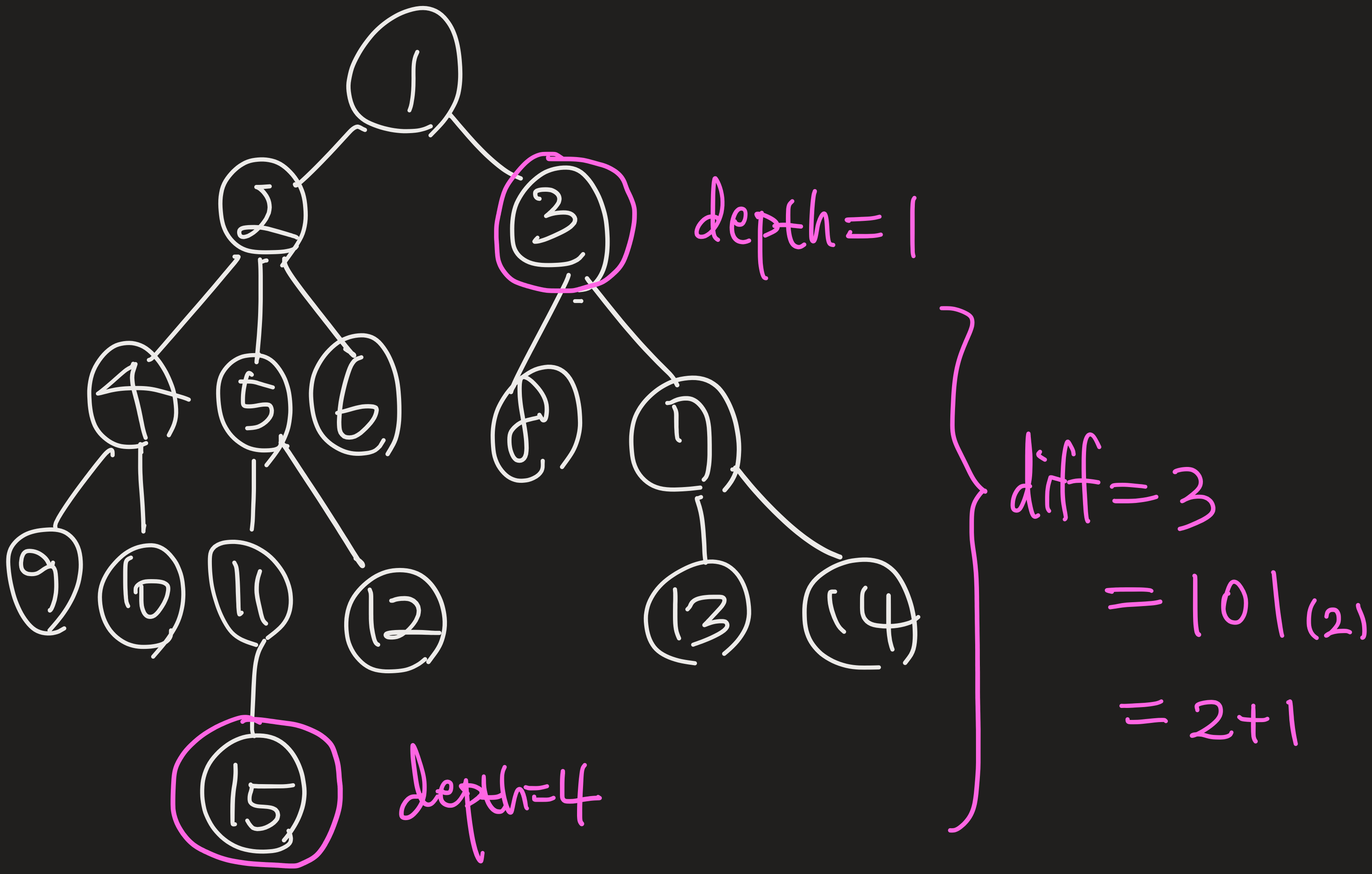
위 그림에서 15번 노드와 3번 노드의 LCA를 찾으려고 한다.

먼저 깊이 차이 diff=3을 계산하고 이를 이진수로 계산해서 $ceil(log3)$만에 수행할 수 있다. 위에서 15 = 1+2+4+8의 방법으로 계산하는 맥락과 동일하다.

정리하면 더 깊은 노드에서 $log(diff)$만에 같은 깊이의 노드로 맞춰줄 수 있다는 말이다.

마지막으로 같은 깊이의 두 노드에서 LCA를 찾는 과정을 정리해보자

sparseTable[node1] 과 sparseTable[node2] 에서 상위 MAX 부모노드 부터 0까지 서로 비교한다.
여기서 MAX는 $2^{MAX}$ == 트리의 전체 깊이의 MAX이다.
0은 $2^0 = 1$ 번째 상위 부모노드를 의미한다.

해당 위치의 노드가 아예 존재하지 않을 경우는 sparseTable[i][k] == 0 이다.

MAX 부터 0까지 비교하는 과정에서 두 노드의 부모노드가 서로 다르다면 node1과 node2를 해당 단계에서 계산된 부모노드로 새롭게 갱신하고 이어서 작업한다.

부모노드가 서로 같다면 node1과 node2를 유지한다.

0까지 비교하고 나서 정답은 sparseTable[node1][0]을 출력한다.(마지막에 서로 다른 두 노드의 첫번째 부모노드가 LCA이다.)

이 방법이 가능한 이유에 대해서 설명하고 글을 마친다.

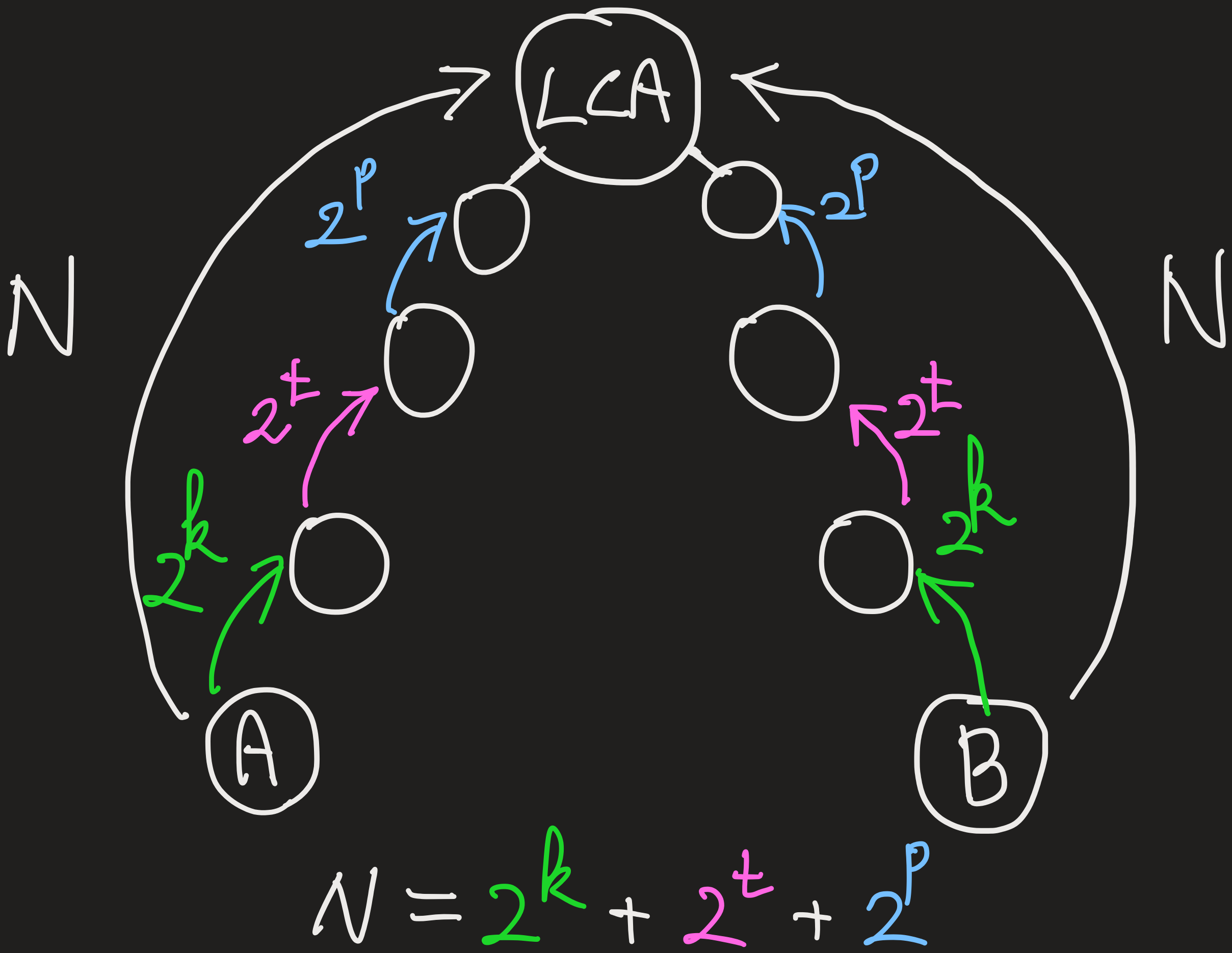
핵심은 node1과 node2를 갱신하는데에 있다.
초기 두 노드에서 $2^k$ 번째 위에 있는 부모노드가 서로 값이 다르면 초기 두 노드를 갱신해준다.
이 때 처음 찾은 두 부모 노드는 LCA와 초기 두 노드까지 떨어진 거리에서 가장 큰 portion을 차지한다.

$15 = 2^3 + 2^2 + 2^1 + 2^0$ 으로 표현할 때 처음 찾게되는 부분은 $2^3$이라는 의미이다.
이제 $2^3$에 $2^2$를 더해서 $2^3 + 2^2 == 12$를 찾아주고
한번 더 진행하여 $2^3 + 2^2 + 2^1 == 14$까지 찾아줄 수 있다.
결과적으로 계속 갱신을 거듭해서 $2^3 + 2^2 + 2^1 + 2^0 == 15$ 를 찾아주는 방식이다.

따라서 마지막에 LCA를 찾는 for loop에서 i인자는 MAX~0으로 감소하는 식으로 진행되고 이는 LCA와 초기 두 노드까지 떨어진 거리를 2의 거듭제곱의 합으로 표현할 때 지수의 값을 나타낸다.

아래 그림을 보면서 이해해보자.

코드

import sys
from math import log2
sys.setrecursionlimit(10**5)
In = lambda: sys.stdin.readline().rstrip()
MIS = lambda: map(int, In().split())

# https://alphatechnic.tistory.com/23 와 같은 실수를 함 (sparseTable 채우는 부분)

def init():
    N = int(In())
    tree = [[] for i in range(N + 1)]
    for n in range(N - 1):
        u, v = MIS()
        tree[u].append(v)
        tree[v].append(u)
    depth = [0] * (N + 1)
    MAX = int(log2(N)) + 1
    dp = [[0] * (MAX + 1) for i in range(N + 1)] #sparseTable 부분
    M = int(In())
    return N, tree, depth, dp, M, MAX


def dfs(cur, pre, d):
    for nxt in tree[cur]:
        if nxt == pre: continue
        depth[nxt] = d + 1
        dp[nxt][0] = cur
        dfs(nxt, cur, d + 1)


def sparseTable():
    for j in range(1, MAX + 1):
        for i in range(1, N + 1):
            dp[i][j] = dp[dp[i][j - 1]][j - 1]


def findDepthDiff(u, v):
    return (depth[u] - depth[v], v, u) if depth[u] > depth[v] \
        else (depth[v] - depth[u], u, v)


def moving(depthDiff, mx):  # 깊이가 더 깊은 노드를 대상으로 깊이를 맞춰주는 작업
    j = 0
    jj = 1 << j
    while jj <= depthDiff:
        if depthDiff & jj:
            mx = dp[mx][j]
        j += 1
        jj = jj<<1
    '''
    diff = 8, 1000(2)
    j = 0, jj = 1
    j = 1, jj = 2
    j = 2, jj = 4
    j = 3, jj = 8 -> mx = dp[mx][3]
    '''
    return mx


def movingWith(mn, mx):  # 깊이는 같고 노드가 다를 경우 동시에 높이를 조절하면서 LCA 탐색
    for j in range(MAX-1, -1, -1):
        if dp[mx][j] == dp[mn][j]: continue
        if dp[mx][j] != 0 and dp[mx][j] != dp[mn][j]:
            mx = dp[mx][j]
            mn = dp[mn][j]
    ans = dp[mx][0]
    return ans


N, tree, depth, dp, M, MAX = init()
dfs(1, 0, 0)
sparseTable()

for m in range(M):
    u, v = MIS()
    depthDiff, mn, mx = findDepthDiff(u, v)
    mx = moving(depthDiff, mx)
    ans = mx
    if mn != mx:
        ans = movingWith(mn, mx)
    print(ans)