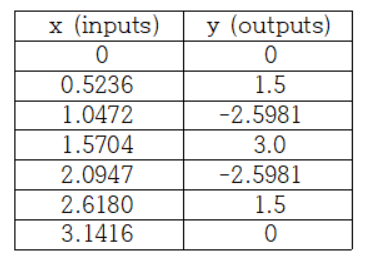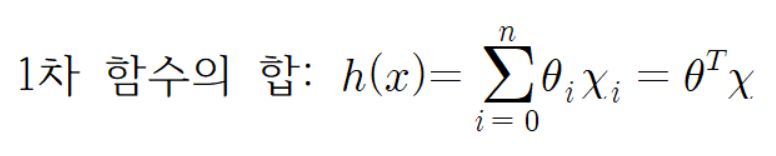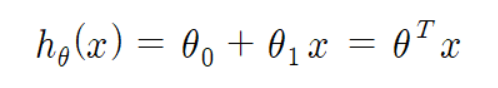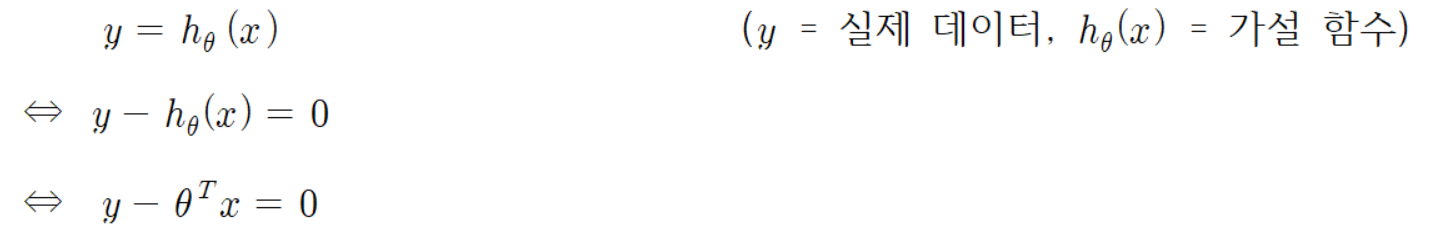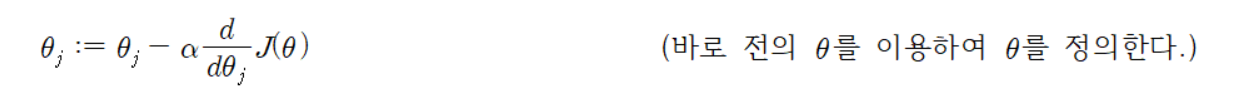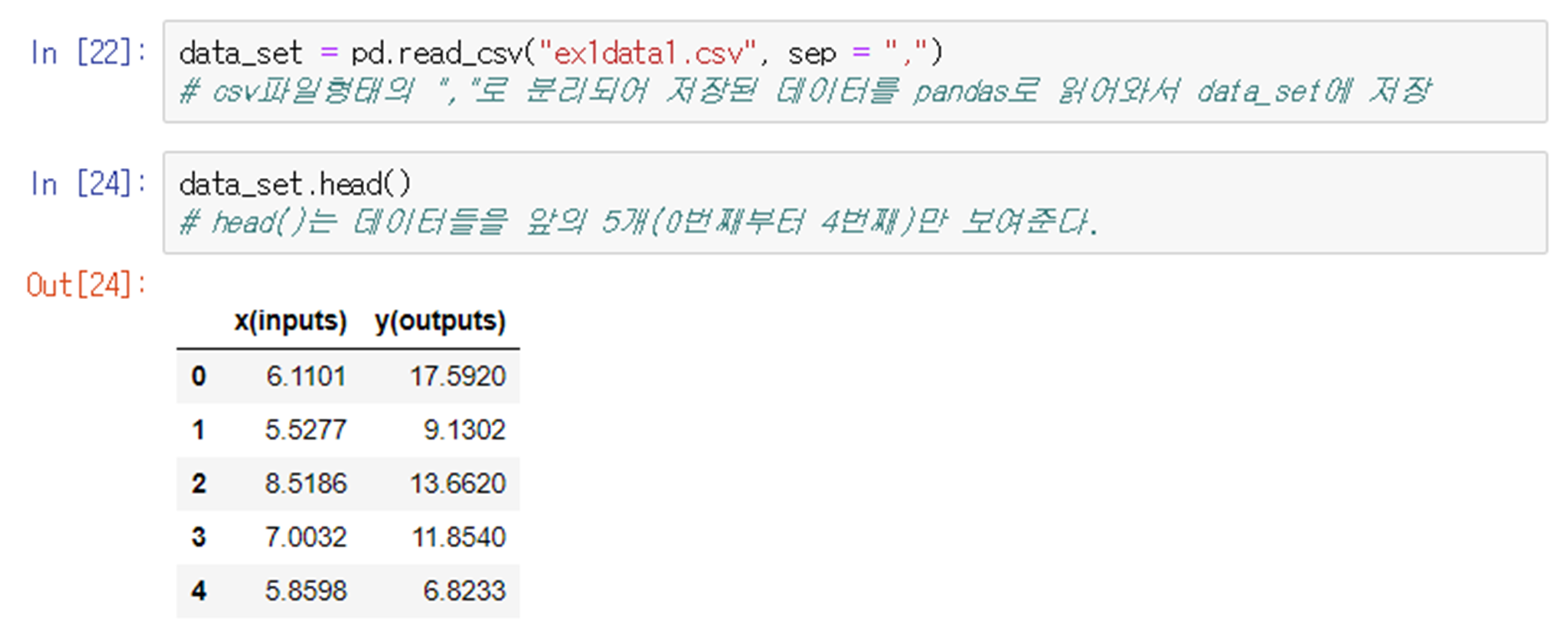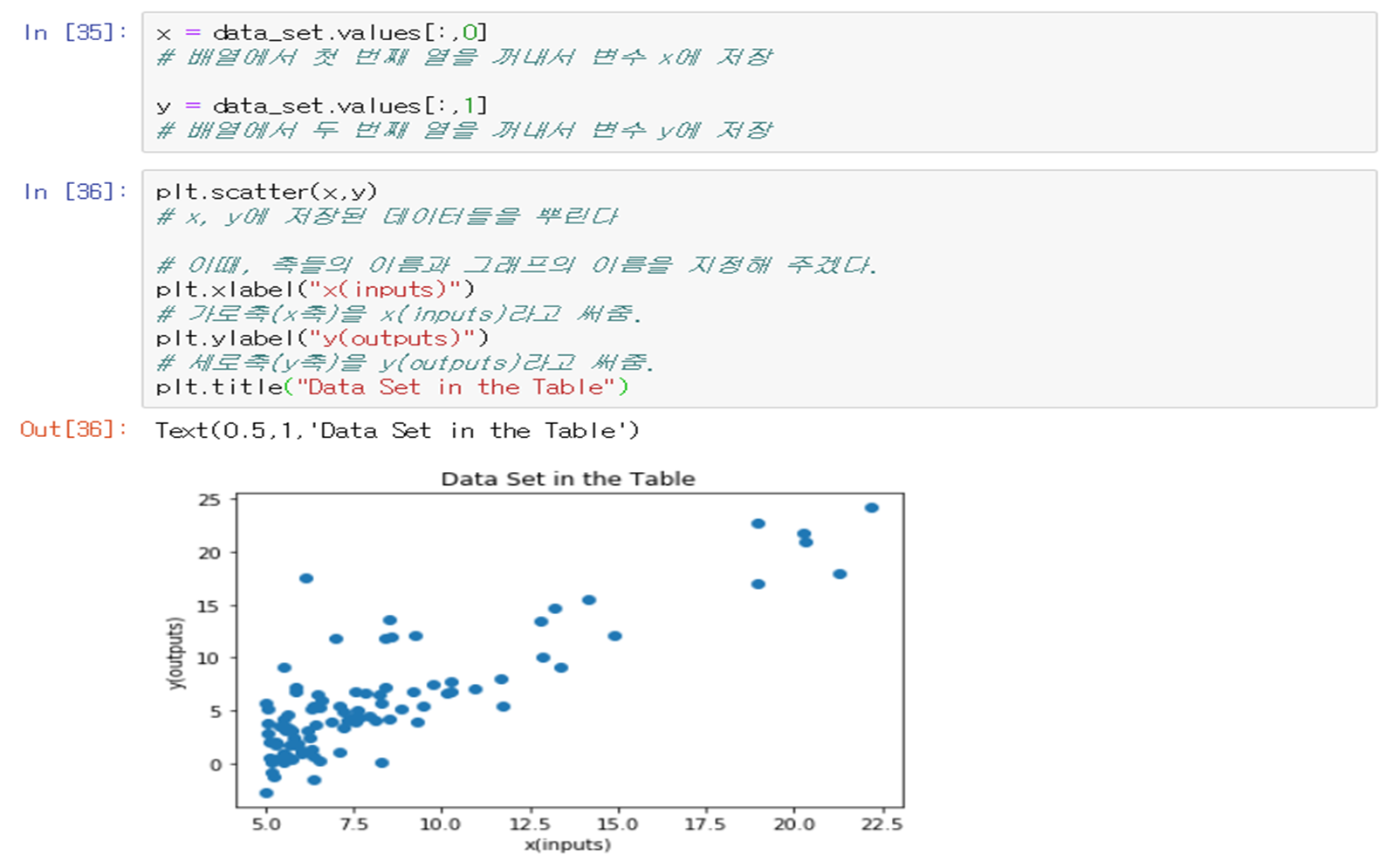
위의 표를 보면 입력 값 x에 대해 y값이 출력 되는 형태의 데이터가 있다. x = 2.6180에 대한 출력 값 y는 표를 보고 y = 1.5라는 것을 알 수 있다. 만약 저 표에 없는 입력 값 x = 1.7894에 대한 출력 값 y를 알고 싶다면 어떻게 해야 될까? 이러한 궁금증을 풀기 위해 등장한 것이 바로 회귀(Regression)이다. 회귀란 알고 있는 데이터 값들을 이용하여 그 값들을 최대한 가깝게 지나면서 데이터 사이사이에 있는 다른 값들을 예측해내는 함수를 찾는 과정이다. 그때 회귀선이 직선 형태를 하고 있으면 선형 회귀(Linear Regression)라 하고, 직선이 아닌 2차 또는 3차 곡선, 삼각함수 곡선 형태를 하고 있으면 비선형 회귀(Non Linear Regression)이라고 한다.
선형 회귀란 주어진 데이터를 가장 잘 표현하면서 데이터 사이의 오차를 최소화하는 직선이다. 선형 회귀는 1차 함수를 찾을 수 있다는 가정 하에 어떠한 입력 값에 대해서도 출력되는 값을 찾는다(회귀 문제)는 것을 내포하고 있다. 선형 회귀를 구하기 전에 먼저 데이터의 입·출력 값의 개수를 고려하여 좌표평면이나 좌표 공간에 나타내 보아야 한다. 그리고 데이터에 어울리는 함수를 무엇으로 할지 정해야 한다. 선형 회귀의 경우 1차 함수의 합의 꼴로 가설 함수를 설정해야 한다. (이렇게 설정된 가설함수는 실제 데이터들의 점들을 통과하거나 적어도 점들은 가까이 지나간다.)
선형 회귀를 구할 수 있는 기법은 어떤 식으로 접근하느냐에 따라 다양한 방식으로 해결할 수 있다. 통계학의 시각에서 선형 회귀를 간단히 spss통계분석 소프트웨어나 Excel 등을 이용하여 구할 수 있다. 수학에서는 최소제곱법(Least Square Solution), 내리막 경사법(Gradient Descent Method), 뉴턴법(Newton Method) 등으로 접근하여 구할 수 있다. 필자는 그 중에 내리막 경사법(Gradient Descent Method)을 사용하여 주어진 데이터를 가지고 선형 회귀를 구할 것이다.
Step 1. 가설 함수 설정
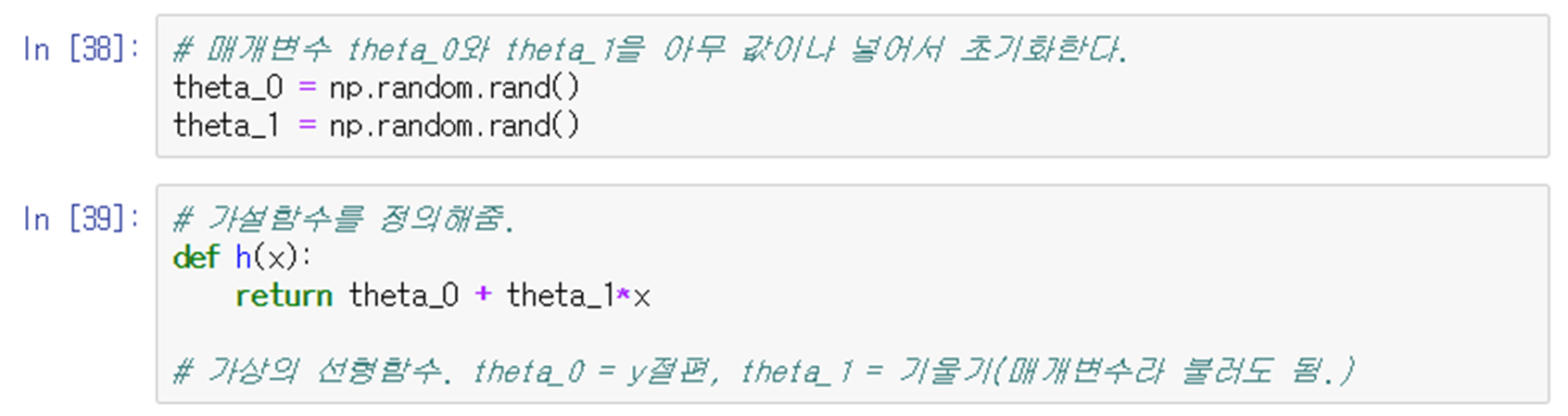
주어진 데이터는 입력 값(x) 한 개, 출력 값(y) 한 개 이므로
라고 정의할 수 있다.
Step 2. 오차식
회귀에서 가장 이상적인 회귀선은 실제 데이터와 예측하고 싶어 하는 값을 구해줄 가설 함수와의 오차가 0인 회귀선을 찾는 것이다. 그러므로
은 오차식을 나타낸다.
Step 3. 손실함수 정하기
손실함수는 오차식에 각각의 데이터에 해당하는 오차의 제곱의 합으로 표현한 함수이다.
이 식은 점과 선의 최단거리를 구하는 데에 중점을 두고 구한 것이다. 그리고 최소제곱법을 이용하여 제곱의 합의 오차를 최소화(오차->0)하여 최솟값을 찾는다.
Step 4. 내리막 경사법을 이용하여 손실함수 미분
< 내리막 경사법(Gradient Descent Method) >
해를 반복 개선하는 수치적 방법의 일종으로 미분계수(평균변화율)(즉, 미분)을 이용하여 도함수의 부호에 따라 자연스럽게 경사가 가장 급격하게 떨어지는 방향을 찾아 x값을 옯기면서 함수의 최솟값을 찾는 방법이다.
내리막 경사법을 식으로 써보면
이다. 여기서, 𝛼는 학습률(learning rate)이다. 이것은 손실 함수 𝐽(𝜃)가 최솟값에 도달하게 하는데 가장 가파른 감소 방향으로 반복적으로 걸리는 매우 자연스러운 알고리즘이다.
이제 미분을 해 줄 거다.
Step 5. 코딩
Step 1.부터 Step 4.까지를 이용하여 코딩을 해준다.
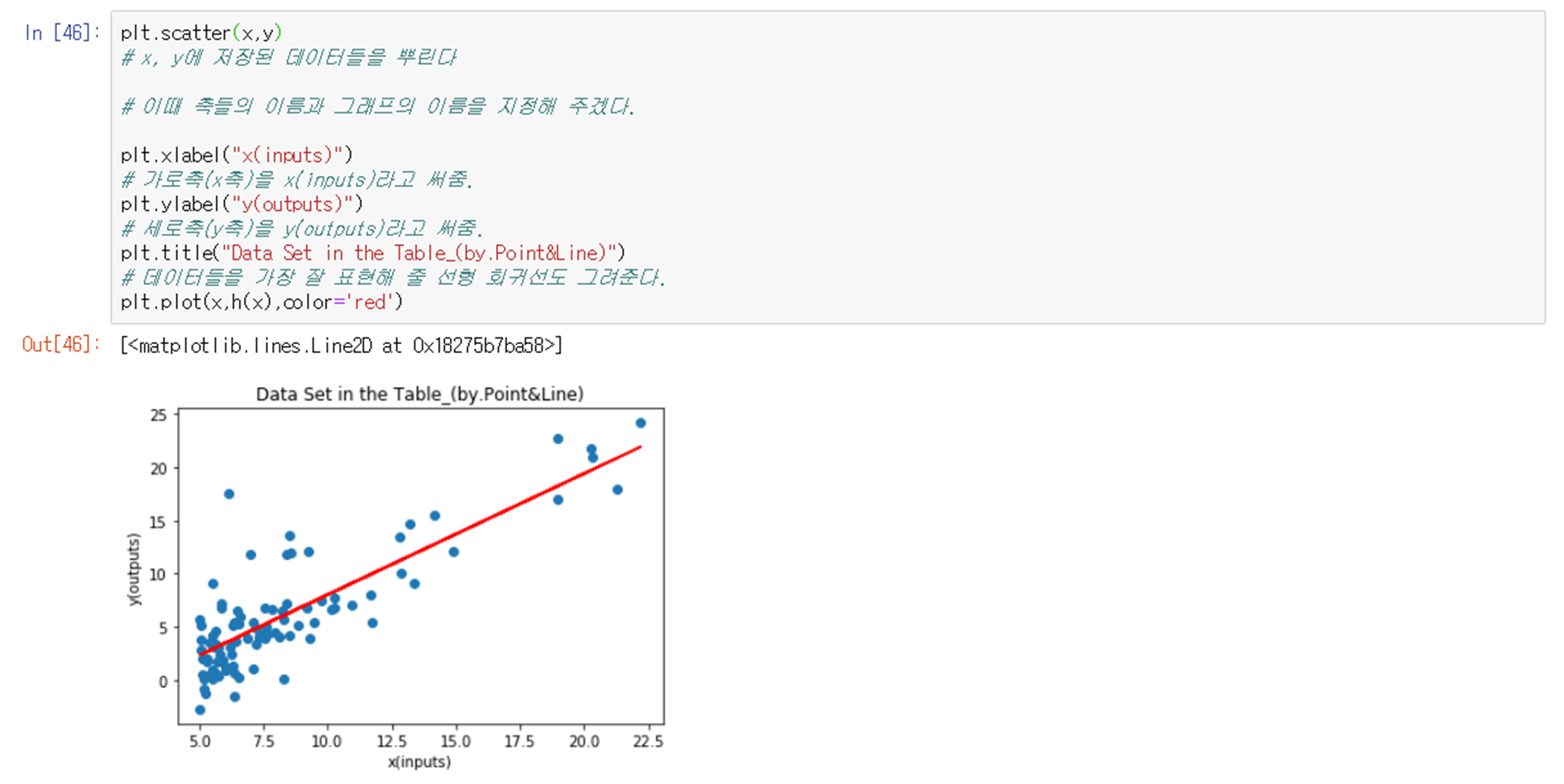
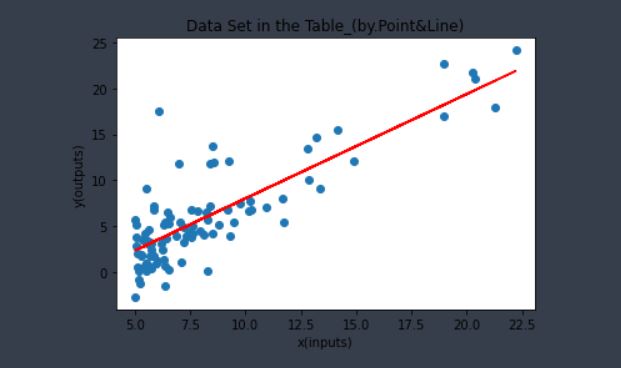
Step 6. 코드 결과 및 분석
내리막 경사법(Gradient Descent Method)를 이용하여 주어진 데이터를 가지고 선형 회귀를 만들어 보았다. 선형 회귀는 원시 데이터를 최적의 직선으로 나타내고 예측 값을 대략적으로 알려주기 때문에 정확한 값을 기대 해서는 안 된다. 다만 선형 회귀를 직접 이해하면서 느낀 거 중 선형 회귀를 이용한다면 최상의 선택은 할 수 있을 것으로 보인다.
Reference (Source Code)
Soli Deo Gloria. / Sapere Aude.