
[딥러닝] 과적합, 오차 역전파, 경사하강법
에 이어 Gradient descent에 대해 조금 더 자세히 다뤄보고자 한다.
1. Gradient descent(GD) 가 뭔데?
주어진 함수의 최소 값을 찾아 나가는 iterative한 1차 Optimization 알고리즘
1.1 Optimization(최적화)?
Optimization refers to the task of either minimizing or maximizing some function f(x) by altering x.
-
parameter(여기선 )값을 변경하여 함수 를 최소화 및 최대화 하는 것을 의미함 -
보통은
minimizing(최소화)측면에서 Optimization을 함!
( 최대화 하고싶으면 그냥 앞에-붙이면 되니까~ ) -
최소화 하고자 하는 함수 (여기선 )를
->objective function(목적함수)
(cost function,loss function,error function라고도 함)
1.2 1차?
- Gradient descent는 1차 도함수 형태를 이용한다.
- 즉, 1번 미분한 값을 이용한다.
- 자세한 내용은 아래에서 수식을 통해 설명할 것임!
1.3 2차 함수에서 최솟값 찾기
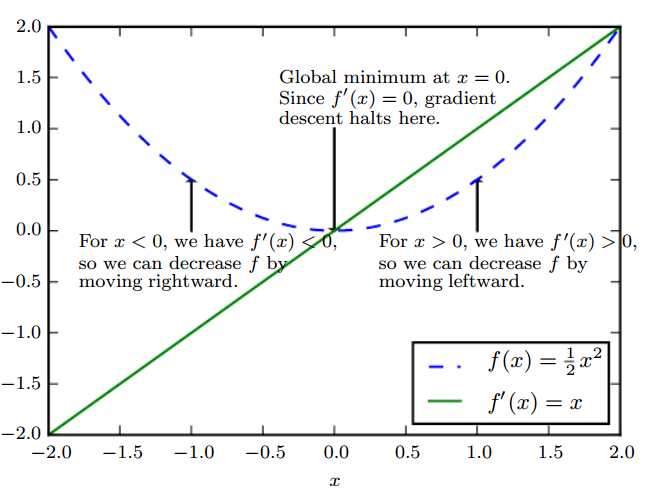
(이미지 출처: Deep Learning Book by Ian GoodFellow)
- 그림에서와 같이 의 최솟값을 찾기 위해
- 임의의 점을 정하고, 그 점이
- 라면, 함수의 기울기 가 음수(-)이므로 현재 값보다 오른쪽 값이 더 작을 것이다. 따라서 더 작은 값을 찾기 위해 오른(+방향)쪽으로 움직인다.
- 라면, 기울기가 양수(+)이므로 같은 개념으로 왼쪽(-)으로 이동한다.
- 즉, 현재 기울기()의 반대 방향으로 움직인다.
기울기(Gradient)의 반대(descent)로 움직인다.
그래서Gradient descent이다.
2. 이렇게 최솟값을 찾으면 뭐가 좋은데?
-
그냥 도함수()를 구해 0이 되는 점을 찾으면 간단하지 않을까 생각할 수 있다.
- 간단하지! 만약 그게 위와 같은 2차 함수라면...
-
그치만 현실세계에선 그렇지 않다.
- 최적화 하고자 하는 parameter가 하나가 아니라 엄청 많을 수도.. (다변수)
- 예쁜 convex 함수가 아니라 복잡한 함수 일수도.. 등등
2.1 Convex 함수는 또 뭐야...
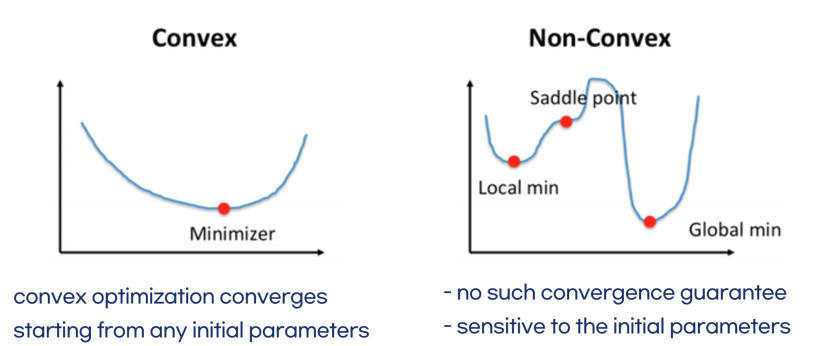
-
아래로 볼록한 함수이다!
-
Covex함수의 경우- 최소값을 찾기 위해 도함수가 0이 되는 점을 찾으면 쉬울 거고
- Gradient descent를 사용하는 경우 아무 점에서나 시작하더라도 최솟값에 도달할 수 있다.
-
그러나 현실 세계는
Non-convex함수에 가깝다.- 미분해서 0이 되는 점을 최솟값이라고 한다 쳐보자.
- 거기서 끝낸다면 오른쪽 그림과 같이 local min일 수 있다.
- 즉, Global min을 못 보고 간과할 수 있다는 소리다.
- 또, saddle point 인 경우 미분해서 0이 되지만, local min도 아니다.
- 이 경우 처음 선택하는 parameter 값에 따라 Global min에 수렴할 수 있는 지 여부가 변할 수 있다.
2.2 Gradient-based Optimize

-
위에서 언급한 현실세계를 반영하기 위해서는
기울기 기반의 최적화 방법을 사용하는 것이 좋다. -
미분계수를 계산하는 과정을 컴퓨터 구현하는 것보다 gradient descent는 더 쉽게 구현 가능함
-
데이터의 양이 매우 많은 경우 gradient descent와 같은 반복적인 방법을 통해 해를 구하면 계산량 측면에서 더 효율적임!
3. 수식으로 알아보자.
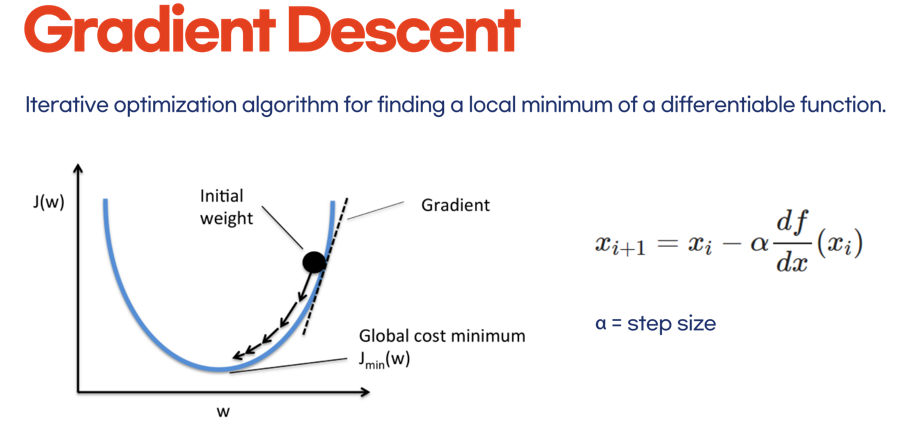
3.1 아 이게 뭔 뜻이냐
현재 값 를 통해 다음 값 를 갱신하고자 할 때,
- 기울기 만큼을 (반대)방향으로 빼 주는 형태
- 그 기울기에 얼만큼의 가중을 둘 건지가,
4. 그래서 이게 딥러닝에서 어떻게 이용되는데?
4.1 최소화 하고자 하는 함수?
-
우리가 최소화 해야할 함수는 딥러닝에서
Loss Function이라고 볼 수 있다. -
Loss 함수는 내가 학습해서 나온 결과와 정답 결과의 차이를 나타내는 함수이다.
4.1.1 Loss 함수의 종류에는
- MSE (Mean Squared Error)
-
RMSE (Root Mean Squared Error)
-
Crossentropy
등이 있다.
4.2 예를 들어보자

-
아래와 같은 손글씨 숫자 사진이 있다고 해보자.
-
사람 눈으로 보면 당연히 5라고 쉽게 판단한다.
-
그런데 컴퓨터에 학습시키기 위해서는 한 pixel씩 뜯어봐야 한다.
-
여기서는 그렇게 중요한게 아니므로, 뭐 이리저리 하나씩 잘 뜯어가지고 학습 시킨다고 하자.
-
그러면 예측한 결과 데이터는 0~9까지의 숫자인 10개의 class로 분류될 것이다.
-
그것을 프로그래밍적으로 나타내고자 한다면,
- 정답 배열 은
0 0 0 0 0 1 0 0 0 0일것이고
(1이 들어있는 5번째 값이 정답이라는 뜻) - 예측한 배열 은
0.2 0.3 0.1 0.2 0.1 0.99 0.1 0.1 0 0
라고 가정해보자.
- 정답 배열 은
-
위의 Loss함수 중 MSE를 사용한다고 했을 때 아래와 같을 것이다.
-
그리고 우리가 최소화 하고자 하는 그 손실 함수는 바로 이 값이다!
-
정답과의 차이를 줄여보자는거지~
4.3 어떻게 차이를 줄이는데?
-
가중치(weight)를 갱신하면서 줄이는 것이다.
-
즉, 위에서 언급한 식을 가중치()에 활용한다.
-
여기서 는 Loss함수를 의미하고,
-
의 값에 따른 Loss함수의 값을 줄이기 위해 최적화 된 를 찾는 것이다.
-
는 딥러닝에서
Learning rate를 의미한다.
즉, 얼마나 이 기울기에 비중을 둘 것인가... -
즉, 이 그래프의 y축은 Loss함수고, x축이 weight라고 생각하면 된다.
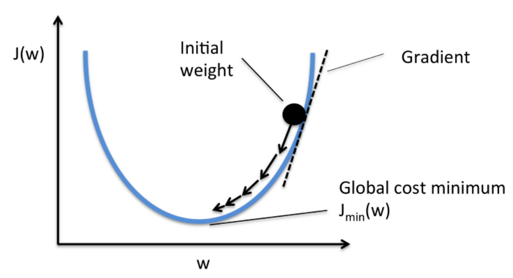
4.4 chain rule (연쇄 법칙)
-
그리고 이 기울기를 구하기 위해 미분의 chain rule이 사용될 수 있다.
-
여기서 자세하게 다루진 않겠다.
5. Gradient Descent에도 종류가 있다고?
이제 Gradient descent에서 어느정도 이해가 갔을 것이다.
training set이 엄청 많을텐데, 어떤 기울기를 이용해 갱신을 할 것인가에 따라 크게 3가지로 나뉜다.
5.1 Batch Gradient Descent
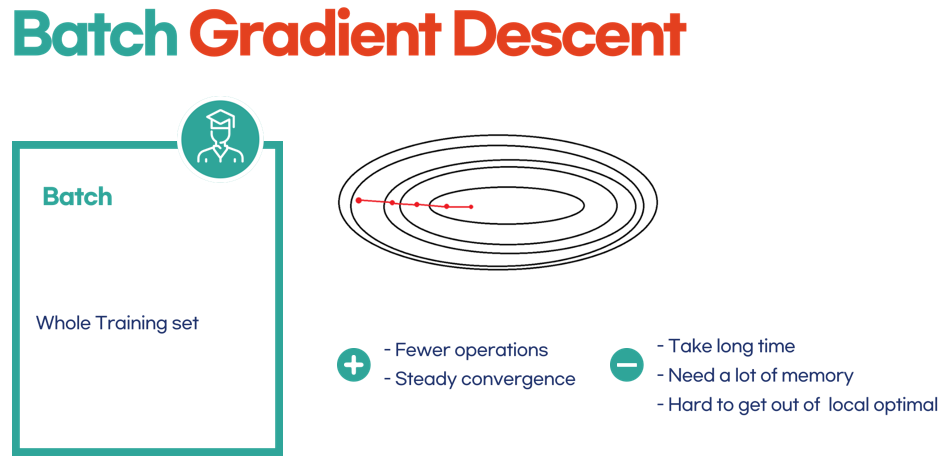
training set 전체를 통해 구하는 방법
- 전체를 반영하니까 당연히 안정적이겠지
- 그치만 데이터가 얼마나 많은데 전체 데이터를 반영해서 하고 앉아있냐....
시간도 오래걸리고, 메모리도 많이 쓴다. - training set이 많은 경우 불가능할 수도 있다.
5.2 Stochastic Gradient Descent
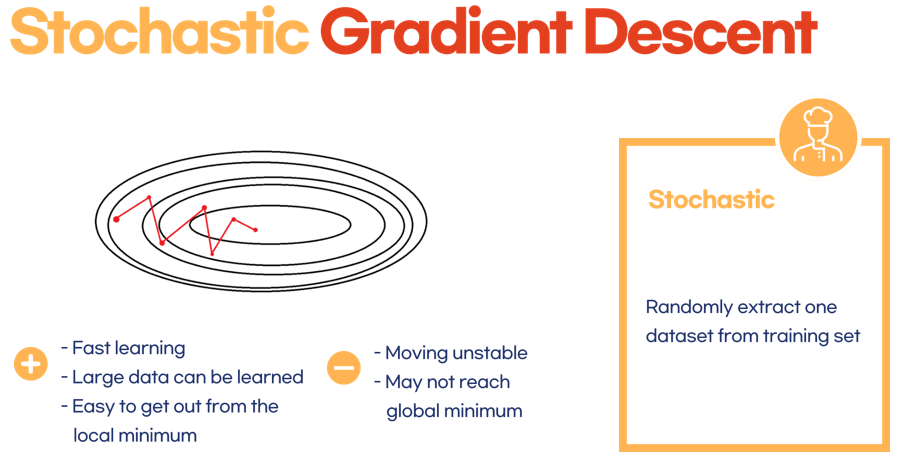
랜덤하게 하나만 뽑아서 구하자!
- 랜덤이든 순차적이든 하나만 뽑아서 그에 대해 기울기를 구한다.
- 일단 하나만 가지고 하니까 당연히 빠르겠지
- 그러니까 당연히 training set이 많은 경우에도 학습시킬 수 있겠지
- 그치만 1개의 데이터는 전체를 반영하기 어렵기 때문에 통통 튈 수 있다.
- 무슨말이냐면 안정적이지 않다는 소리다.
- Global minimum으로 수렴하는 과정에서 위 그림과 같이 지그재그로 막 튄다는 말이다.
- 근데 그렇기 때문에 오히려 local minimum에 빠져버릴 가능성은 또 적다는 이점이 있다.
(batch의 경우 local minimum에 빠져버리면 안정적이기 때문에 쉽게 빠져나오지 못할 수도 있다.)
5.3 Minibatch Gradient Descent
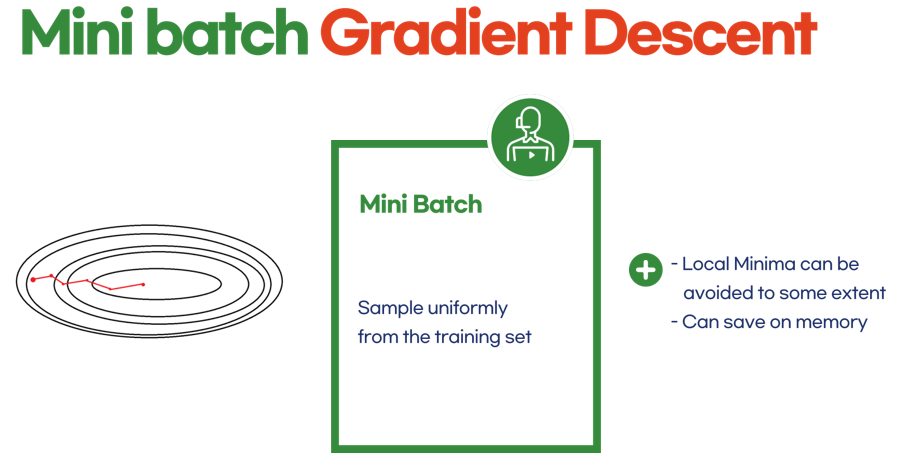
일정한 갯수만 뽑아서 계산하자!
- 하하 위 두가지의 장점만을 병합한 방법이다.
- 예를들어 100개의 샘플만 뽑아서 이에 대한 기울기를 구한다는 의미다.
- 그러면 어느정도 local minima에 빠져버릴 가능성도 줄이고
- 너무 통통 튀는 데이터도 어느정도 완화시킬 수 있을 것이다.
- 그리고 일정 샘플에 대해서만 수행하므로 비교적 큰 training set이 와도 가능하다!
- 실제 학습 시에는 이 미니배치 방법을 많이 활용한다~
아 이정도면 진쨔 자세히 썼다!
