🧐 문제 설명
😍 나의 풀이
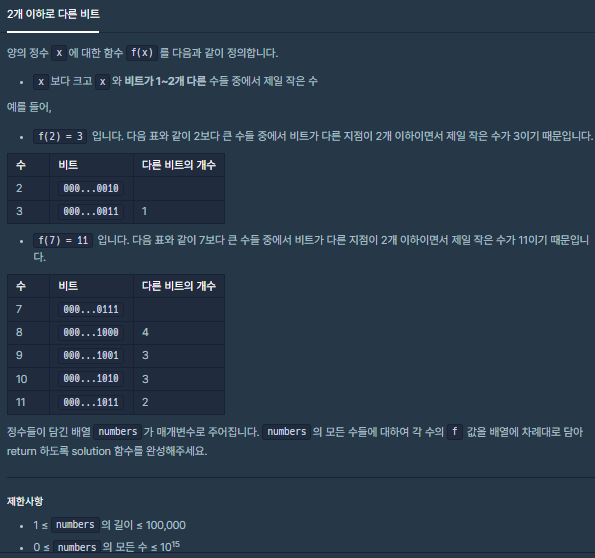
처음 풀이는 아래처럼 서로 다른 비트를 보고 XOR 연산의 특징(비트 연산을 하여 서로 다르면 1, 같으면 0)이 떠올라서 XOR을 쓰면 바로 풀 수 있겠다 싶었다. 하지만 샘플 테스트 케이스는 통과했지만 TC 10, 11에서 시간 초과로 실패했다...
def f(x):
y = x+1
while True:
if bin(x^y).count('1') <= 2:
break
else:
y += 1
return y
def solution(numbers):
answer = [f(i) for i in numbers]
return answer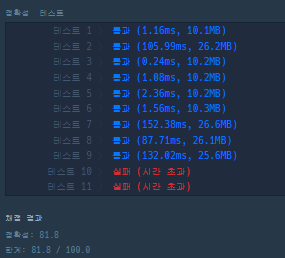
ㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠㅠ
실패 후 다시 내 코드의 문제점을 생각해보니까 양의 정수 x의 값이 최대 10의 15제곱이나 되는 큰 수인데 이걸 2진수로 바꾸고, 또 xor 연산해서 count('1') 한다면 시간이 오래 걸릴 게 당연했다.
또, 1씩 증가시키면서 이 과정을 반복하기 때문에 만약에 비트 자리 수가 너무 클 경우 조건을 만족하는 f(x)의 값을 구하는 데 시간이 오래 걸릴 수 밖에 없었다.
보통 이런 범위가 커서 시간 초과를 유도하는 문제는 일반적인 로직보다 문제를 훨씬 간단하게 만드는 규칙을 찾는 것이 해법이 될 때가 많다.
이 문제도 짝수일 때는 제일 끝에 비트가 무조건 0이기 때문에 +1한 값이 비트가 1개 차이나면서 가장 작은 숫자가 된다. 홀수일 때는 조금 다른데 끝에서부터 0을 찾아서 0을 1로 바꿔주면 비트 차이가 2개 이하인 숫자가 된다. 하지만, 이 값이 가장 작은 수라고 할수는 없다. 가장 작은 수가 되려면 0을 1로 바꾼 비트 자리 다음 비트를 0으로 만들어야 가장 작은 수가 된다.
def f(x):
if x % 2 == 0: #짝수면 비트 끝 자리가 무조건 0이기 때문에 한 비트 차이나는 가장 작은 값은 +1한 값
return x+1
else:
y = '0' + bin(x)[2:]
idx = y.rfind('0')
y = list(y)
y[idx] = '1'
y[idx+1] = '0'
return int(''.join(y), 2)
def solution(numbers):
answer = [f(i) for i in numbers]
return answer'0'을 초기에 넣어주는 이유는 예를 들어, 7의 경우 111이기 때문에 0을 찾을 수가 없는 문제가 생기므로 0111로 만들어서 조건에 만족하는 1011을 유도해내기 위해서 처음에 '0'을 넣어준다. 이후 이진수로 변환한 문자열에서 rfind()를 통해서 우측부터(끝 자릿수 비트) '0'의 인덱스를 찾아서 그 값을 1로 바꾸고 그다음 인덱스는 0으로 바꾼다.
이 과정에서 처음엔 문자열 인덱스로 접근했는데 문자열 인덱스는 값은 출력할 수 있어도 y[idx] = '1' 이렇게 문자열 일부를 변경하는 것은 불가능했다. 만약 문자열을 리스트로 바꾸지 않고 처리하려했다면 y[:idx] + '1' + y[idx+1:] 이런식으로 슬라이싱을 이용해야 한다. 나는 리스트를 이용해서 처리하고 이후 join을 이용해 다시 문자열로 출력했다.
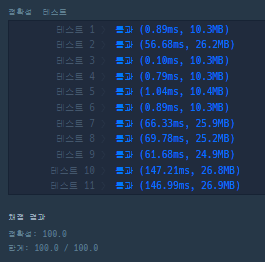
👏다른 사람의 풀이

def solution(numbers):
answer = []
def cal(n):
last = (~n) & (n+1) #최하위비트 0이 있는 위치
return (n|last) & ~(last>>1)
for n in numbers:
if n%2 == 0 :
answer.append(n+1)
else: #홀수인경우
tmp = cal(n)
answer.append(tmp)
return answer🥇 Today I Learn
비트 마스크(Bit Mask) 활용
공집합과 꽉찬 집합 구하기
= 토핑이 아예 없는 피자와, 토핑이 꽉 찬 피자 구하기.
-
토핑이 없는 피자
emptyPizza = 0 -
토핑이 꽉찬 피자
fullPizza = (1<< 10) - 1
원소 추가
= 피자 a 에 n 번 토핑 추가하기 (단, 0 <= n < 10)
현재 피자에 특정 값만 0 에서 1 로 바꾸고 싶은 경우이다.
이미 해당 토핑이 들어가 있다면 그냥 1로 유지하면 된다.
a = a | (1 << n)
즉, 축약하면
a |= (1 << n)
최하위 비트 찾아내기
leastSignificantTopping = a & -a
ex) 예를들어 5자리 숫자 40 이라고 해보자
-40은 2의 보수 연산법 을 사용하여 아래와 같이 (01100) 이 된다.
10100 = 40
01011 + 1 = 01100 = (-40)
10100 & 01100 = 00100 (2^3)최소 비트 지우기
= 피자 a 에 올라간 토핑들 중 가장 작은 자릿수의 토핑 빼기
removedToppings = a & (a - 1)
ex) 10110 = a 일때,
10110 & (10101) = 10100
이것말고도 많은데 이 문제에서 쓰인 것만 정리했다. Bit Mask에 대해서 따로 정리를 하고 문제를 풀어봐야겠다

