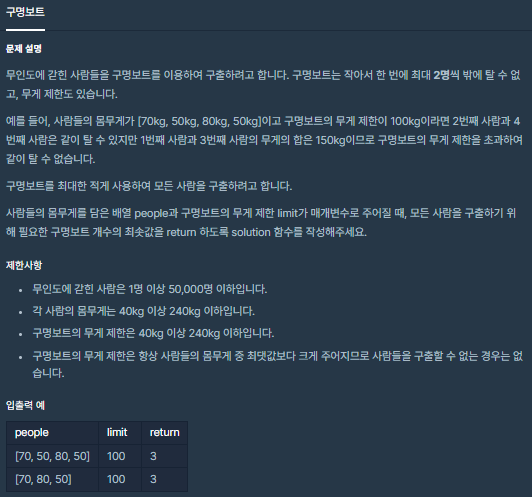
🧐 문제 설명
😍 나의 풀이
Greedy 알고리즘을 어떻게 사용할 것인가가 핵심인 문제. 보트를 가장 적은 횟수로 사람들을 이동시키려면 제일 무거운 사람, 제일 가벼운 사람을 같이 묶어서 처리해야한다는 게 핵심 아이디어다.
-
people 리스트를 덱으로 만든 후 내림차순 정렬
-
무거운 사람(왼쪽)과 가벼운 사람(오른쪽)을 인덱스로 매칭
-
합이 보트 무게보다 가벼우면 둘 빼냄
-
보트 무게보다 무거우면 무거운 사람만 빼냄
from collections import deque
def solution(people, limit):
answer = 0
people = deque(sorted(people, reverse = True))
while len(people) > 1:
if people[0] + people[-1] <= limit: # 최댓값과 최솟값 묶어서 보트태움
answer += 1
people.pop() #최소 빼내고
people.popleft() #최대 빼내고
else:
answer += 1
people.popleft()
if people: #people에 1명 남아있는 경우 처리
answer += 1
return answer👏 다른 사람의 풀이
def solution(people, limit) :
answer = 0
people.sort()
a = 0
b = len(people) - 1
while a < b :
if people[b] + people[a] <= limit :
a += 1
answer += 1
b -= 1
return len(people) - answer- 배울만한 코딩 SKILL
-
인덱스를 start, end 시점으로 투 포인터로 접근
-
while문의 조건을 보면 인덱스 같아지는 시점(people의 모든 요소 다 조사됨)을 a<b로 표현한 것도
자주 보는데 난 잘 못 씀ㅠㅠ -
또 return 값이 결국 len(people) - answer인 것은 전체 한 번은 옮겨야 하는데 가장 가벼운 것과 가장 무거운 것이 묶어서 되는 경우는 2명이 한 보트로 처리되기 때문에 전체에서 그 경우를 빼주려고 한 것 같다.
🥇 Today I Learn
Greedy (탐욕법, 탐욕 알고리즘)
Greedy Algorithm은 문제를 해결하는 과정에서 그 순간순간마다 최적이라고 생각되는 결정을 하는 방식으로 진행하여 최종 해답에 도달하는 문제 해결 방식이다.

위의 그림에서는 가장 숫자가 큰 요소를 찾는데 있어서 해당 분기점마다 보다 큰 수를 찾는 방식으로 최종 해답을 찾아가고 있다. 순간마다 큰 수를 찾아가면 최종 결과는 12이다. 하지만 실제 전체 숫자 중에서 가장 큰 수는 99이다. 이처럼 전체 문제해결에서의 최적 해답을 찾지는 못한다.
하지만 이러한 단점들을 극복하는 Greedy의 가장 큰 장점은 계산 속도에 있다. 그래서 Greedy 방법이 통하는 몇몇의 문제에서는 최적해를 빠르게 산출해낼 수 있다.
투 포인터 (Two Pointer)
-
배열 안에 있는 값들을 연속해서 더하거나 연산하는 경우에 사용 인덱스를 가리키는 두 개의 변수(포인터)를 선언하여 사용하는 특징이 있어 투 포인터라 불림
-
예를 들어 N개의 숫자가 들어있는 배열이 주어질 때, 부분 집합의 합이 특정 숫자인 M인 경우의 수를 구하는 문제에 적용한다면, 배열의 인덱스를 가리키는 startPointer와 endPointer를 생성한 후 특정 규칙에 의해 각 포인터를 움직여 배열을 탐색해 문제를 해결할 수 있으며, 그 규칙은 다음과 같습니다.
1-1) 현재까지의 합이 M보다 크거나 같은 경우 합에서 endPoiner가 가리키고 있는 값을 뺀 후 endPointer를 +1 증가시킵니다.
1-2) 만약 startPointer의 값이 배열의 길이와 같을 경우 탐색을 종료합니다.
1-3) 나머지 경우(현재까지의 합이 M보다 작을 경우)에는 합에 startPointer가 가리키고 있는 값을 더한 후 startPointer를 +1 증가시킵니다.
2) 위의 세 규칙 중 해당하는 연산이 끝난 후 만약 현재까지의 합이 M과 같다면 답을 +1증가 시킵니다.
-
투 포인터를 사용한다면 한 번 답이 될 수 없다고 판명된 이후의 값들을 더 이상 탐색하지 않으므로 시간 복잡도가 O(n)이 되어 완전 탐색에 비해 효율이 훨씬 좋음

