[프로그래머스] LEVEL2 (완전 탐색) 소수 찾기 (Python)

[프로그래머스] LEVEL2 (완전 탐색) 소수 찾기

---

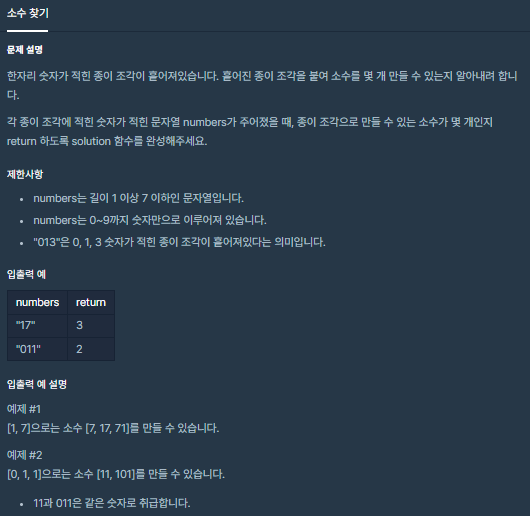
🧐 문제 설명

---

😍 나의 풀이

전에 [프로그래머스] LEVEL2 후보키 문제를 풀 때 combinations를 사용한 것이 생각나는 문제였다. 그런데 여기서는 "17"이 주어졌을 때, 예를 들어 2인자로 조합해서 나오는 (1, 7) = 17 뿐 아니라 (7, 1) = 71에 대해서도 고려해야한다. 즉, 순서가 상관이 있기 때문에 조합이 아닌 순열로 풀이해야 한다.

1. permutations 의 모든 경우의 수를 리스트에 extend
2. 각각 값을 정수로 변환해서 저장(이 과정에서 앞자리에 0이 있는 '011'은 11으로 정리됨)
3. set으로 중복 제거 후 소수 판별

from itertools import permutations

def sosu(n):
    if n < 2:
        return False
    
    for i in range(2, n//2+1):
        if n%i == 0:
            return False
        
    return True    

def solution(numbers):
    answer = 0
    p = []
    result = []
    
    for i in range(1, len(numbers)+1):
        p.extend(permutations(numbers, i))
        result = [int(''.join(i)) for i in p]
    
    for i in set(result):
        if sosu(i):
            answer+=1
            
    return answer

---

👏 다른 사람의 풀이

set의 중복이 불가능하고 뺄셈이 가능한 특징과 소수 판별에서 에라토스테네스의 체를 이용한 풀이가 인상적이었다.

from itertools import permutations
def solution(n):
    a = set()
    for i in range(len(n)):
        a |= set(map(int, map("".join, permutations(list(n), i + 1))))
    a -= set(range(0, 2))
    for i in range(2, int(max(a) ** 0.5) + 1):
        a -= set(range(i * 2, max(a) + 1, i))
    return len(a)

---

🥇 Today I Learn

한 가지 착각하고 있던 게 있었는데 Set 자료구조는 Noniterable하므로 반복문에 들어가지 못한다고 잘 못 알고 있었는데 그냥 Indexing이 안되는 거지, for문은 돌 수 있음!!!

에라토스테네스의 체

• 범위의 모든 소수를 구할 때 효율적

1. 1은 제거

2. 지워지지 않은 수 중 제일 작은 2를 소수로 채택하고, 나머지 2의 배수를 모두 지운다.

3. 지워지지 않은 수 중 제일 작은 3을 소수로 채택하고, 나머지 3의 배수를 모두 지운다.

4. 지워지지 않은 수 중 제일 작은 5를 소수로 채택하고, 나머지 5의 배수를 모두 지운다.

5. (반복)

n=1000
a = [False,False] + [True]*(n-1)
primes=[]

for i in range(2,n+1):
  if a[i]:
    primes.append(i)
    for j in range(2*i, n+1, i):
        a[j] = False
print(primes)