[BOJ/python] 2193: 이친수

문제

✔️ silver 3
다이나믹 프로그래밍

문제 흐름

천천히 패턴을 적어보면 금방 알 수 있는 문제였다.

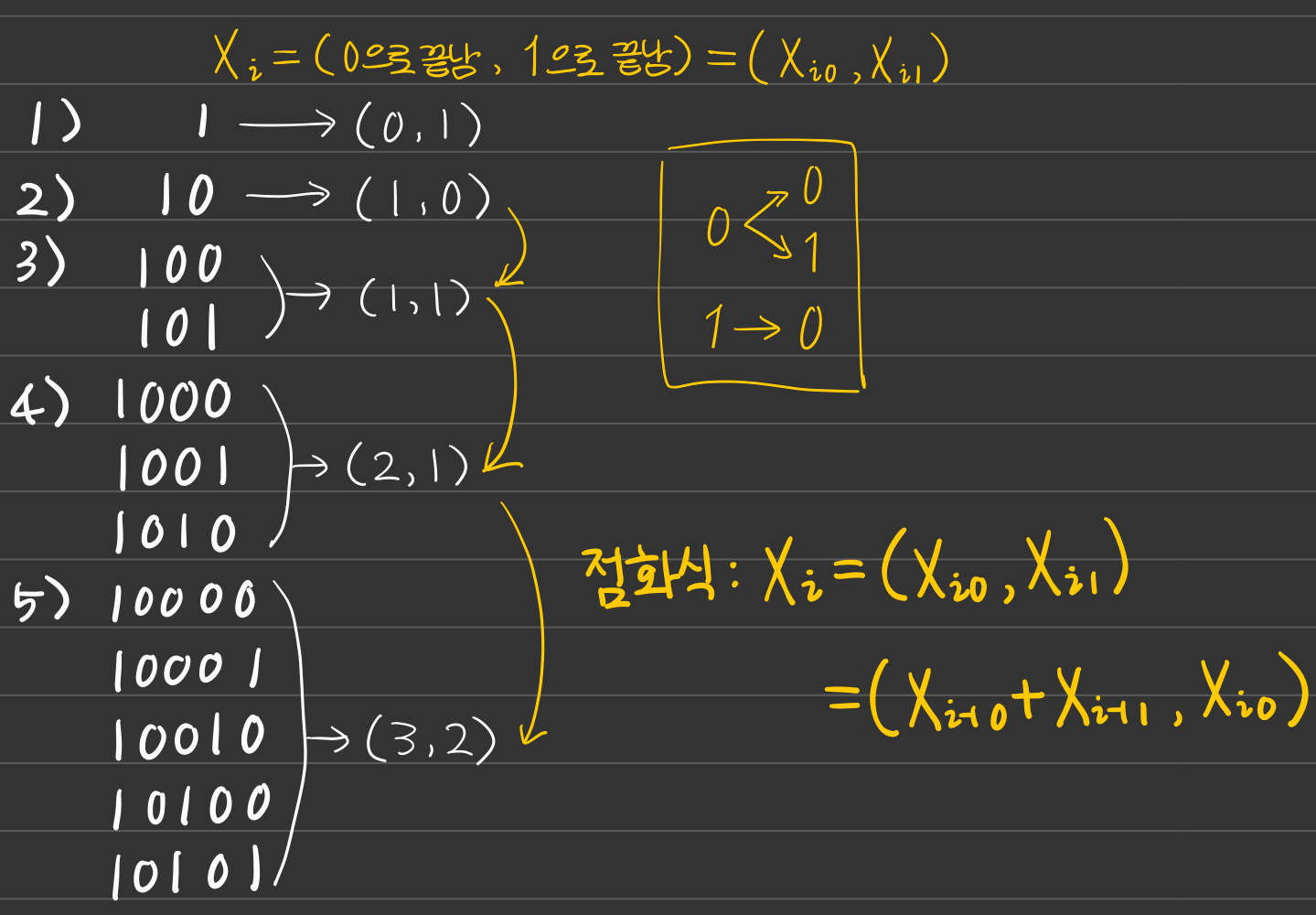맨 앞자리는 1, 두번째 자리는 0으로 정해져있고, 그 뒤에 오는 수가 0인지 1인지에 따라 경우의 수가 갈린다. 0인 경우 0 또는 1이 올 수 있다. 1인 경우 0만 올 수 있다.

이전 단계의 0으로 끝나는 수만큼 0과 1으로 끝나는 수가 생겼을 거고, 1으로 끝나는 수만큼 0으로 끝나는 수가 생겼을 것이다.
따라서 0으로 끝나는 수와 1로 끝나는 수를 각각 i마다 계산해서 저장해두면 쉽게 다음 단계의 경우의 수들을 구할 수 있다.

코드

# 이친수
# dp

import sys
input = sys.stdin.readline

def dp (n: int):
    if n == 1 or n == 2:
        return 1
    
    memo = [(0,0) for i in range(n + 1)]
    memo[1] = (0, 1)
    memo[2] = (1, 0)
    for i in range(3, n + 1):
        memo[i] = (memo[i - 1][0] + memo[i -  1][1], memo[i - 1][0])
    
    # print(memo)
    res = sum(memo[n])
    return res


if __name__ == "__main__":
    n = int(input())
    result = dp(n)
    print(result)

마무리

여러 차례 DP문제를 풀어보며 느낀 점이 있다.
고정된 점이 있다면 거기서부터 시작하는 게 좋고,
최댓값이나 최솟값 등 조건에 맞춰 계산해야된다면 보통 거꾸로 계산하는게 잘 들어맞는 것 같다..!

그리고 손으로 쓰기 시작하면서 알게 됐는데, 습관적으로 확률변수처럼 DP 순열(?)을 나타내고있는 것 같다. 안쓴지 정말 오래됐는데,,, 그래도 익숙한가보군. 신기하다.