[BOJ/python] 2240: 자두나무

문제

✔️ gold 5

문제 흐름

memo[i][j]를 i번째 자두가 떨어질 때 j번 이동한 경우 받은 최대 자두 수로 설정하고 규칙을 찾았다.
각 memo[i][j]는 memo[i-1][j-1], memo[i-1][j] 를 통해서 구할 수 있다.
처음 자두가 위치한 나무는 1번 나무이기 때문에 자두가 홀수번 이동하면 2번 나무에 위치하고, 짝수번 이동하면 1번 나무에 위치함을 알 수 있다.

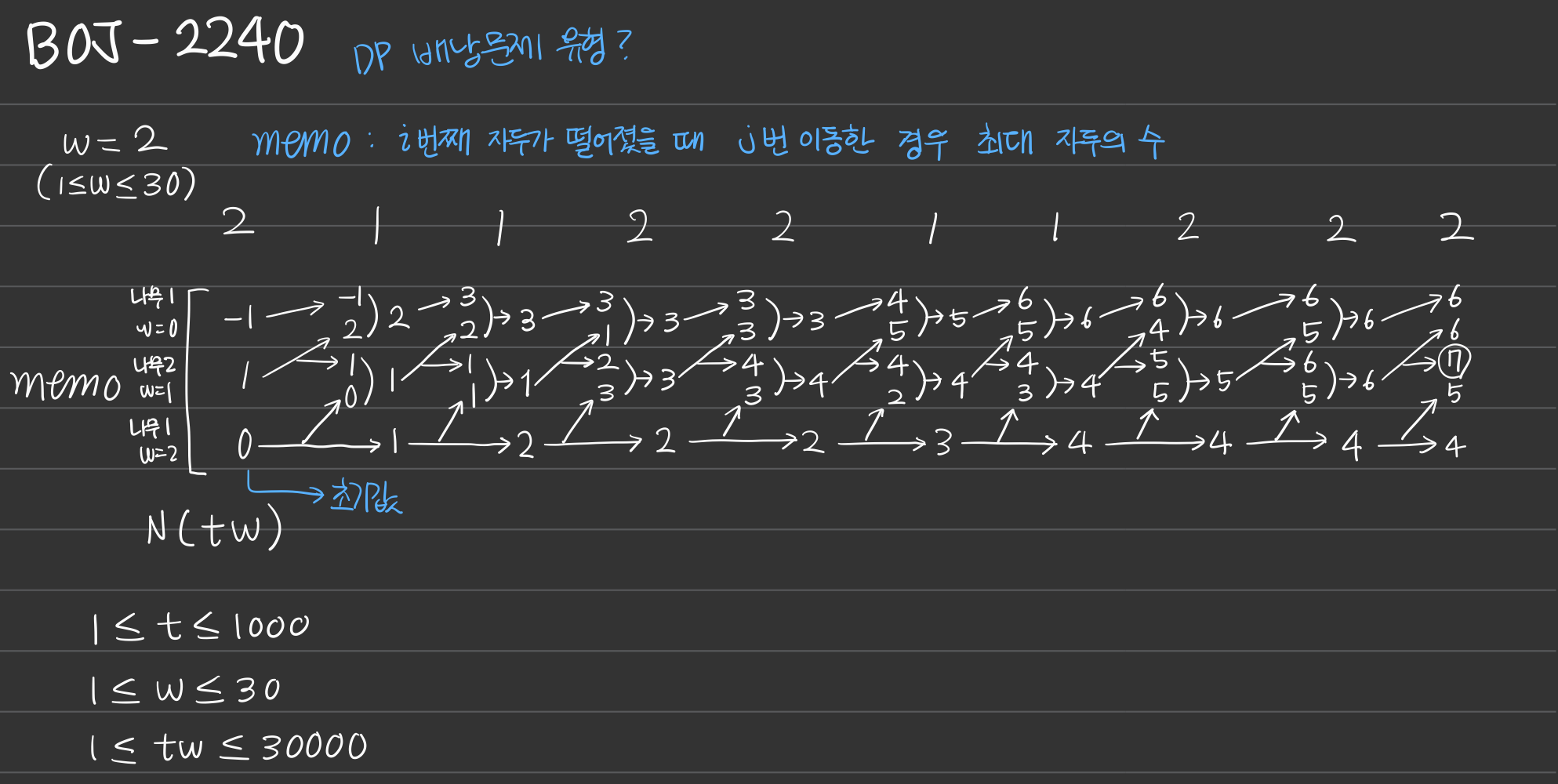
위 그림과 같은 방식으로 계산을 진행했다.
각 행은 아래서부터 위 순서로 0번 ~ w번 이동함을 나타낸다.
열은 자두가 떨어진 나무를 나타낸다.
각 경우에 대해서 두 케이스가 있고, 그중 큰 값을 가지도록 한다.

이를 코드로 구현할 때, memo는 0과 구분하기 위해 모두 -1의 값을 가지도록 초기화했다.
초기값은 가장 처음 떨어진 자두에 대한 값으로, 첫 자두가 어느 나무에 떨어졌는지에 따라 0번, 1번 이동한 경우를 수정해주면 된다.

점화식을 코드로 간단히 써보자면 이렇다.

# 초기값
if plum[0] == 1:
	memo[0][0] = 1
    memo[0][1] = 0
else:
	memo[0][0] = 0
    memo[0][1] = 1
    
# 자두가 떨어진 나무에 위치한 경우
memo[i][j] = max( memo[i-1][j-1] + 1, memo[i-1][j] + 1)
# 자두가 떨어지지 않은 나무에 위치한 경우
memo[i][j] = max( memo[i-1][j-1], memo[i-1][j])

단, j == 0인 경우 그림의 가장 아래 행에 해당하게 되는데,
j-1 인덱스에서 가져올 수 없으므로 이에 대한 처리를 따로 해줘야 한다.

코드

# 자두나무
# DP

import sys
input = sys.stdin.readline

def dp (plum: list, w: int):
    t = len(plum)
    # memo[i][j]: i번째 자두가 떨어질 때 이동을 j번 한 경우 받은 최대 자두 수
    memo = [[-1 for i in range(w + 1)] for i in range(t)]
    
    if plum[0] == 1:
        m_0 = [1, 0]
    else:
        m_0 = [0, 1]
    m_0.extend([-1 for i in range(w - 1)])
    memo[0] = m_0

    for i in range(1, t):
        for j in range(0, w + 1):
            # print(f"Calculating memo[{i}][{j}]")
            if j == 0:
                if plum[i] == 1:
                    memo[i][j] = memo[i - 1][j] + 1
                else:
                    memo[i][j] = memo[i - 1][j]
                # print(f"  No move: memo[{i}][{j}] = {memo[i][j]}")
                continue
            # j(이동한 횟수)가 짝수면 1번 나무에 있는 것
            if j % 2 + 1 == plum[i]:
                val_1 = memo[i - 1][j - 1] + 1
                val_2 = memo[i - 1][j] + 1
            else:
                val_1 = memo[i - 1][j - 1]
                val_2 = memo[i - 1][j]
            memo[i][j] = max(val_1, val_2)
            # print(f"  memo[{i}][{j}] = max({val_1}, {val_2}) = {memo[i][j]}")
    # print(*memo)
    return max(memo[-1])


if __name__ == "__main__":
    t, w = map(int, input().split())

    plum = []
    for drop in range(t):
        num = int(input())
        plum.append(num)
    
    result = dp(plum, w)
    print(result)