[Python] LCA와 Binary Lifting

🎱 LCA

LCA(Lowest Common Ancestor)는 트리에서 두 노드의 가장 가까운 공통 조상을 찾는 것이다.

• 최소 공통 조상
• 트리 구조 기반

가장 널리 쓰이는 LCA 알고리즘은 Binary Lifting이다.

Binary Lifting에 대해서 알아보자!

🎱 Binary Lifting

Binary Lifting은 모든 노드의 2^k번째 조상을 전처리해둔 뒤, 2^k만큼 위로 점프하며 조상을 빠르게 탐색하는 알고리즘이다.

⚽️ 핵심 개념

1. 각 노드의 깊이와 2^k번째 조상을 저장한다. (전처리)
   • 이때 전처리에 DFS를 이용한다.
2. 2^k씩 위로 점프하며 찾고자하는 조상이 나올 때까지 탐색한다.

⚽️ 자세한 흐름

기준 노드 x를 17로 잡을 경우, x의 3번째 조상을 찾는 자세한 흐름에 대해 살펴보자.
트리는 리스트로, 각 노드 번호의 인덱스에 자식노드를 리스트로 저장해놓은 구조라고 가정한다.

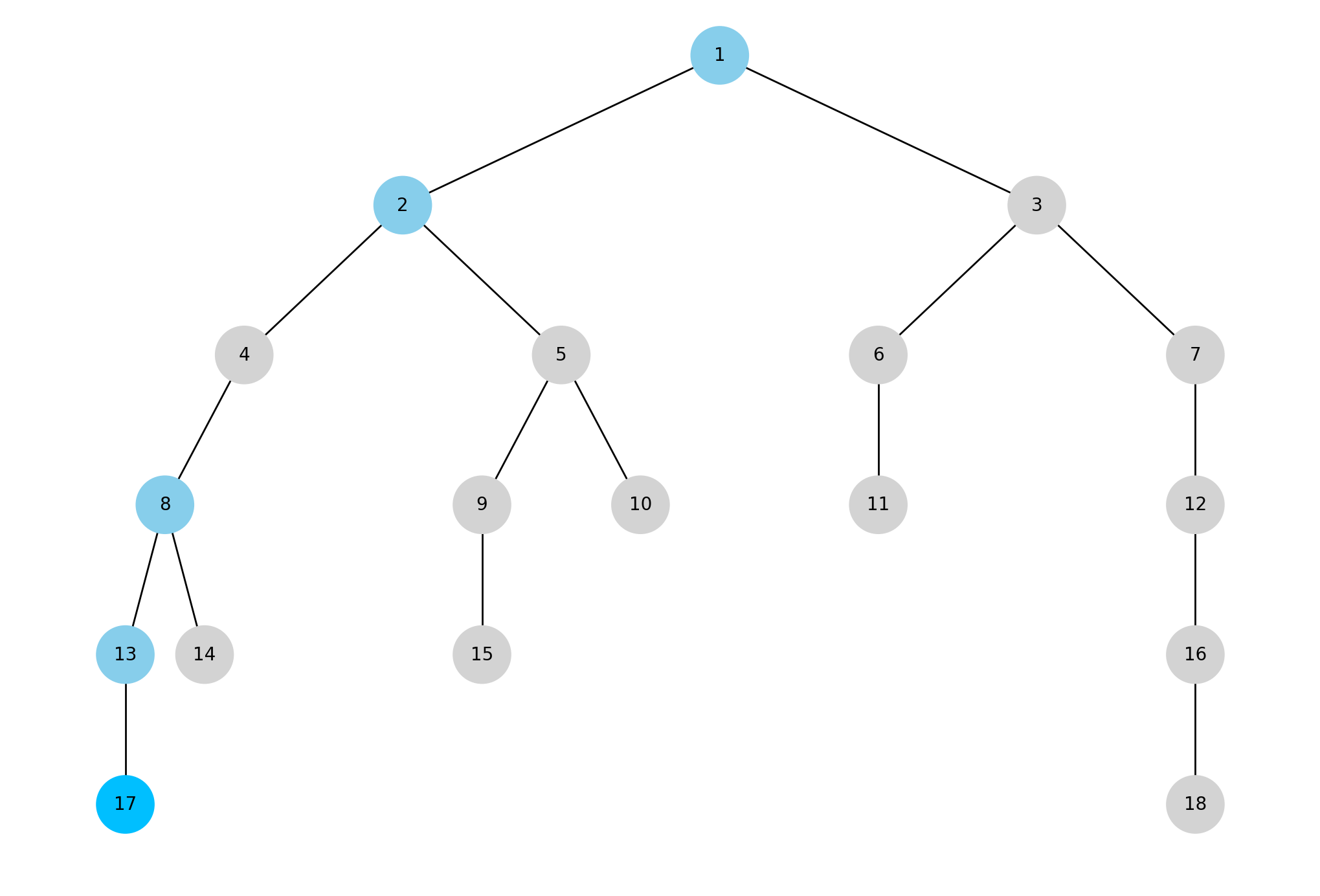
17의 2^k번째 조상을 모두 저장한다.
위 그래프에서는 2^0 = 1, 2^1 = 2, 2^2 = 4, 2^3 = 8 까지가 되겠다.

이 때 DFS를 이용해서 루트에서부터 내려오며 각 노드의 깊이 depth 와 바로 위 부모 parent[x][0] 을 저장한다.

DFS를 다 수행하면 Binary Lifting을 통해 각 노드의 2^k번째 조상을 parent[x] 에 저장한다.
여기서 재귀적인 인덱싱을 사용하는데, 이 이해가 조금 어려울 수 있다.
parent[x][k] = parent[ parent[x][k-1] ] [k-1] 부분인데,
엄마의 엄마, 할머니의 할머니 같은 느낌으로 생각하면 이해가 그나마 잘 된다.
증조 할머니의 증조할머니..

아래 코드는 LCA의 전처리 과정인데, binary lifting이 사용된 것을 확인할 수 있다.
여기서는 완전히 올라가는 흐름이라 이해가 잘 된다.

log = 20

def dfs(tree):
    n = len(tree)
    parent = [[-1 for i in range(log)] for j in range(n)]
    depth = [0 for _ in range(n)]
    
    # dfs
    st = [(1, 0)]
    visited = [0 for _ in range(n)]
    visited[1] = 1
    while st:
        x, d = st.pop()
        for nx in tree[x]:
            if visited[nx]:
                continue
            st.append((nx, d + 1))
            parent[nx][0] = x
            depth[nx] = d + 1
            visited[nx] = 1
    
    # binary lifting
    for k in range(1, log):
        for x in range(1, n):
            if parent[x][k-1] == -1:
                parent[x][k] = -1
            else:
                parent[x][k] = parent[parent[x][k-1]][k-1]
    return parent, depth

⚽️ 언제 사용할까?

• 트리에서 노드 x의 k번째 조상 찾기
• LCA
• 특정 조건을 만족하는 조상 찾기

Binary Lifting은 LCA에서만 쓰이는 알고리즘은 아니다.
그저 조상을 빠르게 탐색하는 알고리즘일 뿐이다.
LCA는 Binary Lifting을 사용할 수 있는 상황 중 하나이다.

그럼 Binary Lifting을 이용한 LCA에 대해서 알아보자.

🎱 Binary Lifting을 이용한 LCA

Binary Lifting을 이용한 LCA는 크게 세가지 단계로 구성된다.

1. 전처리
2. 깊이 맞추기
3. LCA 탐색

전처리에서는 앞서 말했듯, depth 와 parent 를 구한다.
parent를 이용해야 binary lifting이 가능하다.

두 노드 x, y의 LCA를 구하고자할 때 x, y의 깊이가 다르다면 동시에 올라가며 확인할 때 엇갈릴 수 있다.
따라서 두 노드의 높이(깊이)를 맞춰주는 과정이 필요하다.
이때문에 전처리에서 depth 를 구해야한다.

준비를 마쳤다면 마지막으로 LCA를 탐색한다.
여기서의 핵심은 “2^k씩 뛰었을 때, 부모가 같기 직전까지 올라간다”는 점이다.

전체 코드를 통해 확인해보자.

⚽️ 코드 구현

# LCA

import sys
input = sys.stdin.readline

log = 20

def dfs(tree):
    n = len(tree)
    parent = [[-1 for i in range(log)] for j in range(n)]
    depth = [0 for _ in range(n)]
    
    # dfs
    st = [(1, 0)]
    visited = [0 for _ in range(n)]
    visited[1] = 1
    while st:
        x, d = st.pop()
        for nx in tree[x]:
            if visited[nx]:
                continue
            st.append((nx, d + 1))
            parent[nx][0] = x
            depth[nx] = d + 1
            visited[nx] = 1
    
    # binary lifting
    for k in range(1, log):
        for x in range(1, n):
            if parent[x][k-1] == -1:
                parent[x][k] = -1
            else:
                parent[x][k] = parent[parent[x][k-1]][k-1]
    return parent, depth

def lca(x, y, parent, depth):
    # 깊이 맞추기
    if depth[x] < depth[y]:
        x, y = y, x
    for k in reversed(range(log)):
        # 1 << k 는 비트이동을 통한 2**k 표현 (더 빠르다)
        if depth[x] - (1 << k) >= depth[y]:
            x = parent[x][k]
    
    # LCA 구하기
    if x == y:
        return x
    for k in reversed(range(log)):
        if parent[x][k] != parent[y][k]:
            x = parent[x][k]
            y = parent[y][k]
    return parent[x][0]

if __name__ == "__main__":
    n = int(input())
    tree = [[] for _ in range(n+1)]
    for _ in range(n-1):
        x, y = map(int, input().split())
        tree[x].append(y)
        tree[y].append(x)
    
    # 전처리
    parent, depth = dfs(tree)
    
    m = int(input())
    for _ in range(m):
        x, y = map(int, input().split())
        answer = lca(x, y, parent, depth)
        print(answer)

코드는 백준-11437-LCA 문제의 해답 코드다.
해당 문제를 풀며 코드 구현을 통해 직관적으로 이해하고 자세히 공부할 수 있었다.