[Python] MST와 Kruskal, Prim

🎱 MST

MST(Minimum Spanning Tree)는 가중치가 있는 무방향 그래프에서 최소 비용으로 모든 노드를 연결하는 트리를 말한다. “트리”라고 하는 이유는 이 그래프에 cycle이 없어야하기 때문이다.

• 모든 정점 연결
• 사이클 없음
• 가중치의 합이 최소

MST를 찾는 알고리즘은 대표적으로 두가지가 있다.
바로 크루스칼(Kruskal) 알고리즘과 프림(Prim) 알고리즘이다.

둘의 흐름과 핵심 개념, 그리고 구현까지 알아보자!

🎱 Kruskal

크루스칼 알고리즘은 간선을 중심으로 하는 MST 알고리즘이다.

⚽️ 핵심 개념

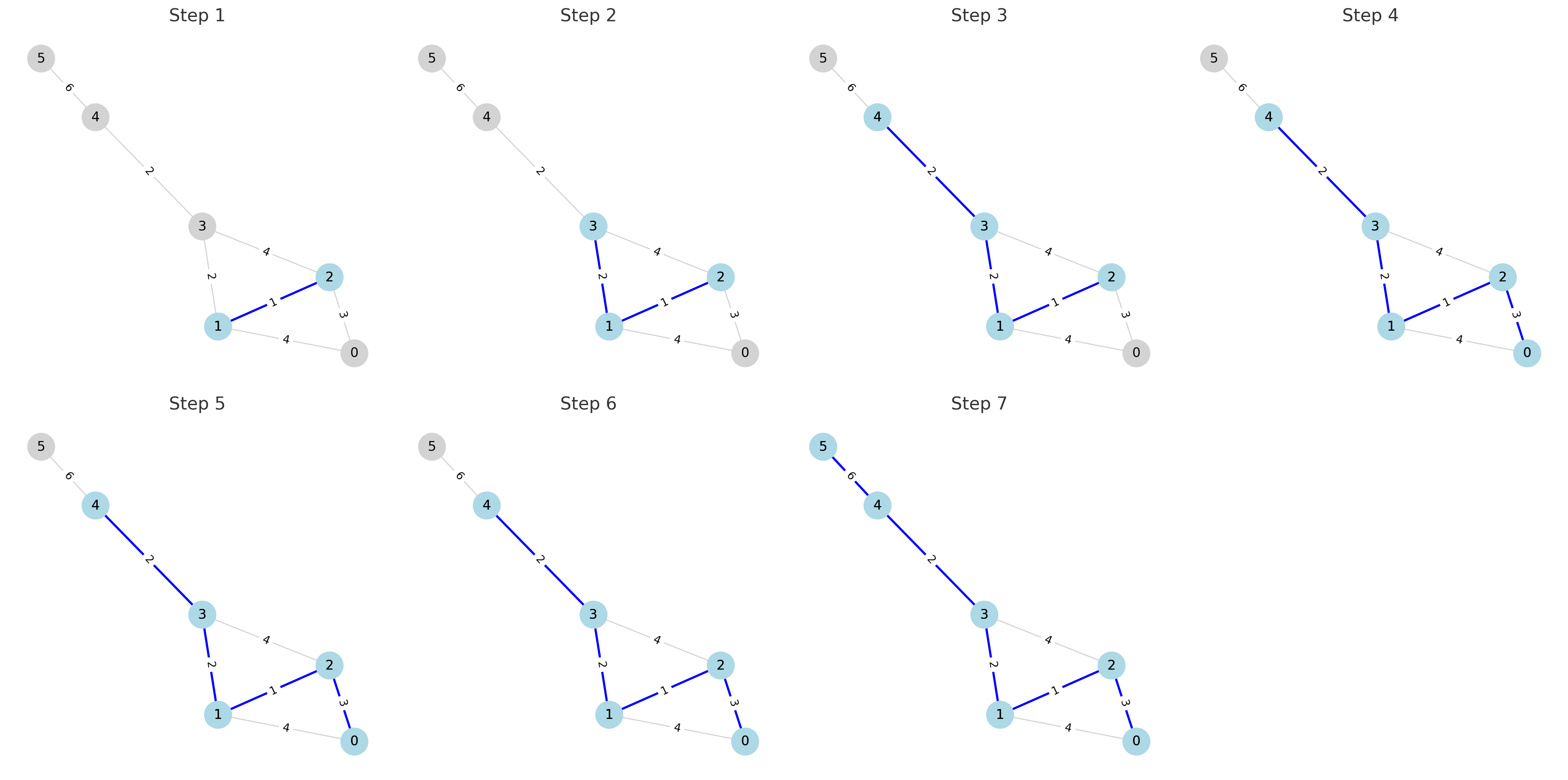
대략적으로 살펴보는 흐름은 이렇다.

1. 모든 간선을 가중치를 기준으로 정렬한다. ➡️ O(E log E)
2. 정렬한 간선을 순회하며 사이클이 생기지 않으면 선택한다. ➡️ O(E)
   • 이때 사이클 여부는 Union-Find를 통해 확인한다.

정렬이 전체 시간복잡도를 지배하므로 크루스칼 알고리즘의 시간복잡도는 O(E log E)가 된다.

⚽️ 자세한 흐름

위의 단계들을 하나하나 살펴보자.

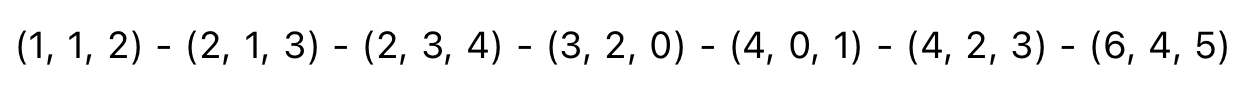
일단 간선을 (가중치, 노드A, 노드B) 와 같이 나타냈을 때, 위와 같이 정렬할 수 있다.

• Step 1
  

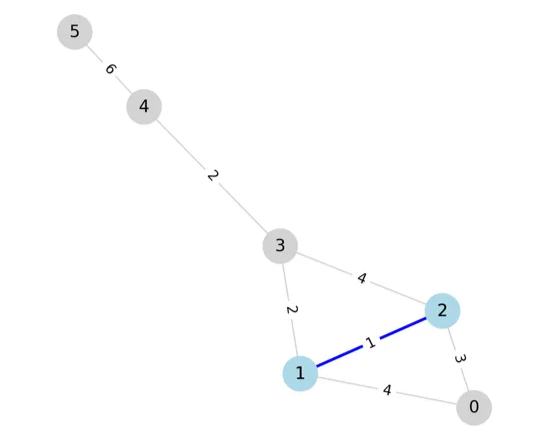
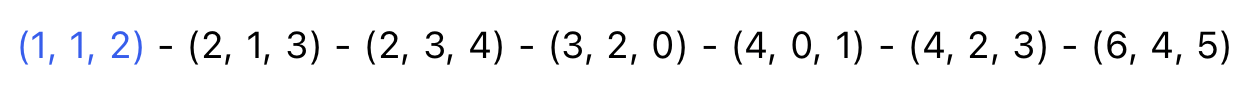
첫번째 간선의 노드 1과 2를 같은 그룹으로 묶어준다. 즉, 선택된(파란색으로 칠해진) 정점이 선택된 그룹에 있는 정점이 된다.
간선을 선택할 때 이미 두 정점 모두 선택된 그룹에 속해있다면 사이클을 형성하는 것으로 걸러낼 수 있다.
해당 간선을 선 사이클을 형성하지 않으므로 선택하고 다음으로 넘어간다.

• Step 2
  

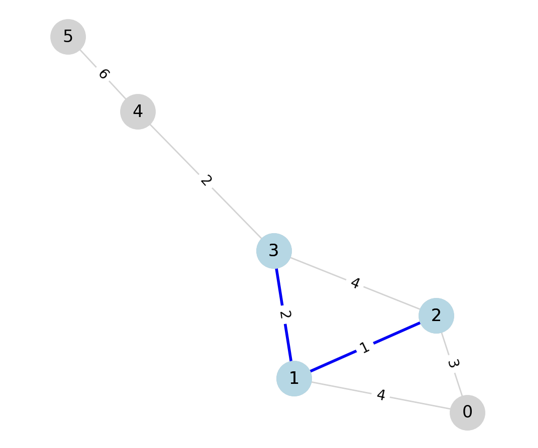
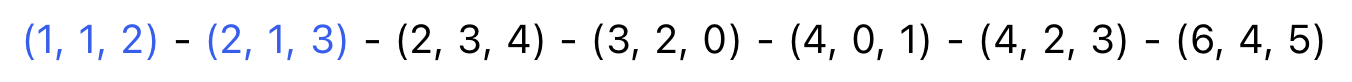
두번째 간선을 선택했을 때 3이 선택되지 않은 그룹의 정점이므로 사이클 형성이 되지 않고,
두번째 간선 또한 선택하고 넘어간다.

• Step 3
  

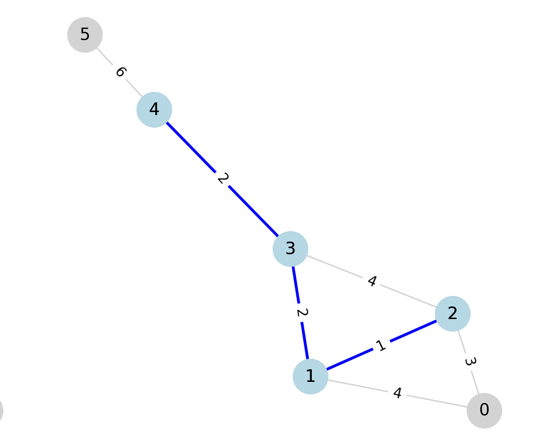
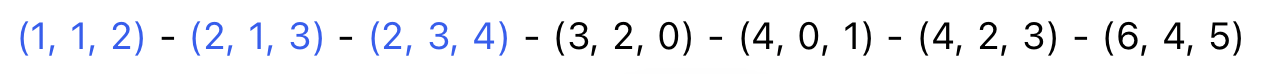
세번째 간선을 선택했을 때 4가 선택되지 않은 그룹의 정점이므로 사이클이 형성되지 않고,
선택하고 넘어간다.

• Step 4
  

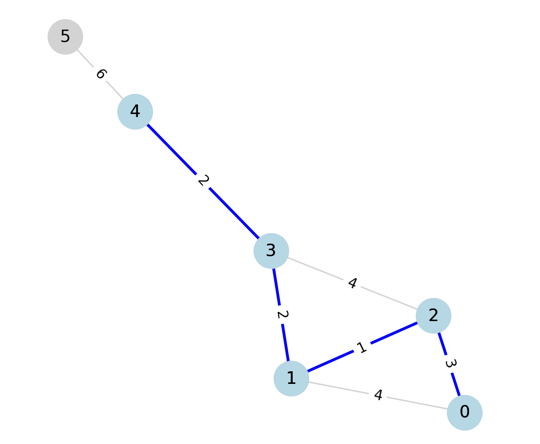
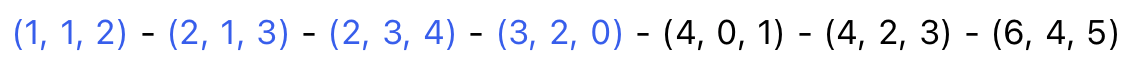
네번째 간선을 선택했을 때 0이 선택되지 않은 그룹의 정점이므로 사이클이 형성되지 않고,
선택하고 넘어간다.

• Step 5
  

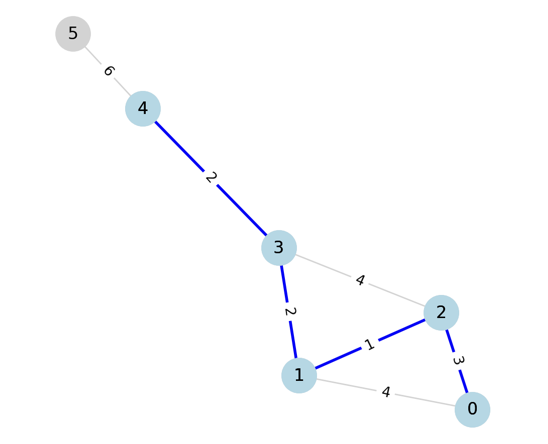
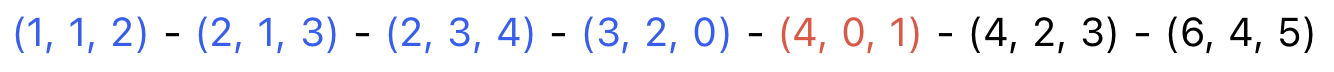
다섯번째 간선을 선택했을 때 1과 0 모두 선택된 그룹의 정점이므로 사이클이 형성되어,
선택하지 않고 넘어간다.

• Step 6
  

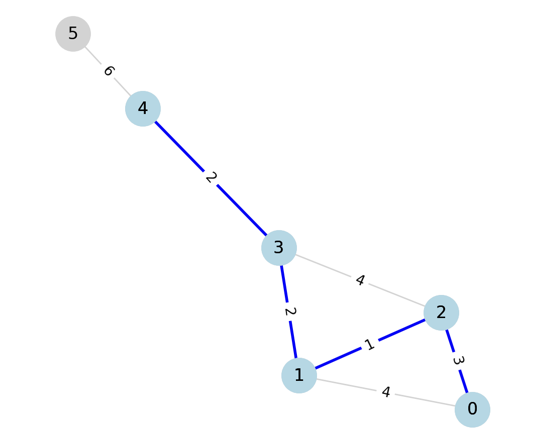
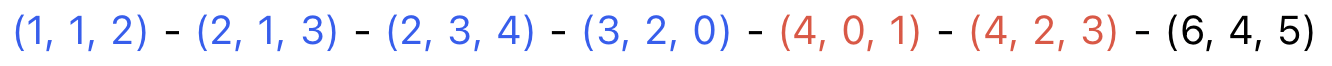
여섯번째 간선을 선택했을 때도 2와 3 모두 선택된 그룹의 정점이므로 사이클이 형성되어,
선택하지 않고 넘어간다.

• Step 7
  

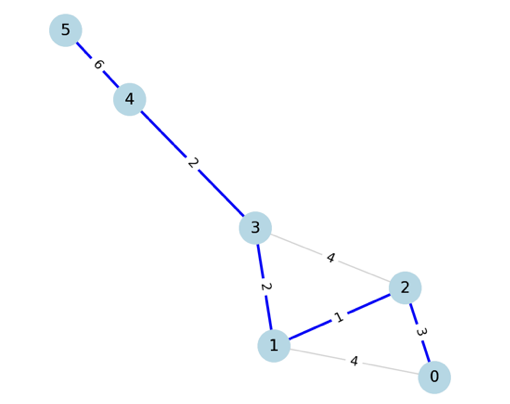
마지막으로 일곱번째 간선을 선택했을 때 5가 선택되지 않은 그룹의 정점이므로 사이클이 형성되지 않고,
선택하고 마무리한다.

⚽️ 코드 구현

### Kruskal
# union-find
def find_non_recursion(parent, x):
    while parent[x] != x:
        parent[x] = parent[parent[x]] # 경로 압축
        x = parent[x]
    return x

def find_recursion(parent, x):
		if parent[x] != x:
				parent[x] = find_recursion(parent, parent[x]) # 경로 압축
		return parent[x]

def union(parent, x, y):
    x_root = find(parent, x)
    y_root = find(parent, y)
    
    if x_root == y_root:
        return False
    parent[y_root] = x_root
    return True

# kruskal
def kruskal(v, graph):
    parent = [i for i in range(v+1)]
    graph.sort(key=lambda x: x[2])
    result = 0

    for a, b, weight in graph:
        if union(parent, a, b):
            result += weight
    return result

if __name__ == "__main__":
		v = 6
		inp = [(
    graph = [(1, 1, 2), (2, 1, 3), (2, 3, 4), (3, 2, 0), (4, 0, 1), (4, 2, 3), (6, 4, 5)]
    answer = kruskal(graph)
    print(answer)

🎱 Prim

프림 알고리즘은 정점을 중심으로 하는 MST 알고리즘이다.

⚽️ 핵심 개념

대략적인 흐름은 아래와 같다.

1. 초기 정점 pq에 삽입
   • 우선순위 큐(Priority Queue)를 사용해 노드 선택을 효율적으로 구현
   • 이 때 pq에는 가중치가 첫번째 인자로 오도록 (weight, node) 형식으로 삽입한다.
2. pq에서 pop한 정점이 방문하지 않았을 경우 방문처리 후 3번 진행
   • 방문했다면 사이클을 형성하게 되므로 선택하지 않음 → 4번 진행
3. 현재 정점과 연결된 모든 정점 중 방문하지 않은 정점을 pq에 삽입 ➡️ O(E log V)
4. 2번으로 돌아가 pq가 빌 때까지 반복 ➡️ O(E)

한 노드에 최대로 들어갈 수 있는 간선의 수는 전체 간선의 수인 E이고, 우선순위 큐를 이용해 삽입과 삭제를 구현했을 때 삽입, 삭제에 소요되는 시간은 최대 log V이므로 전체 시간복잡도는 O(E log V)이다.

⚽️ 자세한 흐름

위 단계들을 차례로 살펴보자.

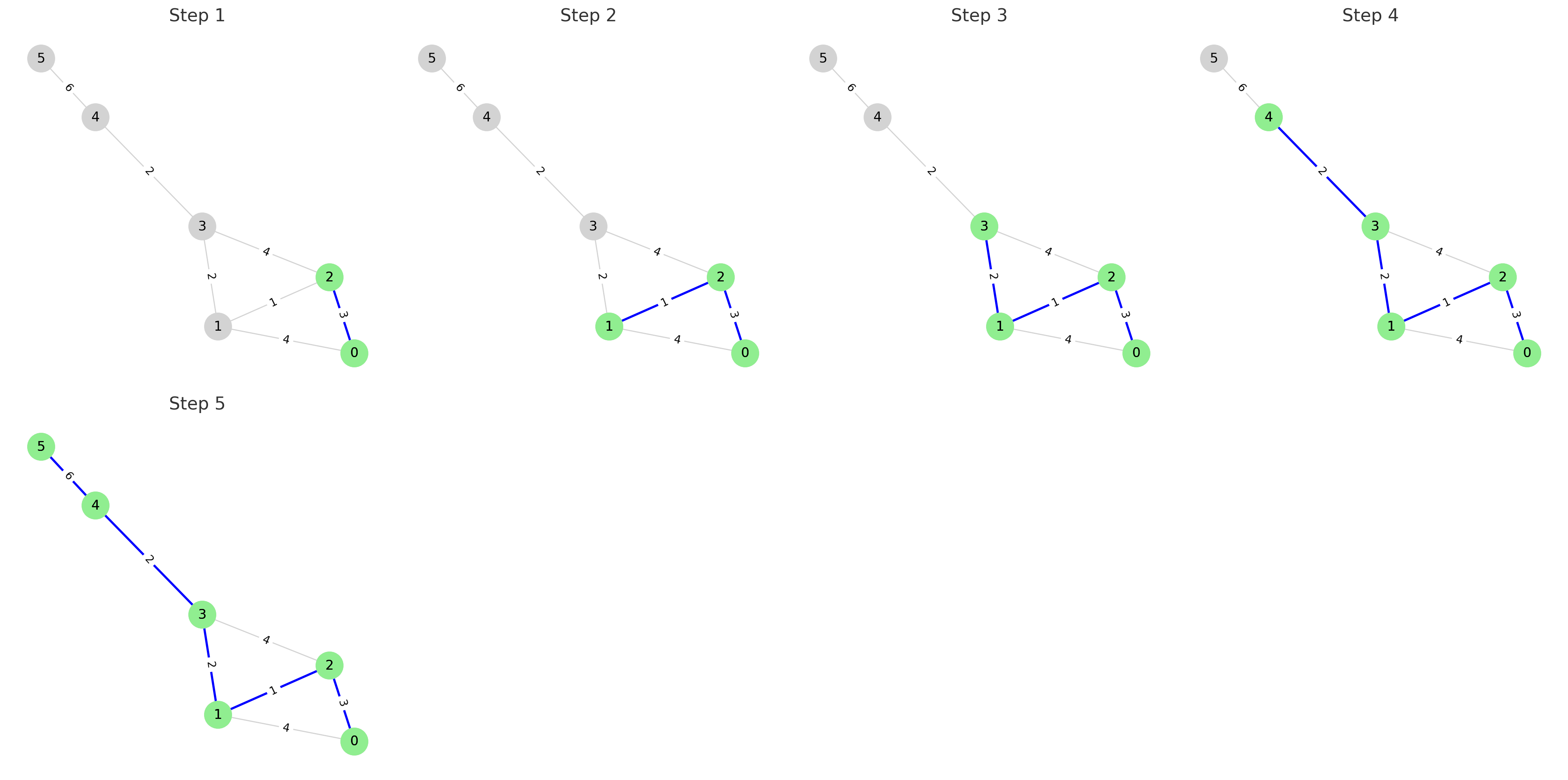
• Step 0 (초기 단계)
  

초기 노드를 0으로 설정하고, 0을 pq에 삽입한 뒤 시작한다. 이때 가중치는 0으로 설정한다.
pq에서 pop하면 초기값인 (0, 0)이 나오고, 초기에는 어떤 정점도 방문처리(초록색) 되지 않았으므로 0을 선택한다.
그리고 0과 연결된 정점인 1, 2 모두 방문하지 않은 정점이므로 pq에 push한다.

• Step 1
  

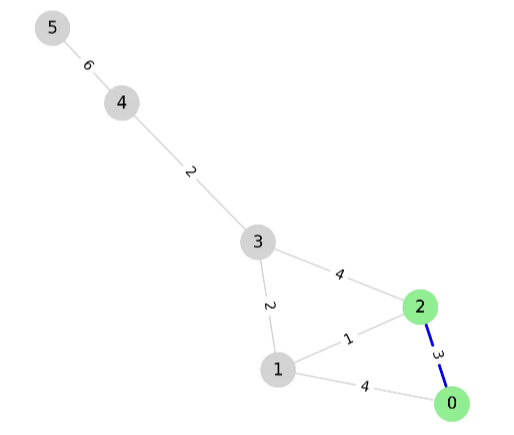
pq에서 pop하면 (3, 2)가 나오고, 2는 방문하지 않은 정점이므로 선택하고 방문처리한다.
2와 연결된 0, 1, 3 중에서 방문하지 않은 정점인 1, 3을 pq에 push한다.

• Step 2
  

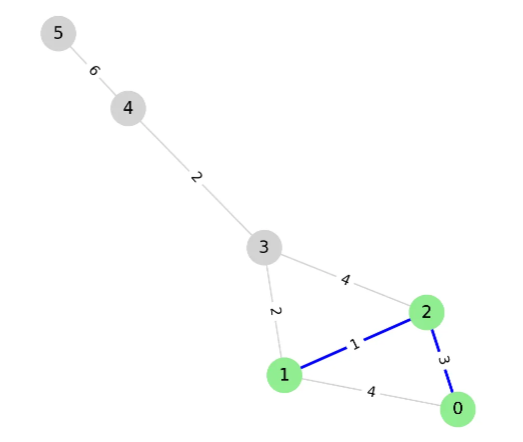
pq에서 pop하면 (1, 1)이 나오고, 1은 방문하지 않은 정점이므로 선택하고 방문처리한다.
1과 연결된 0, 2, 3 중에서 방문하지 않은 정점인 3을 pq에 push한다.

• Step 3
  

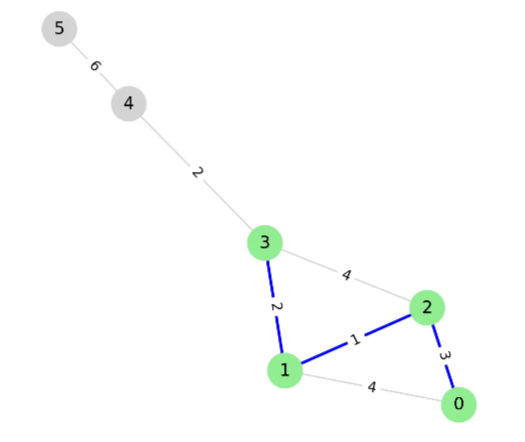
pq에서 pop하면 (2, 3)이 나오고, 3은 방문하지 않은 정점이므로 선택하고 방문처리한다.
3과 연결된 1, 2, 4 중에서 방문하지 않은 정점인 4를 pq에 push한다.

• Step 4
  

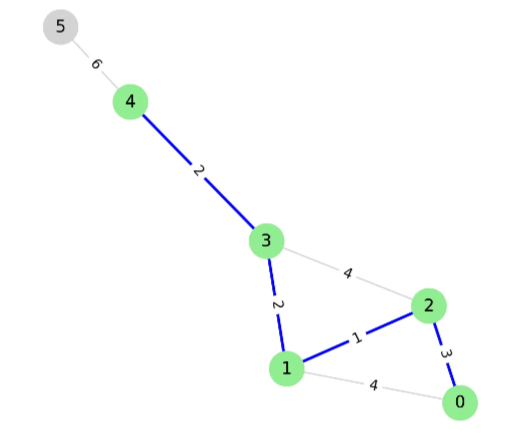
pq에서 pop하면 (2, 4)가 나오고, 4는 방문하지 않은 정점이므로 선택하고 방문처리한다.
4와 연결된 3, 5 중에서 방문하지 않은 정점인 5를 pq에 push한다.

• Step 5

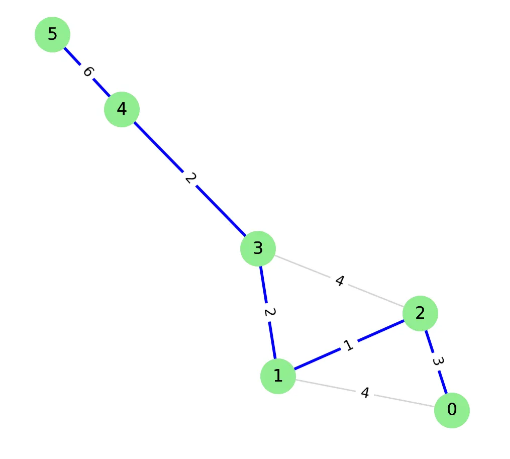
pq에서 pop하면 (4, 1)이 나오지만 1은 방문한 정점이므로 선택하지 않는다.
다시 pop하면 (4, 3)이 나오지만 3 또한 방문한 정점이므로 선택하지 않는다.
다시 pop하면 (6, 5)가 나오고, 5는 방문하지 않은 정점이므로 선택하고 방문처리한다.
5와 연결된 4는 방문한 정점이므로 아무것도 push하지 않는다.

pq가 비었으므로 반복문을 종료한다.

⚽️ 코드 구현

import heapq
from collections import defaultdict
### Prim
def prim(graph):
    v = len(graph)
    visited = [0 for _ in range(v+1)]
    pq = []

    # initial setting
    heapq.heappush(pq, (0, 1))
    result = 0

    # repitition
    while pq:
        weight, x = heapq.heappop(pq)

        if visited[x]:
            continue

        visited[x] = 1
        result += weight

        for nx, weight in graph[x]:
            if not visited[nx]:
                heapq.heappush(pq, (weight, nx))
    return result

🎱 어떤 차이점이 있을까?

	Kruskal (non-recursion)	Kruskal (recursion)	Prim
기준	간선	간선	노드
사이클 방지 방식	Union-Find (non-recursion)	Union-Find (recursion)	visited 배열
사용 자료구조	정렬 + Union-Find	정렬 + Union-Find	Priority Queue
사용 상황	정점에 비해 간선이 많은 경우	정점에 비해 간선이 많은 경우	간선에 비해 정점이 많은 경우
시간복잡도	O(E log E)	O(E log E)	O(E log V)
주의사항	❌	재귀 깊이 제한에 주의	❌

간단하게 테이블을 통해 차이점을 정리해봤다.
나같으면 웬만하면 Kruskal 알고리즘을 사용할 것 같긴 하다.