Algorithm - 기본 용어와 검색 알고리즘

Algorithm

• 문제를 해결할 수 있는 잘 정의된(well defined) 유한(finite) 시간 내에 종료되는 계산적인 절차
• 입력을 받아서 출력으로 전환시켜주는 일련의 계산절차
• 계산과 데이터 처리에 사용되는 일련의 명령들
• 상태 변화는 반드시 결정적인 것은 아니다. 확률적 알고리즘과 같은 알고리즘은 무작위성을 포함한다.

알고리즘의 표기

자연어

• 문제를 정확하게 기술하는 것에 있어 어려움이 있다.
• 상대적으로 긴 문장이 필요하다.
• 사람에 따라 다르게 해석할 여지가 존재한다.

프로그래밍 언어

• 구체적인 기술을 해야하므로 알고리즘을 이해하는 것에 있어 어려움이 생긴다.

pseudo code

• 직접 실행 가능한 프로그래밍 언어는 아니지만, 실제 프로그램에 가깝게 계산과정을 표현할 수 있는 언어
• 간결하면서도 정확한 의미 표현이 가능하다.

순차검색 알고리즘(Sequential search)

• 대상 아이템을 찾을 때까지 배열에 있는 모든 아이템을 차례로 검사한다.
• 아이템을 찾는다면 배열에서의 인덱스를 반환하고 찾이 못한다면 0을 반환한다.

pseudo code

C++

#include <iostream>
using namespace std;

void main()
{
    int arr[10] = { 1, 3, 5, 17, 23, 45, 92, 120, 230, 493 };
    int num;
    cout << "input num : ";
    cin >> num;

    for (int i = 0; i < 10; i++)
    {
        if (arr[i] == num)
        {
            cout << "Find Index : " << i << endl;
            return;
        }
    }
    cout << "Not Found" << endl;
}

python

def sequentual_search(arr, x):
    n = len(arr)  # 입력 크기 n
    location = 0
    for location in range(n):
        if x == arr[location]:
            return location
        location += 1
    if location == n:
        return 0

arr = [1, 3, 5, 17, 23, 45, 92, 120, 230, 493]
print(sequentual_search(arr, 23))
print(sequentual_search(arr,2))

이분검색 알고리즘

• 한 번의 검색마다 검색 대상의 총 크기를 반씩 감소시키며 검사를 진행한다.
• 정렬된 데이터에 사용한다.
• 최악의 경우에도 lg(n) + 1번의 검사만을 진행하면 된다.

pseudo code

c++

#include <iostream>
using namespace std;

/*
검색 대상이 배열 내에 존재한다면 index 반환
검색 대상이 배열 내에 존재하지 않는다면 -1을 반환한다.
*/
int BinarySearch_a(int array[], int sizeOfArray, int value) {
    int midPoint;
    int first = 0;
    int last = (sizeOfArray - 1);
    bool moreToSearch = (first <= last);
    bool found = false;
    int Pos = -1;
    while (moreToSearch && !found) {
        midPoint = (first + last) / 2;
        if (array[midPoint] > value) {
            last = midPoint - 1;
            moreToSearch = (first <= last);
        }
        else if (array[midPoint] < value) {
            first = midPoint + 1;
            moreToSearch = (first <= last);
        }
        else {
            found = true;
            Pos = midPoint;
            break;
        }
    }
    if (!found)
        Pos = -1;
    return Pos;
}

/*
찾고자 하는 값보다 작거나 같은 값 중에서 가장 큰 값을 반환한다.
*/
int BinarySearch_b(int array[], int sizeOfArray, int value) {
    int midPoint;
    int first = 0;
    int last = (sizeOfArray - 1);
    bool moreToSearch = (first <= last);
    bool found = false;
    int Pos = -1;
    while (moreToSearch && !found) {
        midPoint = (first + last) / 2;
        if (array[midPoint] > value) {
            last = midPoint - 1;
            moreToSearch = (first <= last);
        }
        else if (array[midPoint] < value) {
            first = midPoint + 1;
            moreToSearch = (first <= last);
        }
        else {
            found = true;
            Pos = midPoint;
            break;
        }
    }
    if (!found)
        Pos = last;
    return array[Pos];
}

/*
찾고자 하는 값보다 크거나 같은 값들 중에서 가장 작은 값을 반환한다.
*/
int BinarySearch_c(int array[], int sizeOfArray, int value) {
    int midPoint;
    int first = 0;
    int last = (sizeOfArray - 1);
    bool moreToSearch = (first <= last);
    bool found = false;
    int Pos = -1;
    while (moreToSearch && !found) {
        midPoint = (first + last) / 2;
        if (array[midPoint] > value) {
            last = midPoint - 1;
            moreToSearch = (first <= last);
        }
        else if (array[midPoint] < value) {
            first = midPoint + 1;
            moreToSearch = (first <= last);
        }
        else {
            found = true;
            Pos = midPoint;
            break;
        }
    }
    if (!found)
        Pos = first;

    return array[Pos];
}

int main()
{
    int arr[10] = { 1, 3, 5, 17, 23, 45, 92, 120, 230, 493 };
    int result, result2, result3, result4;
    result = BinarySearch_a(arr, 10, 23);
    result2 = BinarySearch_a(arr, 10, 6);
    result3 = BinarySearch_b(arr, 10, 22);
    result4 = BinarySearch_c(arr, 10, 46);
    cout << result << " " << result2 << " " << result3 << " " << result4;
}

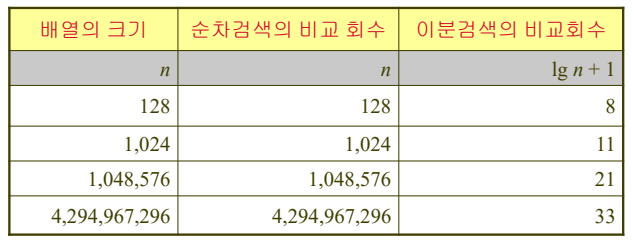
순차검색 vs. 이분검색

• 최악의 경우

피보나치 수(재귀적 방법)

• 피보나치 수를 구하는 과정은 재귀 알고리즘을 사용하면 같은 수를 중복 계산하기 때문에 수행속도가 매우 느리다.

함수 호출 횟수

T(n) = fib(n)을 계산하기 위하여 fib함수를 호출하는 횟수

T(0) = 1, T(1) = 1
T(n) = T(n-1) + T(n - 2) + 1 for n>= 2

T(n) > 2T(n - 2) > 4T(n-4) > 8T(n-6) ... > 2^(n/2)T(0) = 2^(n/2) 

pseudo code

C++

int Fibo(int n) {
    if (n <= 1)
        return n;
    else
        return Fibo(n - 1) + Fibo(n - 2);
}

python

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

피보나치수 (반복적 방법)

• 반복적 방법을 이용하여 계산하면 중복계산이 없기 때문에 수행속도가 훨씬 빠르다.
• 계산하는 항의 총 개수 T(n) = n + 1

pseudo code