알고리즘의 분석
- 일반적으로 공간복잡도는 추가적인 기기의 부착으로 해결이 가능하기에 시간복잡도에 대한 관심도가 더 높다.
공간복잡도 분석
- 입력크기에 따라서 작업공간(메모리)이 얼마나 필요한지 결정하는 절차
시간복잡도 분석
- 입력 크기에 따라 단위연산이 몇 번 수행되는지 결정하는 절차
- 알고리즘이 수행되는 기계에 따라 문제를 해결하는 시간이 달라진다.
시간복잡도 분석의 기준
- 기계에 독립적인, 문제 본연의 복잡도로 표현한다.
표현 척도
- 단위 연산 (비교문, 지정문 etc.)
- 입력 크기 (배열의 크기, 리스트의 길이, 트리에서의 마디와 이음선의 수 etc.)
분석 방법의 종류
모든 경우 분석
- 입력 크기에만 종속하며 입력값과는 무관하다.
- 입력 값과는 무관하게 결과값은 항상 일정하다.
최악의 경우 분석
- 입력 크기와 입력값 모두에 종속한다.
- 단위연산이 수행되는 횟수가 최대인 경우를 선택한다.
평균의 경우 분석
- 입력 크기에 종속한다.
- 모든 입력에 대해서 단위연산이 수행되는 기대치(평균)
- 각 입력에 대해서 확률 할당 가능
- 일반적으로 최악의 경우 계산보다 계산이 복잡하다.
배열 덧셈의 시간복잡도 분석
pseudo code

단위 연산 : 덧셈
- 배열 내용에 상관 없이 for루프가 n번 반복되며 각 루프마다 덧셈이 1회 수행된다.
- 배열의 크기 n에 대해서 총 T(n) = n 수행된다.
단위연산 : 지정문
- 배열 내용에 상관 없이 for루프가 n번 반복된다.
- 초기 result의 값을 지정하며 각 루프마다 i와 result를 지정하기 때문에 총 T(n) = 2n + 1번 수행된다.
교환 정렬의 시간 복잡도 분석
pseudo code

단위연산 : 조건문(S[j]와 S[i]의 비교)
- j-루프가 수행될 때마다 조건문 1번씩 수행한다.
- 조건문의 총 수행회수
| i | j-loop 수행횟수 |
|---|---|
| 1 | n-1 |
| 2 | n-2 |
| 3 | n-3 |
| ... | ... |
| n-1 | 1 |
- 따라서 T(n) = (n-1) + (n-2) ... + 1 = (n-1)n / 2
단위 연산 : 교환연산 (exchange S[i] and S[j])
- 최악의 경우로는 입력 배열이 거꾸로 정렬되어 있는 경우이며 W(n) = n(n-1) / 2 번 수행된다.
순차검색 시간복잡도 분석
단위연산 : 배열의 아이템과 키 값의 비교 연산 (최선의 경우)
- 최선의 경우에는 입력의 크기에 상관 없이 단위연산이 1번만 수행되는 경우이다.
- B(n) = 1
단위연산 : 배열의 아이템과 키 값의 비교 연산 (최악의 경우)
- 최악의 경우에는 키가 배열의 마지막 아이템이거나 배열에 없는 경우를 의미한다.
- 따라서 비교 연산이 n번 수행되며 W(n) = n이다.
단위연산 : 배열의 아이템과 키 값의 비교 연산 (평균의 경우)
배열의 아이템이 모두 다르다고 가정하며 키값이 배열 안에 존재한다고 고려하는 경우
- 키 x가 배열 안의 k번째에 있을 확률은 각각 1/n이다.
- x가 k번째에 존재한다면 이를 찾기위하여 수행하는 단위연산의 홧수는 k번이다.
- 따라서
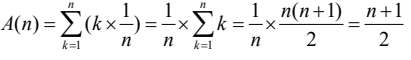
x가 배열에 없는 경우도 고려하는 경우
- x가 배열 안에 있을 확률을 p라고 한다면, x가 배열의 k번째 있을 확률은 p/n, 배열에 없을 확률은 1-p이다.

복잡도 함수의 표현
big - O 표기법
-
정의 : 점근적 상한(asymptotic upper bound)
-
주어진 복잡도 함수 f(n)에 대해서 g(n)∈Ο(f(n)) 이면 n ≥ N인 모든 정수 n에 대해서 0 ≤ g(n) ≤ c × f(n)이 성립하는 양의 실수 c와 음이 아닌 정수 N이 존재한다.
-
O(f(n)) = {g(n): there exist positive constants c and N such that 0≤ g(n) ≤ c× f(n) for all n ≥ N}
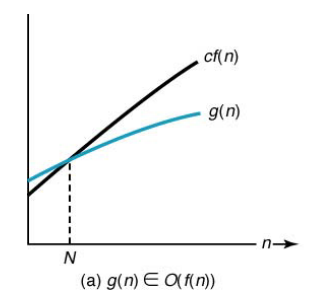
-
어떤 알고리즘의 시간복잡도가 O(f(n))이라면 입력의 크기 n에 대해서 알고리즘의 수행시간이 아무리 늦어도 c*f(n)은 된다는 것을 보장한다.
Ω표기법
- 정의 : 점근적 하한(asymptotic lower bound)
- 주어진 복잡도 함수 f(n)에 대해서 g(n) ∈ Ω(f(n))이면 n ≥ N인 모든 정수 n에 대해서 g(n) ≥ c × f(n) ≥ 0이 성립하는 양의 실수 c와 음이 아닌 정수 N이 존재한다.
- Ω(f(n)) ={g(n): there exist positive constants c and N such that g(n) ≥ c × f(n) ≥ 0 for all n ≥ N}
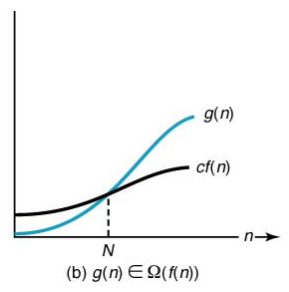
- 어떤 알고리즘의 시간복잡도가 Ω(f(n))이라면 입력의 크기 n에 대해서 알고리즘의 수행시간이 아무리 빨라도 c*f(n)밖에 되지 않음을 의미한다. (절대로 더 빠를 수는 없다)
Θ 표기법
- 정의 : (asymptotic tight bound)
- 복잡도 함수 f(n) 에 대해서 Θ(f(n))= O(f(n))∩ Ω(f(n))
- n ≥ N 인 모든 정수 n 에 대해서 c × f(n) ≤ g(n) ≤ d × f(n)이 성립하는 양의 실수 c와 d, 음이 아닌 정수 N이 존재한다.
- Θ(f(n))={g(n): there exist positive constants c, d, and N such that c × f(n) ≤ g(n) ≤ d × f(n) for all n ≥ N}
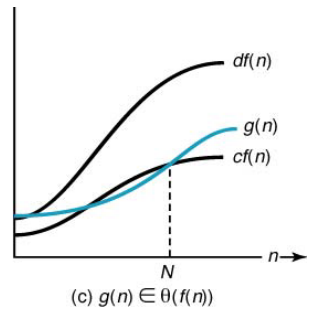
small - O 표기법
- small o는 복잡도 함수끼리의 관계를 나타내기 위한 표기법이다.
- 주어진 복잡도 함수 f(n)에 대해서 g(n) ∈ o(f(n))이면 모든 양의 실수 c에 대해, n ≥ N인 모든 n 에 대해서 0 ≤ g(n) ≤ c × f(n) 이 성 립하는 음이 아닌 정수 N 이 존재한다.
- o(f(n))={g(n): for any positive constants c>0, there exists a constant N>0 such that 0 ≤ g(n) ≤ c × f(n) for all n ≥ N}
big-O vs. small-O
- big-O는 실수 c > 0 중에서 하나만 성립하여도 된다.
- small-O는 모든 c>0에 대하여 성립하여야 한다.
